ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6743
Скачиваний: 28

96
переменные x, z- связанные, y, v- свободные.
Мы рассмотрели предикаты, значения которых (истина или
ложь) известны для каждого набора значений свободных предмет-
ных переменных. Такие предикаты называются определенными
предикатами. Но существуют еще так называемые переменные
предикаты, для которых значения не определены. Будем обозна-
чать переменные предикаты большими буквами латинского алфави-
та:
X, Y,.., X
1
, X
2
,.., W(x
1
, x
2
,.., x
n
), V(x
1
, x
2
,.., x
n
), …
Переменный предикат от нуля переменных есть переменное выска-
зывание. Применяя к переменным предикатам операции ٧ , ٨ ,
→, ⎯,
~,
∃, ∀, получим формулы логики предикатов. Так, выражение
∀x W (x, y) ٧ x → U (z)
– пример формулы логики предикатов.
3.8.2
Равносильные
формулы
логики
предикатов
Рассматривая формулы логики предикатов над полем М можно
говорить о формулах, равносильных над данным полем, то есть о
таких формулах, которые принимают одно и то же значение при
замене всех свободных предметных переменных предметами и всех
переменных предикатов
− определенными.
Пример. Рассмотрим формулы
∀x W (x) и ∃x W (x) над полями
М
1
= {a} и М
2
= {a, b}.
Пусть
∀x W (x) и ∃x W (x) даны над полем М
1
, Значениями пе-
ременного предиката W (x) могут быть два определенных предиката
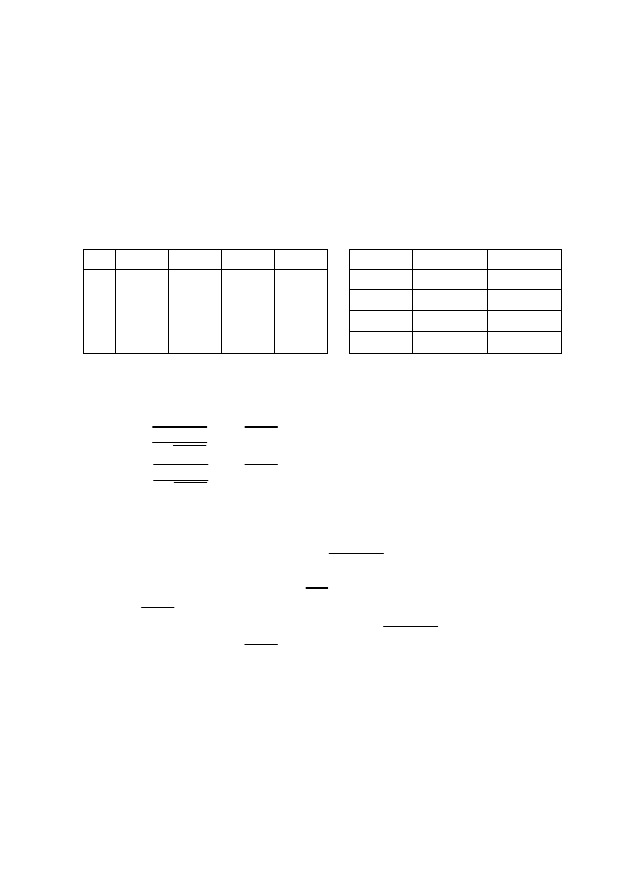
A(x) и B(x) (табл. 3.13). Составим истинностную таблицу формул
(табл. 3.14).
Таким образом, формулы
∀x W (x) и ∃x W (x) равносильны над
полем M
1
.
Таблица 3.13 – Предикаты над М
1
Таблица 3.14 – Равносильность над М
1
x
A (x)
B (x)
W (x)
∀x W (x)
∃x W (x)
A (x)
0
0
a 0 1
B (x)
1
1
97
Пусть теперь формулы
∀x W (x) и ∃x W (x) даны над полем М
2
.
В качестве значений переменного предиката W (x) нужно взять оп-
ределенные предикаты над полем М
2
. Таких предикатов существует
четыре (табл.3.15). Составив истинностную таблицу формул
∀x W (x) и ∃x W (x) (табл.3.16), убеждаемся в их неравносильности
над полем М
2
.
Таблица 3.15- Предикаты над М
2
Таблица 3.1- Неравносильность над М
2
x I
1
(x)
I
2
(x)
I
3
(x)
I
4
(x)
W (x)
∀x W (x) ∃x W (x)
I
1
(x)
0
0
a
0 0 1 1
I
2
(x) 0
1
I
3
(x) 0
1
b
0 1 0 1
I
4
(x) 1
1
Формулы логики предикатов называются равносильными, ес-
ли они равносильны над любым полем.
Примеры равносильных формул:
1)
∀x W (x) и ∃x W (x);
2)
∀x W (x) и ∃x W (x);
3)
∃x W (x) и ∀x W (x);
4)
∃x W (x) и ∀x W (x).
Докажем равносильность первой пары формул. Пусть М – про-
извольное поле, а A (x) – некоторый определенный предикат над
ним. Подставим вместо переменного предиката W (x) определенный
предикат A (x). Пусть высказывание
∀x A (x) истинное, тогда выска-
зывание
∀x A(x) ложно. Следовательно, существует предмет a из
поля M, что A (a) ложно, тогда A (a) – истинно. Значит, высказыва-
ние
∃x A (x) истинно. Аналогичными рассуждениями получим, что
из предположения ложности высказывания
∀x A (x) следует лож-
ность высказывания
∃x A (x).
Среди всех формул логики предикатов можно выделить фор-
мулы, истинные над любым полем, их называют тождественно-
истинными. Например, формула
∀x W(x) → ∃x W(x) является тож-
дественно-истинной.
В общем случае выяснить вопрос, является ли данная формула
тождественно-истинной, сложно, так как приходится использовать
понятие бесконечности.

98
3.9
Задачи
и
упражнения
1.
Дано высказывание А: «Существуют четные простые числа».
Определите, истинно оно или ложно. Укажите среди следующих
высказываний отрицание высказывания А: а) «Существуют не-
четные простые числа»; б) «Неверно, что существуют четные
простые числа»; в) «Любое простое число нечетно».
2.
Для высказывания А: «Любые два треугольника подобны» сфор-
мулируйте отрицание и двойное отрицание. Какие из этих трех
высказываний истинны?
3.
Даны высказывания «Я купил велосипед» (А); «Я путешествовал
по России» (В) и «Я участвовал в соревнованиях по велосипеду»
(С). Сформулируйте высказывания, соответствующие формулам:
А ٨ В, А ٨ В ٨ С, А ٨
⎯С, А ٨ В, ⎯В ٨⎯С.
4.
Даны высказывания «Четырехугольник MNPQ – параллело-
грамм» (А) и «Диагонали четырехугольника MNPQ в точке пере-
сечения делятся пополам» (В). Сформулируйте высказывания,
соответствующие формулам А
→ В, В → А, ⎯А, ⎯В, ⎯А → В,
⎯В → А.
5.
Составьте таблицы истинности для следующих формул:
X
→ (Y ٧ Z), (X → Y) ٧ (X → Z).
6.
Покажите, что формулы X ٨Y
∼ Y ٨ X, X ٧Y∼Y ٧X,
((X
→ Y) ٨ X) → Y являются тавтологиями.
7.
Докажите равносильность формул:
а) X ٨ (Y ٧ Z) и (X ٨ Y) ٧ (X ٨ Z);
б) X ٧ (Y ٨ Z) и (X ٧ Y) ٨ (X ٧ Z);
в) X ٧ Y и
⎯X ٨⎯Y;
г) X ٨ Y и
⎯X ٧⎯Y;
д) X
→ (Y → Z) и (X ٨ Y) → Z;
е) (X
→ Y) ٨ (X → Z) и X → (Y ٨ Z).
8.
Постройте совершенные ДНФ и КНФ функций:
x
1
⊕ x
2
, x
1
↓ x
2
, x
1
→ x
2
, x
1
∼ x
2
.
9.
Запишите в совершенных ДНФ и КНФ булеву функцию
f
1
(x
1
, x
2
, x
3
), принимающую значение 1 на наборах с номерами
0, 3, 7. Определите, к каким классам функций относится эта
функция.
10.
Проверьте справедливость равенств: x =
⎯x ⊕ 1, x
1
→ x
2
=
=
⎯x
1
٧ x
2
.

99
11.
Составьте таблицу свойств булевых функций двух переменных.
Из таблицы выпишите все полные системы булевых функций.
12.
Проверьте линейность булевой функции f
2
(x
1
, x
2
, x
3
), прини-
мающей значение 1 на наборах с номерами 0, 1, 5, 6.
13.
Синтезируйте логические схемы булевых функций из задач № 9,
12 в базисах: а) { ٧,
⎯ }; б) { ٨,⎯ }.
14.
Найдите минимальную ДНФ функции f (x
1
, x
2
, x
3
, x
4
), прини-
мающей значение 1 на наборах с номерами 0, 1, 2, 5, 6. 7, 8, 12,
13.
15.
Приведите примеры: а) монотонной функции, которая одновре-
менно была бы линейной; б) самодвойственной функции, кото-
рая одновременно была бы линейной; в) линейной и монотонной
функций.
16.
Покажите, что функции Шеффера и Вебба не являются ни ли-
нейными, ни монотонными, ни самодвойственными.
17.
Докажите полноту системы булевых функций, состоящей из
дизъюнкции, константы 0 и эквивалентности.
18.
Путешественник попал к людоедам. Они разрешают ему произ-
нести какое-нибудь высказывание и ставят условие, что если его
высказывание будет истинным, то его сварят, а если ложным, то
зажарят. Какое высказывание следует произнести путешествен-
нику, чтобы избежать гибели?

100
МЕТОДИЧЕСКИЕ
УКАЗАНИЯ
ПО
КУРСУ
«
ДИСКРЕТНАЯ
МАТЕМАТИКА
»
для специальностей 220400 и 071900
В процессе изучения дисциплины студенту следует выполнить
четыре контрольных работы (две во втором и две в третьем семест-
ре). Номер варианта выбирается по общим правилам, в соответствии
с шифром студента. Оформление КР – стандартное: каждая работа
должна содержать титульный лист, в поясняющем тексте следует
привести формулировку каждого задания и подробное описание ре-
шения задачи, а также список использованной литературы.
Выполненная КР, высылается в адрес ТМЦ ДО обычной или
электронной почтой.
Контрольная
работа
№
1
Темой данной КР является теория множеств. Каждая работа
содержит шесть заданий из различных разделов теории множеств.
Некоторые задания повторяются в различных вариантах. В первом
задании приведены ссылки на номера задач данного учебного посо-
бия.
При выполнении КР особое внимание следует обратить на за-
дания, связанные с доказательством тождеств. Нужно помнить, что
иллюстрация тождества с помощью диаграмм Эйлера не является
его доказательством. Доказательство должно быть проведено путем
логических рассуждений.
В качестве примера рассмотрим доказательство тождества
(A U B) ∩ C = (A ∩ C) U (B ∩ C),
представляющего собой свойство дистрибутивности операций объе-
динения и пересечения. Чтобы доказать это тождество,
надо показать, что множество (A U B) ∩ C равно множеству
(A ∩ C) U (B ∩ C), т.е. что каждый элемент первого множества яв-
ляется элементом второго множества, и наоборот.
Пусть x
∈ (A U B) ∩ C. Докажем, что x ∈ (A ∩ C) U (B ∩ C).
Так как x принадлежит пересечению множества A U B с множест-
вом С, то x
∈ AUB и x ∈ С. Из того, что x ∈ A U B, следует, что