ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16675
Скачиваний: 202

91
Буквы, под которыми находятся нули, инвертируем и получаем искомое
выражение:
.
D
C
B
A
f =
Если построить таблицу соответствия для этой функции, то в колонке f
будет записана только одна единица – в строке с номером 5. Это десятичный
номер набора 0101.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Функции, которые принимают единичное значение только на
одном наборе, имеют в булевой алгебре важнейшее значение, по-
этому получили специальное наименование и обозначение. Называ-
ют их минимальными термами, а коротко –
минтéрмами
[4; 48].
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
У минтермов существует и определение: минтермом n аргументов назы-
вается такая конъюнкция их, в которую каждый аргумент входит один раз в
прямой или инверсной форме [48].
Обозначаются минтермы буквой m с десятичным индексом, являющимся
номером минтерма. Двоичный эквивалент номера минтерма – это набор, на ко-
тором минтерм равен единице. Рассмотрим, например, минтерм трёх перемен-
ных с номером 6. Двоичный эквивалент числа шесть имеет вид 110. На этом
наборе минтерм m
6
равен единице. Следовательно,
.
6
C
AB
m
=
Минтермы обладают свойством: конъюнкция любых двух различных
минтермов, зависящих от одних и тех же аргументов, тождественно равна ну-
лю. Это следует из того, что два минтерма могут отличаться только инверсиями
аргументов, т. е. если минтермы не равны, то всегда найдётся переменная, ко-
торая в один минтерм входит в прямой форме, а в другой – с отрицанием,
конъюнкция которых равна нулю. Например, если n = 4, то
.
0
5
12
=
⋅
=
⋅
D
C
B
A
D
C
B
A
m
m
Если таблица соответствия содержит только одну единицу в колонке f, то
функция представляет собой минтерм. Если же в колонке f содержится не-
сколько единиц, то функцию образует дизъюнкция соответствующих минтер-
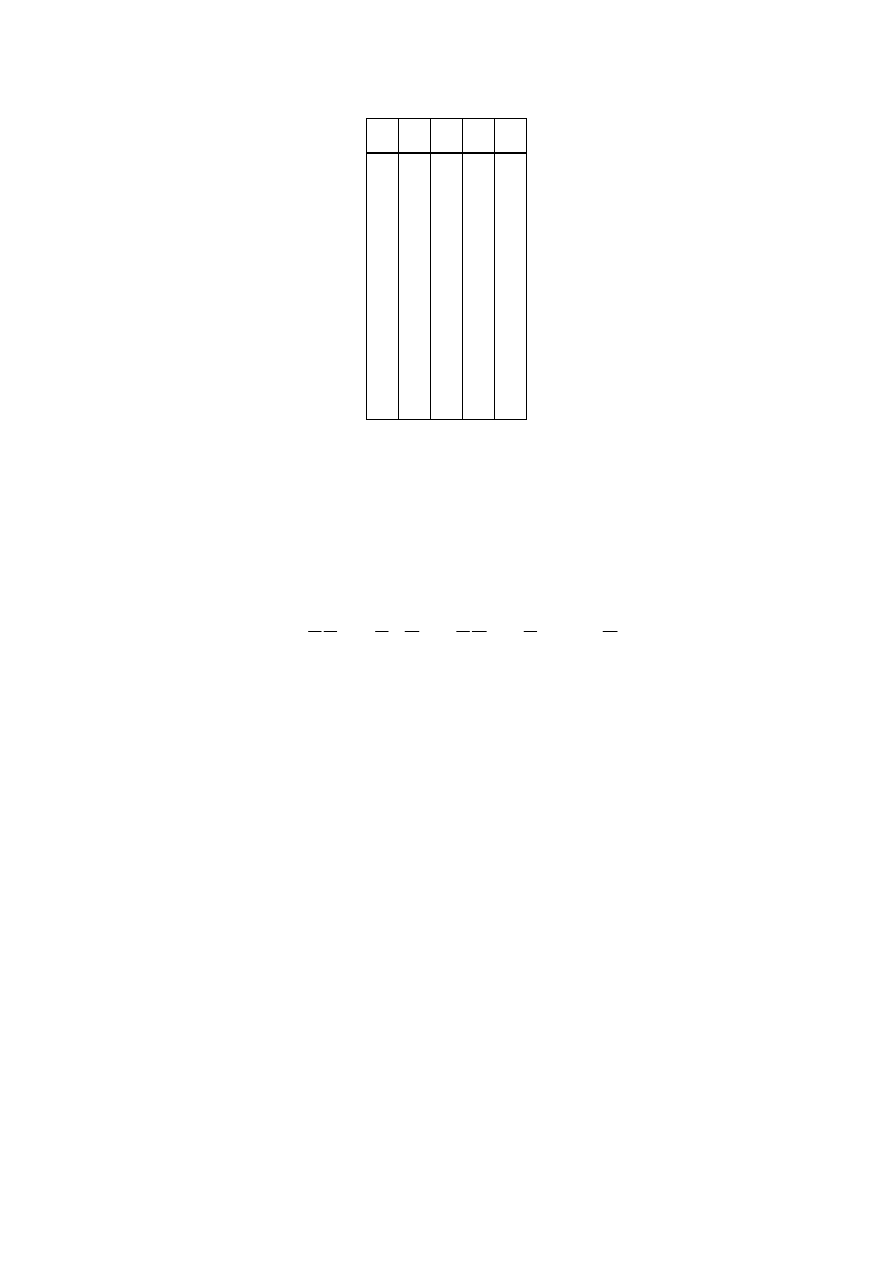
мов. Такой случай представлен в таблице 4.2. В ней единицы расположены в
строках 2 и 5, следовательно,
.
5
2
C
B
A
C
B
A
m
m
f
+
=
+
=
92
Таблица 4.2
№ A B C f
0 0 0 0 0
1 0 0 1 0
2 0 1 0 1
3 0 1 1 0
4 1 0 0 0
5 1 0 1 1
6 1 1 0 0
7 1 1 1 0
Если функция n аргументов представлена в виде дизъюнкции минтермов,
то говорят, что она записана в совершенной дизъюнктивной нормальной форме,
сокращённо СДНФ.
Пусть дана функция трёх аргументов, принимающая единичное значение
на наборах 001, 010, 100, 101 и 110. Каждому набору соответствует минтерм.
СДНФ имеет вид:
.
C
AB
C
B
A
C
B
A
C
B
A
C
B
A
f
+
+
+
+
=
Запишем эту функцию через обозначения минтермов:
.
6
5
4
2
1
m
m
m
m
m
f
+
+
+
+
=
Букву m можно удалить, оставив только номера наборов, на которых
функция равна единице:
f = (1, 2, 4, 5, 6).
Это наиболее компактное представление СДНФ. Им будем пользоваться
и в дальнейшем.
Всякая булева функция заданного числа аргументов представима в СДНФ
единственным образом. По этой причине СДНФ называют иногда стандарт-
ной формой [23].
В колонке f таблицы истинности n переменных может быть записано лю-
бое
n
2 -разрядное двоичное число, каждому из которых соответствует некото-
рая булева функция. Следовательно, всего существует
n
2
2
различных булевых
функций n переменных.

93
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Запишите двоичные наборы, на которых минтермы прини-
мают единичное значение:
1)
;
E
D
C
B
A
3)
;
D
C
B
A
5)
;
U
T
S
R
Q
P
2)
;
D
C
B
4)
;
Z
Y
VX
6)
.
2
1
X
X
2.
Укажите номера выражений, являющихся минтермами.
1)
;
C
AB
3)
;
PQRP
5)
;
C
ABA
7)
;
M
AC
2)
;
C
B
A
+
+
4)
;
B
K
AK
6)
;
D
BC
8)
.
C
B
AB
3.
Найдите десятичные индексы минтермов:
1)
;
D
C
B
A
2) Q; 3)
;
D
C
4) A; 5)
;
D
C
B
6) .
P
4.
Сколько существует минтермов шести аргументов, двоич-
ные индексы которых начинаются с нуля?
5.
Сколько существует минтермов семи аргументов, двоичные
индексы которых начинаются с двух нулей?
6.
Сколько существует минтермов семи аргументов, в каждом
из которых нет рядом стоящих инверсных переменных. Считать,
что буквы в записях минтермов идут в алфавитном порядке.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
4.8 Совершенная конъюнктивная нормальная форма
СДНФ функции, представленной в таблице 4.1, имеет вид:
f = (1, 2, 3, 4, 5).
Запишем СДНФ её инверсии. Для этого необходимо включить в инвер-
сию
f
все те и только те минтермы, которые не входят в заданную функцию:
f
= (0, 6, 7).
Запишем это выражение в аналитической форме:
.
f
ABC
ABC
ABC
=
+
+
Проинвертируем по теореме де Моргана (4.26) обе части выражения, ле-
вую и правую относительно знака равенства:
.)
)(
)(
(
C
B
A
C
B
A
C
B
A
f
+
+
+
+
+
+
=
Получили запись функции в виде конъюнкции дизъюнкций, где в каждую
дизъюнкцию входят все переменные (прямые в сочетании с инверсными), ука-
занные в таблице. Такие дизъюнкции называют максимальными термами или,

94
коротко, макстéрмами [4; 48], а функция, представленная в виде конъюнкции
макстермов, получила название совершенной конъюнктивной нормальной фор-
мой (СКНФ). Макстермы, как и минтермы, имеют и своё определение: макс-
термом n переменных называется такая их дизъюнкция, в которую каждая пе-
ременная входит один раз в прямой или инверсной форме [48, с. 49].
Макстермы условимся обозначать буквой M с десятичными индексами,
определяемыми по аналогии с индексами минтермов, т. е. записываем в заранее
заданном порядке буквы (как правило, алфавитном) и ставим в соответствие
инверсным буквам нуль, а неинверсным – единицу. Десятичный эквивалент по-
лучившегося двоичного числа есть искомый индекс макстерма. Например: дво-
ичный индекс макстерма
E
D
C
B
A
+
+
+
+
имеет вид 11010 согласно записи:
0
1
0
1
1
Е
D
C
B
A
В десятичной системе это число 26. Следовательно:
.
26
E
D
C
B
A
M
+
+
+
+
=
Минтерм есть инверсия макстерма, и макстерм – это инверсия минтерма,
при этом индексы их связаны между собой следующим образом:
2
1
2
1
;
,
− −
− −
=
=
n
n
i
i
i
i
m
M
M
m
(4.27)
где i = 0, 1, 2, …, n – 1.
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 4.4
· · · · · · · · · · · · · · · · · · · · · · ·
Найти индекс макстерма, если
.
11
CD
B
A
m =
Воспользуемся формулами (4.27):
11
16 11 1
4
4
;
.
− −
=
=
= + + +
m
M
M
M
A
B
C
D
Таким образом, минтерм
11
m – это инверсия макстерма
4
M .
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 4.5
· · · · · · · · · · · · · · · · · · · · · · ·
Представить в СКНФ булеву функцию трёх переменных A, B, C, задан-
ную дизъюнкцией минтермов
3
4
5
,
,
m m m , т. е.
f (A, B, C) = (3, 4, 5).

95
В эту функцию входит три минтерма, следовательно, СДНФ инверсии со-
стоит из пяти минтермов трёх переменных:
f
= (0, 1, 2, 6, 7) =
.
ABC
C
AB
C
B
A
C
B
A
C
B
A
+
+
+
+
Инвертируем инверсию СДНФ:
( , , ) (
)(
)(
)(
)(
)
=
+ +
+ +
+ +
+ +
+ +
=
f A B C
A
B
C A
B
C A
B
C A
B
C A
B
C
7
6
5
1
0
.
= M M M M M
Таким образом, выражение искомой СКНФ имеет вид:
.
7
6
5
1
0
M
M
M
M
M
f =
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
· · · · · · · · · · · · · · · · · · · · · · ·
Пример 4.6
· · · · · · · · · · · · · · · · · · · · · · ·
Перечислить в порядке возрастания десятичные индексы макстермов
функции
,
f
если
f (A, B, C, D) = (0, 1, 4, 7, 12, 14).
(4.28)
Записываем аналитическое выражение формулы (4.28):
.
D
ABC
D
C
AB
BCD
A
D
C
B
A
D
C
B
A
D
C
B
A
f
+
+
+
+
+
=
Инвертируем его по теореме де Моргана, так как требуется найти макс-
термы инверсии заданной функции:
(
)
(
)(
)
&
=
+ + +
+ + +
+ + +
f
A
B C
D
A
B C
D
A
B
C
D
(
)(
)(
)
15
14
11
8
3
1
&
.
+ + +
+ + +
+ + +
=
A
B
C
D
A
B
C
D
A
B
C
D
M M M M M M
Ответ: индексы макстермов идут в последовательности: 1, 3, 8, 11, 14,
15.
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
4.9 О формах высших порядков
Кроме ДНФ и КНФ существуют более сложные выражения, содержащие
различного вида скобки: круглые, квадратные, фигурные и др. Обычно класси-
фикация сложных выражений осуществляется на основе понятия порядка фор-
мулы, представляющей некоторую булеву функцию.
Булевы формулы, в которых нет знаков дизъюнкции и нет знаков конъ-
юнкции, имеют нулевой порядок:
f = 0, f = 1, f = A, f = .
B