ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16640
Скачиваний: 202
211
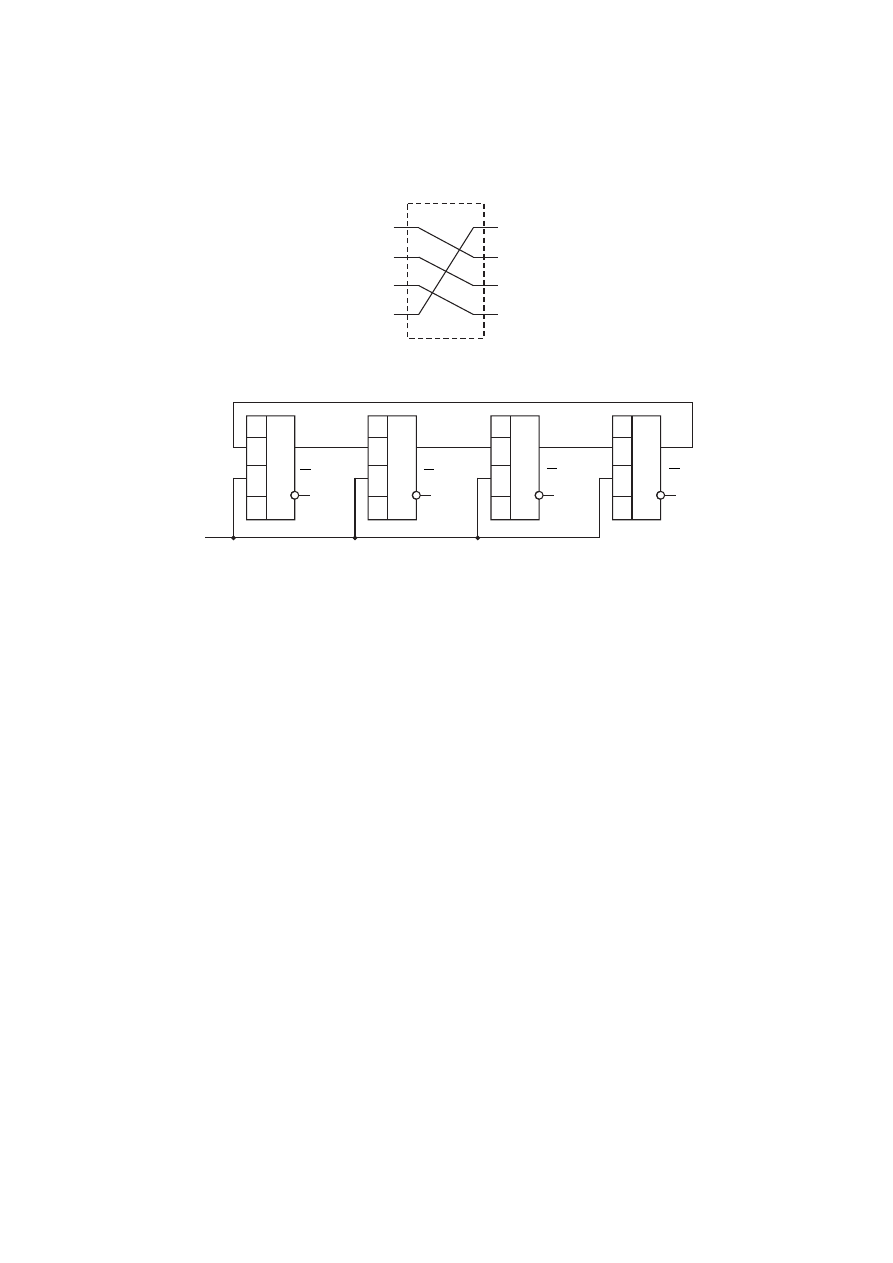
чится сдвиговый регистр (рис. 10.14). Хранящееся в нём число через комбина-
ционную схему, изображённую на рисунке 10.13, под действием синхроим-
пульса переписывается в этот же регистр.
Рис. 10.13
Рис. 10.14
В сущности, всякий многотактный автомат представляет собой сочетание
запоминающих регистров и комбинационных преобразователей, а работа авто-
мата сводится к переписи чисел из регистра в регистр через комбинационные
схемы. Даже при переписи чисел из регистра в регистр без каких-либо их пре-
образований имеется комбинационная схема.
Таким образом, работа практически любого цифрового устройства, со-
держащего триггерные регистры, сводится к операциям переписи чисел из ре-
гистра в регистр через комбинационные преобразователи. Кроме того, необхо-
димо отметить, что числа из регистра в регистр могут переписываться в момент
как положительных фронтов, так и отрицательных. Но в данной книге основное
внимание уделено переписи по отрицательным фронтам, так как именно этот
вариант переписи полностью согласуется с принятой в п. 7.1 интерпретацией
булевых формул и образует основу теории, обеспечивающей высокую эффек-
тивность её применения как в задачах синтеза комбинационных схем, так
и в задачах синхронных многотактных автоматов с памятью.
D
1
A
1
D
2
A
2
D
3
A
3
D
4
A
4
S
D
C
R
TT A
1
C
1
A
3
A
2
A
4
A
S
D
C
R
TT A
2
S
D
C
R
TT A
3
S
D
C
R
TT A
4

212
Заключение
В последние десятилетия выпущено много учебников и учебных пособий
по различным разделам дискретной математики. Примерами могут служить из-
дания [1; 2; 8; 14; 32; 33; 35; 38; 40; 51; 55; 57]. В основном подобные книги
рассчитаны на студентов очного обучения: во многих из них содержатся
упражнения, но нет ответов, т. е. самоконтроль исключён [14; 32; 33; 35; 40].
Кроме того, в подавляющем большинстве случаев их авторы ориентируются
главным образом на студентов как будущих профессиональных математиков,
вследствие чего если и уделяют внимание прикладным вопросам, то лишь
вскользь, эпизодически. Очевидно, что студентам системы дистанционного об-
разования, изучающим специальности с прикладным уклоном, необходимы
книги, в которых прикладные вопросы рассматриваются в гораздо большем
объёме и предусмотрена возможность самоконтроля при выполнении упражне-
ний. Эти два требования составили основу при разработке данного пособия.
Знания, полученные студентами при надлежащем усвоении материала,
изложенного в пособии, помогут им при изучении специальных дисциплин, где
в той или иной степени просматриваются дискретные структуры. Например,
комбинаторика необходима при изучении таких дисциплин, как теория вероят-
ностей, логико-лингвистические системы, информационные технологии и мно-
гие другие. При изучении программирования логических интегральных схем,
цифровой обработки сигналов, основ компьютерного проектирования и др.
находит применение алгебра логики. И вообще следует отметить, что разделы
дискретной математики, рассмотренные в пособии, так или иначе встречаются
в большинстве учебных предметов, относящихся к цифровой технике и учеб-
ным дисциплинам радиотехнического уклона.

213
Литература
1.
Акимов О. Е. Дискретная математика: логика, группы, графы /
О. Е. Акимов. – М. : Лаборатория Базовых Знаний, 2003. – 376 с.
2.
Березина Л. Ю. Графы и их применение : пособие для учителей /
Л. Ю. Березина. – М. : Просвещение, 1979. – 143 с.
3.
Борунова С. Н. Орфографический словарь русского языка: Произно-
шение, ударение, грамматические формы / С. Н. Борунова,
В. Л. Воронцова, Н. А. Еськова. – М. : Рус. яз., 1989. – 688 с.
4.
Бохманн Д. Двоичные динамические системы / Д. Бохманн,
Х. Постхоф ; пер. с нем. – М. : Энергоатомиздат, 1986. – 401 с.
5.
Бурова И. Н. Парадоксы теории множеств и диалектика /
И. Н. Бурова. – М. : Наука, 1976. – 176 с.
6.
Вавилов Е. Н. Синтез схем электронных цифровых машин /
Е. Н. Вавилов, Г. П. Портной. – М. : Сов. радио, 1963. – 440 с.
7.
Виленкин Н. Я. Комбинаторика / Н. Я. Виленкин, А. Н. Виленкин,
П. А. Виленкин. – М. : ФИМА, МЦНМО, 2006. – 400 с.
8.
Гаврилов Г. П. Сборник задач по дискретной математике / Г. П. Гав-
рилов, А. А. Сапоженко. – М. : Наука, 1977. – 368 с.
9.
Гетманова А. Д. Логика: Словарь и задачник / А. Д. Гетманова. – М. :
Гуманит. изд. центр «ВЛАДОС», 1998. – 336 с.
10.
Гжегорчик А. Популярная логика / А. Гжегорчик. – М. : Наука, 1972. –
111 с.
11.
Гиндикин С. Г. Алгебра логики в задачах / С. Г. Гиндикин. – М. :
Наука, 1972. – 288 с.
12.
Глушков В. М. Синтез цифровых автоматов / В. М. Глушков. – М. :
Физматгиз, 1962. – 476 с.
13.
Голышев
Л. К.
Электронные
вычислительные
машины
/
Л. К. Голышев. – Киев : Изд-во тех. лит. УССР, 1963. – 426 с.
14.
Горбатов В. А. Дискретная математика : учеб. для студентов втузов /
В. А. Горбатов, А. В. Горбатов, М. В. Горбатова. – М. : ООО «Изда-
тельство АСТ» ; ООО «Издательство Астрель», 2003. – 447 с.
15.
Горелик А. Л. Некоторые вопросы построения систем распознавания /
А. Л. Горелик, В. А. Скрипкин. – М. : Сов. радио, 1974. – 224 с.

214
16.
Грес П. В. Математика для гуманитариев / П. В. Грес. – М. : Универ-
ситетская книга, Логос, 2007. – 160 с.
17.
Ежов И. И. Элементы комбинаторики / И. И. Ежов, А. В. Скороход,
М. И. Ядренко. – М. : Гл. ред. физ.-мат. лит. изд-ва «Наука», 1977. –
80 с.
18.
Ершов Ю. Л. Математическая логика / Ю. Л. Ершов, Е. А. Палютин. –
М. : Наука, 1979. – 320 с.
19.
Ивин А. А. Логика / А. А. Ивин. – М. : Гардарики, 2001. – 224 с.
20.
Калбертсон Дж. Т. Математика и логика цифровых устройств /
Дж. Т. Калбертсон ; пер. с англ. – М. : Просвещение, 1965. – 267 с.
21.
Кибернетика и логика / отв. ред. Б. В. Бирюков, А. Г. Спиркин. – М. :
Наука, 1978. – 333 с.
22.
Клини С. К. Математическая логика / С. К. Клини ; пер. с англ. – М. :
Изд-во ЛКИ, 2008. – 480 с.
23.
Колдуэлл С. Логический синтез релейных устройств / С. Колдуэлл ;
пер. с англ. – М. : Изд-во иностр. лит., 1962. – 737 с.
24.
Колмогоров А. Н. Математическая логика. Дополнительные главы /
А. Н. Колмогоров, А. Г. Драгалин. – М. : Изд-во Моск. ун-та, 1984. –
119 с.
25.
Кондаков Н. И. Логический словарь-справочник / Н. И. Кондаков. –
М. : Наука, 1975. – 720 с.
26.
Корченко А. Г. Построение систем защиты информации на нечётких
множествах. Теория и практические решения / А. Г. Корченко. – Ки-
ев : МК-Пресс, 2006. – 320 с.
27.
Криницкий Н. А. Автоматизированные информационные системы /
Н. А. Криницкий, Г. А. Миронов, Г. Д. Фролов. – М. : Наука, 1982. –
384 с.
28.
Кузин Л. Т. Основы кибернетики : в 2 т. Т. 2. Основы кибернетиче-
ских моделей / Л. Т. Кузин. – М. : Энергия, 1979. – 584 с.
29.
Лавров И. А. Задачи по теории множеств, математической логике и
теории алгоритмов / И. А. Лавров, Л. Л. Максимова. – М. : Физматлит,
2002. – 256 с.
30.
Мендельсон Э. Введение в математическую логику / Э. Мендельсон ;
Пер. с англ. – М. : Наука, 1971. – 320 с.

215
31.
Мелихов А. Н. Ситуационные советующие системы с нечёткой логи-
кой / А. Н. Мелихов, Л. С. Бернштейн, С. Я. Коровин. – М. : Наука,
1990. – 272 с.
32.
Москинова Г. И. Дискретная математика. Математика для менеджера
в примерах и упражнениях / Г. И. Москинова. – М. : Логос, 2003. –
240 с.
33.
Нефедов В. Н. Курс дискретной математики / В. Н. Нефедов,
В. А. Осипова. – М. : Изд-во МАИ, 1992. – 264 с.
34.
Нешков К. И. Множества. Отношения. Числа. Величины /
К. И. Нешков, А. М. Пышкало, В. Н. Рудницкая. – М. : Просвещение,
1978. – 63 с.
35.
Новиков Ф. А. Дискретная математика для программистов. – СПб. :
Питер, 2003. – 304 с.
36.
Ожегов С. И. Толковый словарь русского языка / С. И. Ожегов,
Н. Ю. Шведова. – М. : АЗЪ, 1995, – 928 с.
37.
Очков В. Ф. Физико-математические этюды с Mathcad и Интернет /
В. Ф. Очков, Е. П. Богомолова, Д. А. Иванов. – СПб. : Лань, 2016. –
388 с.
38.
Палий И. А. Дискретная математика : курс лекций / И. А. Палий. –
М. : Эксмо, 2008. – 352 с.
39.
Папернов А. А. Логические основы цифровых машин и программиро-
вания / А. А. Папернов. – М. : Наука, 1968. – 591 с.
40.
Плотников А. Д. Дискретная математика : учеб пособие /
А. Д. Плотников. – М. : Новое знание, 2005. – 288 с.
41.
Политехнический словарь / гл. ред. И. И. Артоболевский. – М. : Со-
ветская энциклопедия, 1977. – 608 с.
42.
Савин А. П. Энциклопедический словарь юного математика /
А. П. Савин. – М. : Педагогика, 1989. – 352 с.
43.
Словарь иностранных слов / под ред. И. В. Лехина и др. – М. : Сов.
Энциклопедия, 1964. – 784 с.
44.
Советский энциклопедический словарь. – М. : Сов. Энциклопедия,
1985. – 1600 с.
45.
Столл Р. Р. Множества. Логика. Аксиоматические теории / Р. Р. Стол ;
пер с англ. – М. : Просвещение, 1968. – 231 с.
46.
Тараканов В. Е. Комбинаторные задачи и (0,1)-матрицы / В. Е. Тара-
канов. – М. : Наука, 1985. – 192 с.