ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 16644
Скачиваний: 202

206
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
Упражнения
1.
Автомат содержит четыре триггера типа JK. Триггеры обо-
значены буквами A, B, C, D. Работает автомат следующим образом.
Если A = 0, B = 0, то под действием синхроимпульсов число в реги-
стре, состоящем из триггеров C и D, меняется в последовательности
1, 2, 0, 3. Если A = 0, B = 1, то последовательность другая. Она име-
ет вид 2, 3, 1, 0. При A = 1, B = 0 реализуется последовательность 0,
1, 2, 3. Если принять A = 1, B = 1, то состояния регистра меняются в
последовательности 1, 3, 2, 0. Постройте схему автомата и опреде-
лите:
1) сколько единиц в колонке J
C
таблицы переходов?
2) сколько нулей в колонке J
D
таблицы переходов?
3) сколько существует наборов, на которых функция K
D
не
определена?
4) сколько букв в минимальной ДНФ функции J
C
? K
C
? J
D
? K
D
?
2.
Автомат, содержащий четыре триггера, обозначенные бук-
вами A, B, C, D, реализует замкнутую последовательность: 0, 1,
2, …, 14, 15. Постройте схему автомата и определите:
1) сколько единиц в колонке J
D
таблицы переходов?
2) сколько нулей в колонке K
D
таблицы переходов?
3) сколько состояний в колонке J
B
отмечены как неопреде-
лённые?
4) сколько букв в минимальной ДНФ функции J
A
? J
B
? J
C
? J
D
?
· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
10.6 Триггер типа D
На рисунке 10.10 изображена схема ещё одного универсального триггера,
известного в литературе под названием триггера типа D. Этот триггер имеет
синхровход и, подобно T-триггеру, один вход информационный. Если сравнить
его с JK-триггером, то нетрудно заметить, что схемы их мало отличаются одна
от другой: если вход K на рисунке 10.7 подключить к выходу инвертора, а вход
инвертора соединить со входом J, переименовав его на D, то получится D-
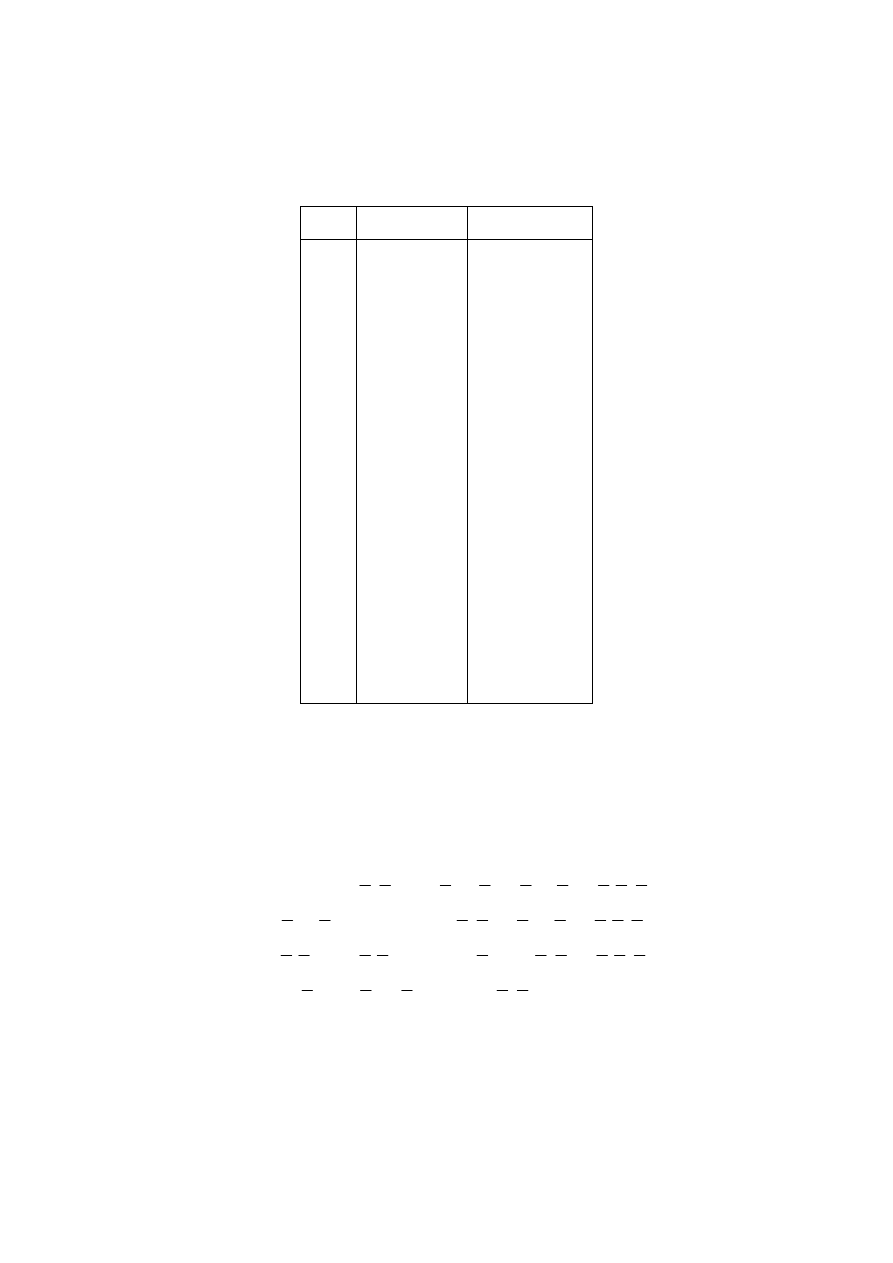
триггер. Условное обозначение D-триггера приведено на рисунке 10.11.
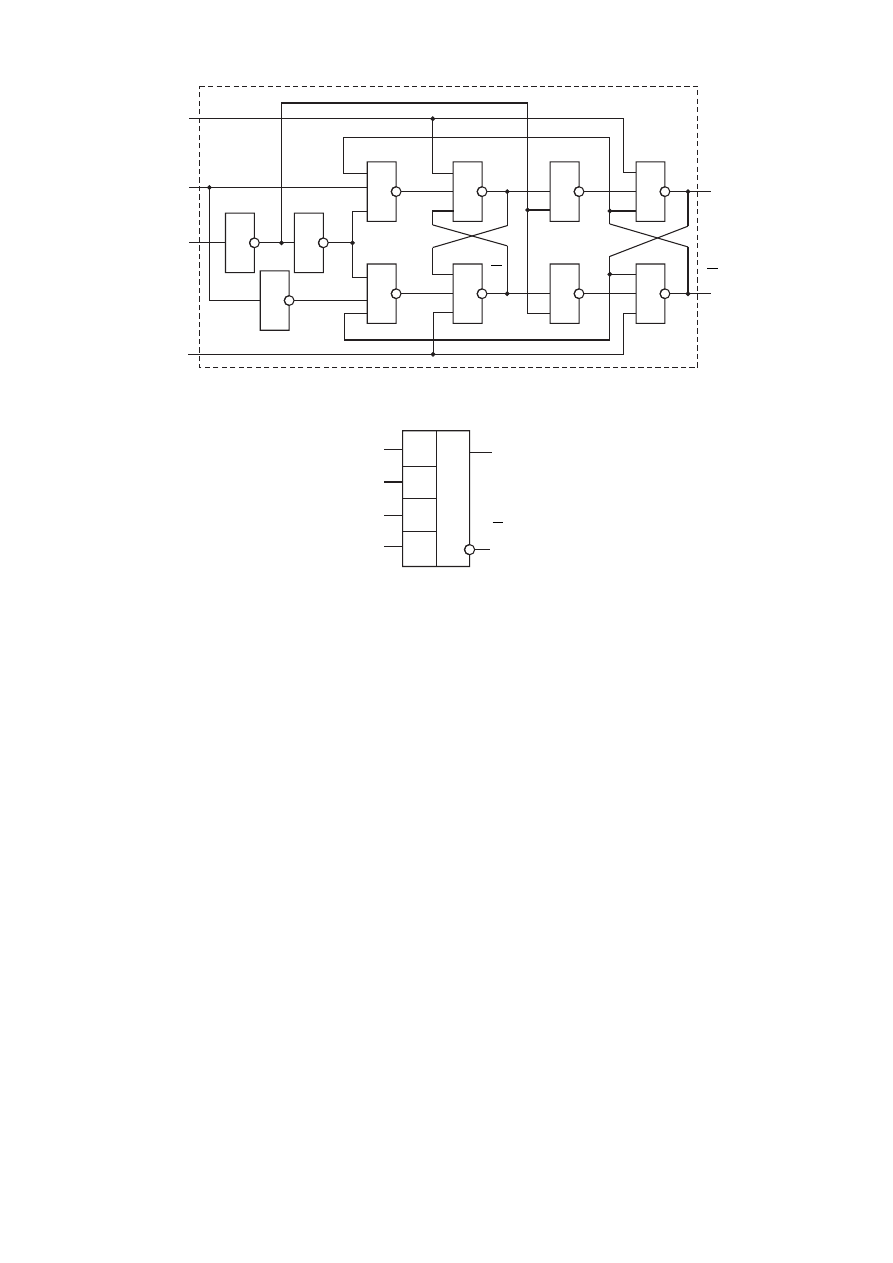
207
Рис. 10.10
Рис. 10.11
Логика работы D-триггера проста:
1)
если на вход D подать высокий уровень напряжения, то синхроим-
пульс переведёт триггер в единичное состояние;
2)
если на вход D подать низкий уровень, то синхроимпульс переведёт
триггер в нулевое состояние.
Иными словами: синхроимпульс переводит триггер в то состояние, какое
подано на его информационный вход D. Если на входе D низкий уровень, то
синхроимпульс переведёт триггер в нулевое стояние. Если на входе D высокий
уровень, то синхроимпульсом триггер переведётся в состояние единицы.
Рассмотрим пример, иллюстрирующий построение автомата на D-
триггерах табличным методом. Пусть автомат меняет свои состояния в замкну-
той последовательности вида:
1, 10, 11, 0, 14, 3, 2, 8, 7, 9, 13, 4, 5, 6, 15, 12.
Всего 16 состояний, следовательно, потребуется четыре триггера. Обо-
значим их буквами A
1
, A
2
, A
3
, A
4
.
Строим таблицу в соответствии с логикой ра-
боты D-триггера (табл. 10.4). Пусть начальным является состояние 0001, ука-
занное в левой части таблицы 10.4. Если на синхронизирующий вход поступит
импульс, то автомат должен перейти в состояние 1010, записанное во второй
S
Q
&
3
φ
3
&
P
&
5
φ
5
&
Q
&
4
φ
4
&
&
6
φ
6
&
P
1
1
φ
1
1
2
φ
2
D
C
R
1
S
Q
C
TT
D
R
Q
208
строке левой части таблицы 10.4. Чтобы переход состоялся, число 1010 запи-
шем справа от начального состояния 0001.
Таблица 10.4
Дес. A
1
A
2
A
3
A
4
D
1
D
2
D
3
D
4
1
10
11
0
14
3
2
8
7
9
13
4
5
6
15
12
0 0 0 1
1 0 1 0
1 0 1 1
0 0 0 0
1 1 1 0
0 0 1 1
0 0 1 0
1 0 0 0
0 1 1 1
1 0 0 1
1 1 0 1
0 1 0 0
0 1 0 1
0 1 1 0
1 1 1 1
1 1 0 0
1 0 1 0
1 0 1 1
0 0 0 0
1 1 1 0
0 0 1 1
0 0 1 0
1 0 0 0
0 1 1 1
1 0 0 1
1 1 0 1
0 1 0 0
0 1 0 1
0 1 1 0
1 1 1 1
1 1 0 0
0 0 0 1
Под действием следующего импульса автомат должен перейти в состоя-
ние 1011. Записываем его справа от кода 1010, находящегося во второй строке
левой половины таблицы 10.4.
Рассуждая аналогично, заполняем всю таблицу.
После минимизации получаем следующий список булевых функций:
1
2 3 4
2 3 4
2 3 4
1 3 4
1 2 3
2
1 2 4
1 2 4
1 2 3
1 2 3
1 3 4
3
1 2 4
1 3 4
2 3 4
1 2 4
1 2 3
4
2 4
1 4
1 2 3
1 2 3
;
;
;
.
D
A A A
A A A
A A A
A A A
A A A
D
A A A
A A A
A A A
A A A
A A A
D
A A A
A A A
A A A
A A A
A A A
D
A A
A A
A A A
A A A
=
+
+
+
+
=
+
+
+
+
=
+
+
+
+
=
+
+
+
Схема автомата, построенного на основе этой системы булевых функций,
приведена на рисунке 10.12. Схема изображена по упрощённому варианту: про-
вода, соединяющие входы комбинационной схемы и выходы триггеров, не
изображены, вместо них указаны только буквы, как адреса, показывающие, к
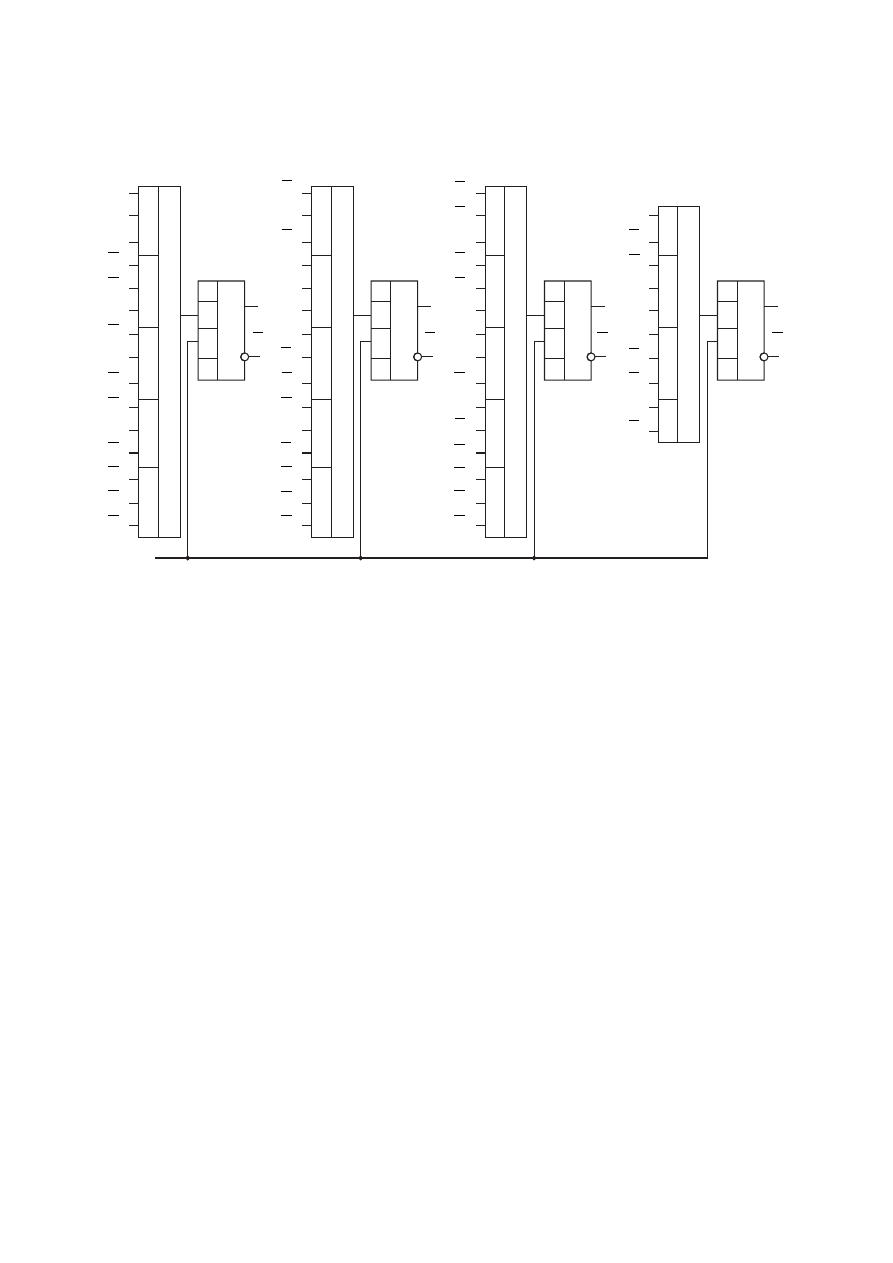
209
какому триггеру должен быть подключен тот или иной вход комбинационной
части автомата.
Рис. 10.12
10.7 Автомат с памятью – это сочетание запоминающих
элементов и комбинационных схем
На первый взгляд в многотактных устройствах главную роль играют за-
поминающие элементы, например триггеры, а что касается комбинационных
преобразователей, то в некоторых случаях можно обойтись и без них. На самом
же деле комбинационные схемы как преобразователи кодов есть во всех много-
тактных автоматах, за исключением отдельных (тривиальных) случаев. Проил-
люстрируем это на примере четырёхразрядного сдвигового регистра, основан-
ного на D-триггерах. Проведём его синтез табличным методом.
В левой части таблицы 10.5 перечислены все числа, которые могут быть
записаны в сдвиговый регистр при помощи установочных входов R и S.
В правой части каждому левому числу поставлено то же самое число, но сдви-
нутое вправо по замкнутому циклу. Например, в нулевой строке слева записано
число 0000. Так как единиц в этом числе нет, то после сдвига оно не изменится.
Соответственно в правой части нулевой строки записываем 0000. В первой
строке записано 0001. Если на вход сдвигового регистра подать импульс, то
вместо 0001 в нём должно оказаться число 1000. Именно это число записано
справа в первой строке таблицы 10.5.
S
&
D
C
R
TT A
1
&
&
&
&
1
C
A
2
A
3
A
4
A
4
A
3
A
3
S
&
D
C
R
TT
&
&
&
&
1
S
&
D
C
R
TT A
3
&
&
&
&
1
S
D
C
R
TT A
4
&
&
&
&
1
1
A
A
2
2
A
2
A
3
A
2
A
4
A
1
A
2
A
1
A
3
A
4
A
A
2
A
4
2
A
1
A
3
A
4
A
A
1
A
2
A
4
2
A
1
A
3
A
4
A
A
1
A
2
1
A
3
A
A
2
A
3
A
4
2
A
1
A
3
A
4
A
A
1
A
2
1
A
3
A
4
A
A
1
A
2
A
3
2
A
1
A
3
A
4
A
A
1
1
A
3
A
4
A
3
A
4
A

210
Таблица 10.5
Дес. A
1
A
2
A
3
A
4
D
1
D
2
D
3
D
4
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0 0 0 0
1 0 0 0
0 0 0 1
1 0 0 1
0 0 1 0
1 0 1 0
0 0 1 1
1 0 1 1
0 1 0 0
1 1 0 0
0 1 0 1
1 1 0 1
0 1 1 0
1 1 1 0
0 1 1 1
1 1 1 1
Аналогичным образом заполняем всю таблицу. Получилась таблица ис-
тинности для четырёх функций, D
1
, D
2
, D
3
, D
4
, описывающих работу комбина-
ционной схемы, преобразующей входное двоичное число в выходное, сдвину-
тое вправо на один разряд по замкнутому циклу. Входами преобразователя
служат выходы триггеров регистра, а выходы преобразователя выступают в ро-
ли уравнений входов тех же триггеров.
СДНФ и минимальные ДНФ функций D
1
, D
2
, D
3
, D
4
имеют вид:
D
1
= (1, 3, 5, 7, 9, 11, 13, 15) = A
4
;
D
2
= (8, 9, 10, 11, 12, 13, 14, 15) = A
1
;
D
3
= (4, 5, 6, 7, 12, 13, 14, 15) = A
2
;
D
4
= (2, 3, 6, 7, 10, 11, 14, 15) = A
3
.
Комбинационная схема, построенная на основе этих функций, приведена
на рисунке 10.13. В ней нет логических элементов, так как минимальные фор-
мы функций D
1
, D
2
, D
3
и D
4
являются предельно простыми, не содержащими
логических операций И, ИЛИ, НЕ (но если допустить ошибку при минимиза-
ции, то логические элементы могут появиться). Комбинационная схема состоит
только из отдельных проводов. Соединим этими проводами D-триггеры. Полу-