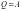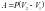ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.01.2019
Просмотров: 48262
Скачиваний: 391
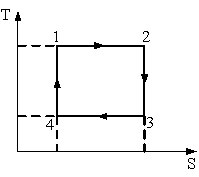
Изотермические процессы (т.е. T-const) 1-2 и 3-4. Изотермическое сжатие, отвод теплоты Q2 к холодильнику от рабочего тела, т.е Q<0, а значит энтропия S – уменьшается.
Ответ: 1
2.3.1-4
|
На рисунке изображен цикл Карно в координатах (T,S), где S-энтропия. Адиабатное сжатие происходит на этапе …
|
1: 4 – 1* 2: 1 – 2 3: 2 – 3 4: 3 – 4 |
Процессы 2-3 и 4-1 являются адиабатными. Адиабатное сжатие происходит на этапе возрастания температуры, т.е. на участке 4 – 1.
Ответ: 1
2.3.2-1
|
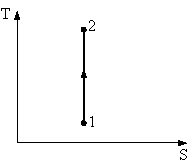
Процесс, изображенный на рисунке в координатах (T,S), где S-энтропия, является…
|
1: адиабатным сжатием* 2: изохорным нагреванием 3: изобарным расширением 4: изотермическим расширением |
Поскольку в процессе 1-2 не происходит изменения энтропии, то процесс является адиабатным. Т.к. температура Т увеличивается, то происходит процесс адиабатного сжатия.
Ответ: 1
2.3.2-2
|
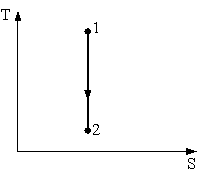
Процесс, изображенный на рисунке в координатах (T,S), где S-энтропия, является…
|
1: адиабатным расширением* 2: изохорным охлаждением 3: изобарным сжатием 4: изотермическим сжатием |
Поскольку в процессе 1-2 не происходит изменения энтропии, то процесс является адиабатным. Т.к. температура Т уменьшается, то происходит процесс адиабатного расширения.
4.4.1-1
|
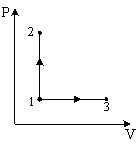
Молярные теплоемкости гелия в процессах 1-2 и 1-3 равны С1 и С2 соответственно.
|
1:
2:
3:
4:
|
При
изохорном процессе (V
– const),
на графике 1-2, молярная теплоемкость
равна
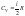 ,
при изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
,
при изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
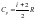 ,
где i–число
степеней свободы гелия равно 3, т.к.
одноатомный газ.
,
где i–число
степеней свободы гелия равно 3, т.к.
одноатомный газ.
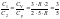
Ответ: 3
4.4.1-2
|
Молярные теплоемкости гелия в процессах 1-2 и 1-3 равны С1 и С2 соответственно.
|
1:
2:
3:
4:
|
При
изохорном процессе (V
– const),
на графике 1-2, молярная теплоемкость
равна
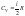 ,
при изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
,
при изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
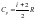 ,
где i–число
степеней свободы гелия равно 3, т.к.
одноатомный газ.
,
где i–число
степеней свободы гелия равно 3, т.к.
одноатомный газ.
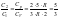
Ответ: 1
4.4.1-3
|
Молярные теплоемкости молекулярного водорода (при условии, что связь атомов в молекуле - жесткая) в процессах 1-2 и 1-3 равны С1 и С2 соответственно.
|
1:
2:
3:
4:
|
При
изохорном процессе (V
– const),
на графике 1-2, молярная теплоемкость
равна
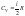 ,
при изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
,
при изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
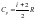 ,
где i–число
степеней свободы молекулярного водорода
с жёсткой связью равно 5, т.к. двухатомный
газ.
,
где i–число
степеней свободы молекулярного водорода
с жёсткой связью равно 5, т.к. двухатомный
газ.
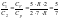
Ответ: 1
4.4.1-4
|
Молярные теплоемкости молекулярного водорода (при условии, что связь атомов в молекуле - жесткая) в процессах 1-2 и 1-3 равны С1 и С2 соответственно.
|
1:
2:
3:
4:
|
При
изохорном процессе (V
– const),
на графике 1-2, молярная теплоемкость
равна
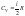 ,
при изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
,
при изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
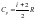 ,
где i–число
степеней свободы молекулярного водорода
с жёсткой связью равно 5, т.к. двухатомный
газ.
,
где i–число
степеней свободы молекулярного водорода
с жёсткой связью равно 5, т.к. двухатомный
газ.
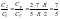
Ответ: 1
4.4.1-5
|
Молярные теплоемкости двухатомного газа (при условии, что связь атомов в молекуле - упругая) в процессах 1-2 и 1-3 равны С1 и С2 соответственно.
|
1:
2:
3:
4:
|
При
изохорном процессе (V
– const),
на графике 1-2, молярная теплоемкость
равна
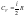 .
При изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
.
При изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
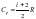 ,
где i
–
число степеней свободы двухатомного
газа (при условии, что связь атомов –
упругая) равно 7. Двухатомная нежесткая
молекула имеет одну колебательную, две
вращательные и три поступательные
степени свободы, а
,
где i
–
число степеней свободы двухатомного
газа (при условии, что связь атомов –
упругая) равно 7. Двухатомная нежесткая
молекула имеет одну колебательную, две
вращательные и три поступательные
степени свободы, а
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]() – число степеней свободы поступательного,
вращательного и колебательного движений
молекулы.
– число степеней свободы поступательного,
вращательного и колебательного движений
молекулы.
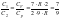 .
.
Ответ: 1
4.4.1-6
|
Молярные теплоемкости двухатомного газа (при условии, что связь атомов в молекуле - упругая) в процессах 1-2 и 1-3 равны С1 и С2 соответственно.
|
1:
2:
3:
4:
|
При
изохорном процессе (V
– const),
на графике 1-2, молярная теплоемкость
равна
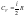 .
При изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
.
При изобарном процессе (P
– const),
на графике 1-3, молярная теплоемкость
равна
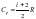 ,
где i
–
число степеней свободы двухатомного
газа (при условии, что связь атомов –
упругая) равно 7. Двухатомная нежесткая
молекула имеет одну колебательную, две
вращательные и три поступательные
степени свободы, а
,
где i
–
число степеней свободы двухатомного
газа (при условии, что связь атомов –
упругая) равно 7. Двухатомная нежесткая
молекула имеет одну колебательную, две
вращательные и три поступательные
степени свободы, а
![]() ,
где
,
где
![]() ,
,
![]() и
и
![]() – число степеней свободы поступательного,
вращательного и колебательного движений
молекулы.
– число степеней свободы поступательного,
вращательного и колебательного движений
молекулы.
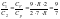 .
.
Ответ: 1
4.4.2-1
|
Состояние
идеального газа определяется значениями
параметров: T0,
p0,
V0,
где Т – термодинамическая температура,
p – давление, V – объем газа. Определенное
количество газа перевели из состояния
|
1: уменьшилась 2: не изменилась 3: увеличилась* |
Изменение
внутренней энергии идеального газа
вычисляется по формуле:
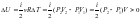 .
.
Ответ: 3
4.4.2-2
|
Состояние
идеального газа определяется значениями
параметров: T0,
p0,
V0,
где Т – термодинамическая температура,
p – давление, V – объем газа. Определенное
количество газа перевели из состояния
|
1: уменьшилась* 2: увеличилась 3: не изменилась |
Изменение
внутренняя энергия идеального газа
вычисляется по формуле:
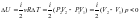 .
.
Ответ: 1
4.4.2-3
|
Состояние
идеального газа определяется значениями
параметров: T0,
p0,
V0,
где Т – термодинамическая температура,
p – давление, V – объем газа. Определенное
количество газа перевели из состояния
|
1: не изменилась* 2: увеличилась 3: уменьшилась |
Изменение
внутренней энергии идеального газа
вычисляется по формуле:
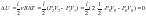 .
.
Ответ: 1
4.4.2-4
|
Состояние
идеального газа определяется значениями
параметров: T0,
p0,
V0,
где Т – термодинамическая температура,
p – давление, V – объем газа. Определенное
количество газа перевели из состояния
|
1: увеличилась* 2: уменьшилась 3: не изменилась |
Изменение
внутренней энергии идеального газа
вычисляется по формуле:
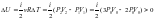 .
.
Ответ: 1
4.4.2-5
|
Состояние
идеального газа определяется значениями
параметров: T0,
p0,
V0,
где Т – термодинамическая температура,
p – давление, V – объем газа. Определенное
количество газа перевели из состояния
|
1: уменьшилась* 2: увеличилась 3: не изменилась |
Изменение
внутренней энергии идеального газа
вычисляется по формуле:
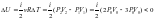 .
.
Ответ: 1
4.4.3-1
|
Среди приведённых формул к изотермическому процессу имеют отношение |
1.
2.
3.
4.
5.
|
 – адиабатный
процесс;
– адиабатный
процесс;
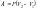 – изобарный процесс;
– изобарный процесс;
 – адиабатный процесс.
– адиабатный процесс.
Ответы: 1 и 5
4.4.4-1
|
Если
|
1:
2:
3:
4:
|
Адиабатное
расширение характеризуется: Q=0,
V2>V1,
T2<T1.
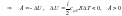 .
.
Ответ: 4
4.4.4-2
|
Если
|
1:
2:
3:
4:
|
Адиабатное
сжатие характеризуется: Q=0,
V2<V1,
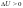 ,
,
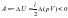 .
.
Ответ: 1
4.4.4-3
|
Если
|
1:
2:
3:
4:
|
Изохорное
охлаждение характеризуется: V=const,
A=0,
Q<0,
 .
.
Ответ: 1
4.4.4-4
|
Если
|
1:
2:
3:
4:
|
Изохорное
охлаждение характеризуется: V=const,
A=0,
Q<0,
 .
.
Ответ: 1
4.4.4-5
|
Если
|
1:
2:
3:
4:
|
A<0, Q<0; ΔU= A – Q; ΔU<0.
Внутренняя энергия уменьшается за счёт того, что над газом совершается работа и газ отдаёт тепло окружающей среде.
Ответ: 1
4.4.4-6
|
Если
|
1:
2:
3:
4:
|
A<0, Q<0; А = – Q; ΔU=0.
При совершении работы внешними силами газ отдаёт тепло окружающей среде.
Ответ: 1
4.4.4-7
|
Если
|
1: 2: 3: 4: |
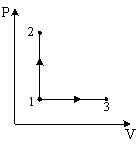
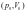 в состояние
в состояние
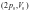 .
При этом его внутренняя энергия…
.
При этом его внутренняя энергия…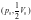 .
При этом его внутренняя энергия…
.
При этом его внутренняя энергия…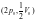 .
При этом его внутренняя энергия…
.
При этом его внутренняя энергия…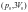 .
При этом его внутренняя энергия…
.
При этом его внутренняя энергия…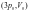 в
состояние
в
состояние
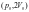 .
При этом его внутренняя энергия…
.
При этом его внутренняя энергия…