ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.01.2019
Просмотров: 48259
Скачиваний: 391
Ф1.1.8-2
|
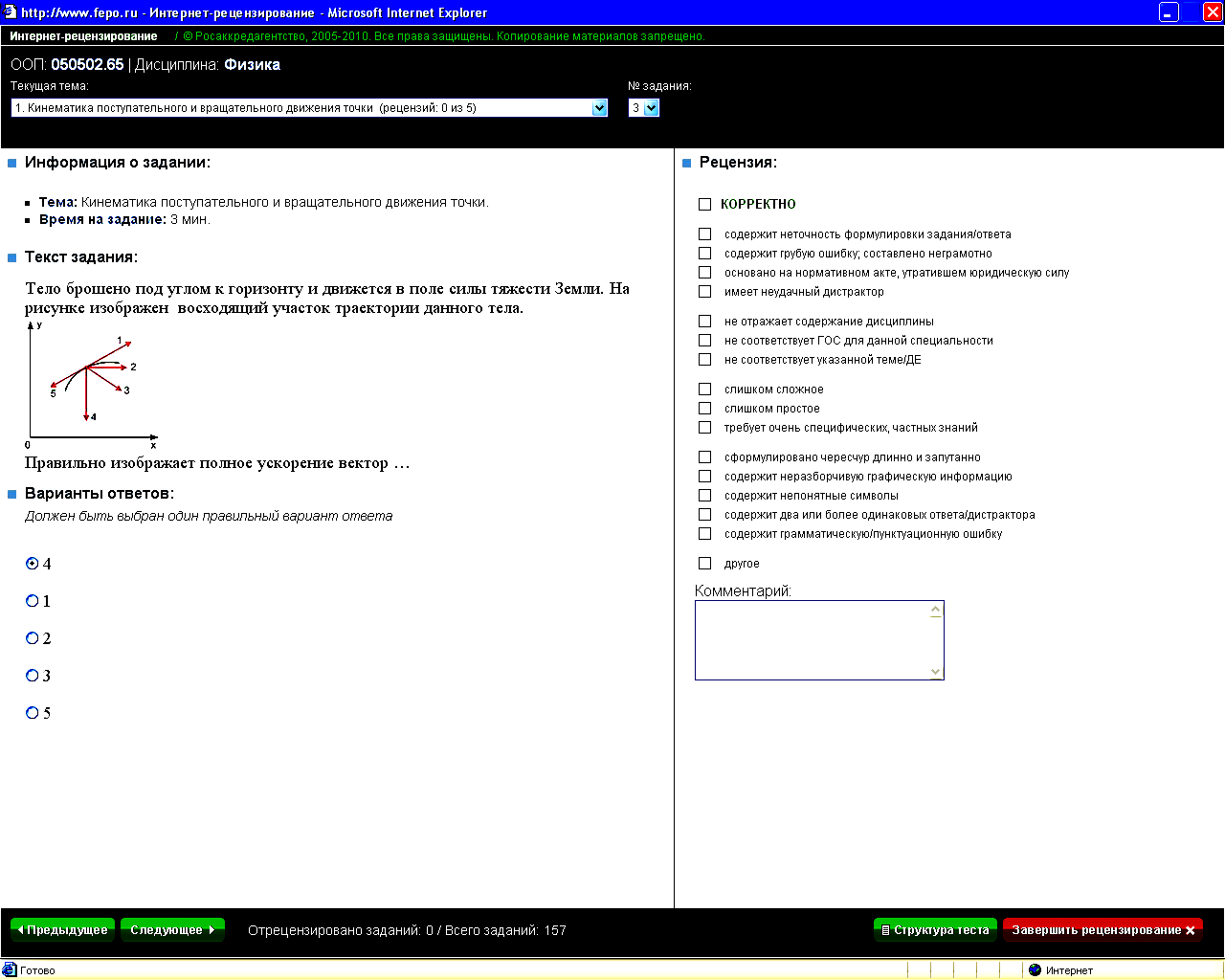
Тело брошено под углом к горизонту и движется в поле силы тяжести Земли. На рисунке изображён восходящий участок траектории данного тела.
Правильно изображает полное ускорение вектор … |
1. 4* 2. 1 3. 2 4. 3 5. 5 |
|
|
|
Ф1.1.9-1
|
Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1м с постоянным угловым ускорением ε=2с-2. Отношение нормального ускорения к тангенциальному через одну секунду равно … |
1. 3 2. 2* 3. 4 4. 8 5. 1 |
|
Ускорение
частицы при движении по окружности
|
|
Ф1.1.10-1
|
Камень бросили под углом к горизонту со скоростью VО. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.
Модуль
тангенциального ускорения
|
1. увеличивается 2. уменьшается* 3. не изменяется |
|
В
Тогда
для модуля скорости с учетом (1) имеем:
Используя полученное соотношение находим выражение для проекции тангенциального ускорения:
Величина
|
|
Ф1.1.10-2
|
Камень бросили под углом к горизонту со скоростью VО. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.
Тангенциальное
ускорение
|
1.
2.
3.
|
|
|
|
Ф1.1.10-3
|
Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.
Модуль полного ускорения камня … |
1. во всех точках одинаков 2. максимален в точках А и Е 3. максимален в точках B и D 4. максимален в точках C |
|
|
|
Ф1.1.10-4
|
Два тела брошены под одним и тем же углом к горизонту с начальными скоростями VО и 2VО. Если сопротивлением воздуха пренебречь, то соотношение дальностей полёта S2/S1 равно … |
1. 4* 2.
3. 2 4.
|
|
Дальность
полета тела, брошенного с поверхности
земли, определяется соотношением:
|
|
Ф1.1.11-1
|
Диск
вращается вокруг своей оси, изменяя
проекцию своей угловой скорости
Вектор угловой скорости направлен по оси Z в интервалы времени |
1. от t1 до t2 и от t3 до t4 2. от t1 до t2 и от t2 до t3 3. от t2 до t3 и от t3 до t4 4. от 0 до t1 и от t1 до t2* |
|
Когда вектор угловой скорости направлен по оси Z её проекция ωz > 0. Этому условию удовлетворяют на графике моменты времени от 0 до t1 и от t1 до t2. Ответ: 4 |
|
Ф1.1.11-2
|
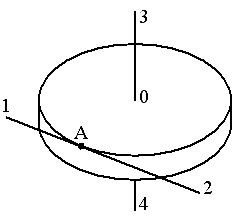
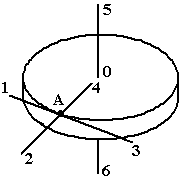
Диск радиуса R вращается вокруг вертикальной оси равноускоренно по часовой стрелке. Укажите направление вектора углового ускорения.
|
1: 4* 2: 3 3: 1 4: 2 |
|
Б |
|
Ф1.1.11-3
|
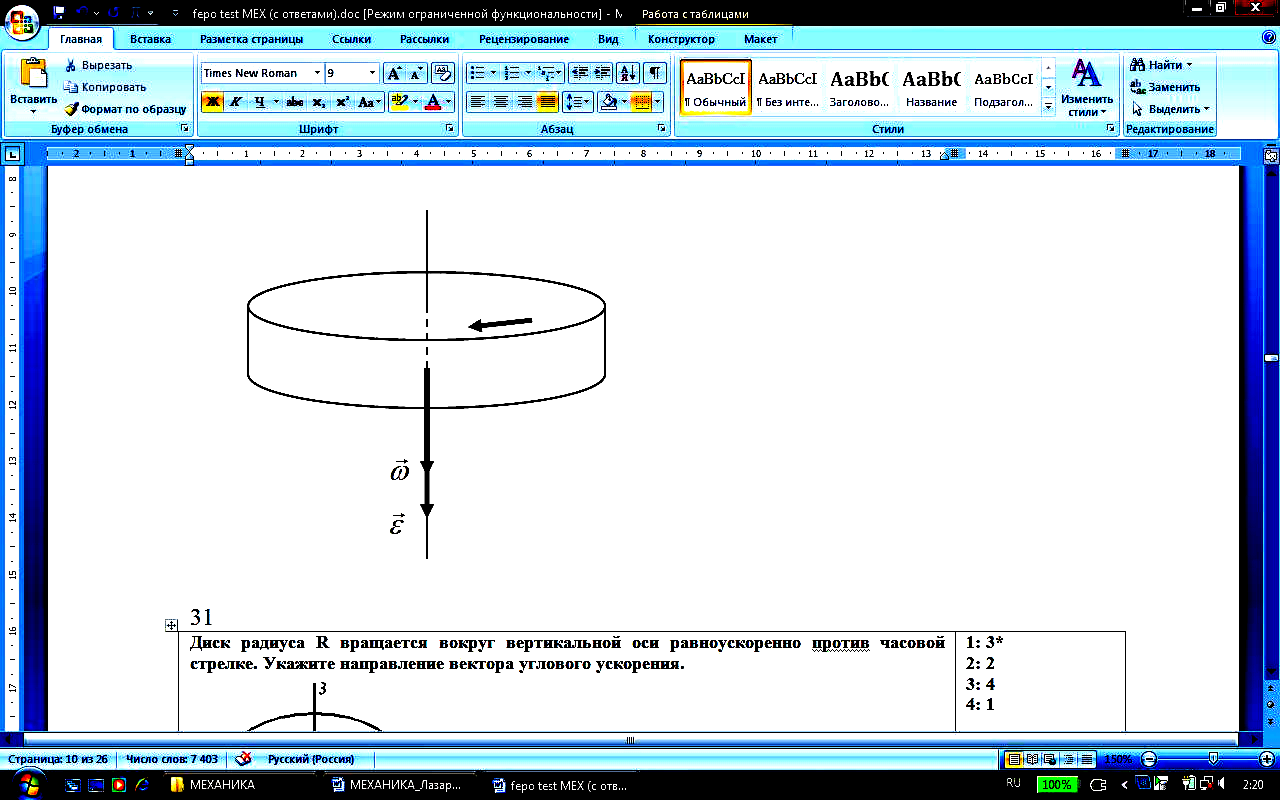
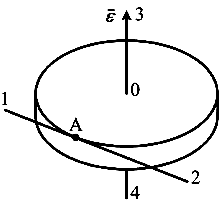
Диск радиуса R вращается вокруг вертикальной оси равноускоренно против часовой стрелке. Укажите направление вектора углового ускорения.
|
1: 3* 2: 2 3: 4 4: 1 |
|
Будем считать, что диск вращается против часовой стрелки, если смотреть на него сверху. Тогда его угловая скорость будет направлена вертикально вверх. При равноускоренном движении направление углового ускорения будет совпадать с направлением угловой скорости – в данном случае угловое ускорение будет направлено вертикально вверх или по направлению 3. Ответ: 1 |
|
Ф1.1.11-4
|
Диск радиуса R вращается вокруг вертикальной оси равнозамедленно по часовой стрелке. Укажите направление вектора углового ускорения.
|
1: 3* 2: 2 3: 4 4: 1 |
|
Будем считать, что диск вращается по часовой стрелке, если смотреть на него сверху. Тогда его угловая скорость будет направлена вертикально вниз. При равнозамедленном движении направление углового ускорения будет направлено противоположно направлению угловой скорости – в данном случае угловое ускорение будет направлено вертикально вверх или по направлению 3. Ответ: 1 |
|
Ф1.1.11-5
|
Диск радиуса R вращается вокруг вертикальной оси равнозамедленно против часовой стрелки. Укажите направление вектора углового ускорения.
|
1: 4* 2: 2 3: 3 4: 1 |
|
Будем считать, что диск вращается против часовой стрелки, если смотреть на него сверху. Тогда его угловая скорость будет направлена вертикально вверх. При равнозамедленном движении направление углового ускорения будет направлено противоположно направлению угловой скорости – в данном случае угловое ускорение будет направлено вертикально вниз или по направлению 4. Ответ: 1 |
|
Ф1.1.11-6
|
Диск
радиуса R вращается вокруг вертикальной
оси равноускоренно с заданным
направлением вектора углового ускорения
|
1: 2* 2: 1 3: 4 4: 3 |
|
П |
|
Ф1.1.11-7
|
Диск
радиуса R
вращается
вокруг вертикальной оси равноускоренно
с заданным направлением вектора
углового ускорения
|
1: 1* 2: 2 3: 3 4: 4 |
|
При
равноускоренном движении направление
угловой скорости
|
|
Ф1.1.11-8
|
Диск
радиуса R вращается вокруг вертикальной
оси равнозамедленно с заданным
направлением вектора углового ускорения
|
1: 1* 2: 2 3: 3 4: 4 |
|
При
равнозамедленном движении направление
угловой скорости
|
|
Ф1.1.11-9
|
Диск
радиуса R вращается вокруг вертикальной
оси равнозамедленно с заданным
направлением вектора углового ускорения
|
1: 2* 2: 1 3: 4 4: 3 |
|
При
равнозамедленном движении направление
угловой скорости
|
|
Ф1.1.12-1
|
Частица
движется вдоль окружности радиусом
1 м в соответствии с уравнением
|
1: 3 2: 1 3: 9* 4: 6 |
|
Обозначим
момент времени, соответствующий
остановки частицы, за t1.
В этот момент
|
|
Ф1.1.12-2
|
Частица
движется вдоль окружности радиусом
1 м в соответствии с уравнением
|
1: 0* 2: 4π 3: 16π2 4: 64π2 |
|
Нормальное
ускорение в момент времени t1
= 3
c
определяется соотношением
|
|
Ф1.1.12-3
|
Частица
движется вдоль окружности радиусом
1 м в соответствии с уравнением
|
1: 4π* 2: 2π 3: 0 4: 6π |
|
Тангенциальное
ускорение определяется соотношением
|
|
Ф1.1.12-4
|
Частица
движется вдоль окружности радиусом
1 м в соответствии с уравнением
|
1: 4π* 2: 2π 3: 0 4: 6π |
|
Величина
модуля углового ускорения
|
|
Ф1.1.12-5
|
Вращение
твердого тела происходит по закону
|
1: 51 рад/c2* 2: 68 рад/c2 3: 17 рад/c2 4: 102 рад/c2 |
|
|
|
Ф1.1.13-1
|
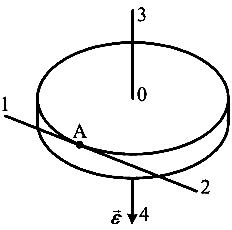
Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике.
За все время вращения тело сможет повернуться относительно начального положения на максимальный угол … |
1: 21 рад* 2: 4 рад 3: 5 рад 4: 9 рад |
1. Частица пересекает ось Х в точке С, двигаясь в направлении 1. Укажите направление вектора момента импульса этой частицы относительно начала координат.
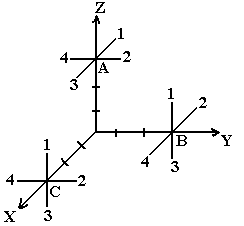
1) -Y
2) Y
3) Х
4) -X
5) -Z
6) Z
2. Сила приложена в точке С перпендикулярно оси Х. Укажите направление этой силы, если вектор ее момента относительно начала координат направлен вдоль оси –У.
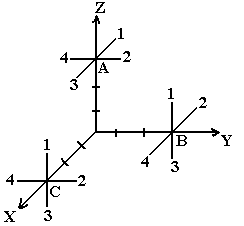
1) Z
2) Х
3) -Y
4) -X
5) Y
6) -Z
3. Момент инерции какого тела наибольший, относительно указанной оси? Массы и радиусы тел одинаковы.
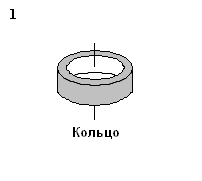
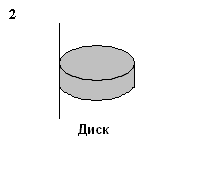
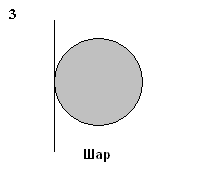
|
1) 2 |
2) 1 |
3) 3 |
4. При пуске электродвигателя якорь приобрел момент импульса 35 Дж·с. В течение какого времени на якорь действовал момент силы величиной 7 Н·м?
5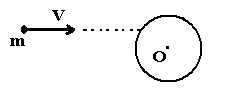 .
Маленький шарик
массой 10г, двигаясь со скоростью 10м/с,
ударяется в закрепленный на горизонтальной
оси цилиндр (рис.) массой 1кг и радиусом
R=10см.
Линия удара проходит на расстоянии
.
Маленький шарик
массой 10г, двигаясь со скоростью 10м/с,
ударяется в закрепленный на горизонтальной
оси цилиндр (рис.) массой 1кг и радиусом
R=10см.
Линия удара проходит на расстоянии
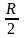 от оси цилиндра.
Укажите значение момента импульса
шарика до удара относительно т.О.
от оси цилиндра.
Укажите значение момента импульса
шарика до удара относительно т.О.
|
1) 0,1 кг·м2/с |
2) 0,5 кг·м2/с |
3) 500 кг·м2/с |
4) 0,005 кг·м2/с |
6. Потенциальная энергия частицы задается функцией. U=xyz. Чему равна работа по перемещению этой частицы из т. А (1,1,1) в т. В (2,2,2) (Данные приведены в системе СИ)?
7. На рисунке показаны тела одинаковой массы, вращающиеся вокруг вертикальной оси с одинаковой частотой. Чему равно отношение их кинетических энергий Т1/Т2?
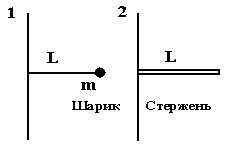
1) 1
2) 12
3) 1/3
4) 3
8. Обруч скатывается без проскальзывания с горки высотой 2,5 м. Какую скорость он будет иметь у основания горки? Трением пренебречь.
|
9. Частица пересекает ось Х в точке С, двигаясь в направлении 1. Импульс частиц равен 1 кг·м/с. Укажите вектор момента импульса относительно начала координат, соответствующий данному случаю. |
|
|
1) (0;0;3) |
2) (0;-3;0) |
3) (3;0;0) |
4) (0;0;-3) |
5) (-3;0;0) |
6) (0;3;0) |
10. Сила в 1 Н приложена в точке С перпендикулярно оси Х. Укажите направление этой силы, если вектор ее момента относительно начала координат имеет координаты (0,-3,0).
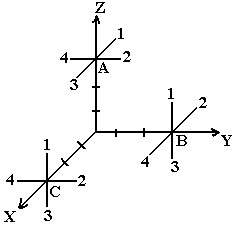
1) 3
2) 2
3) 4
4) 1
11. Укажите верное соотношение для моментов инерции тел относительно указанных осей. Массы и радиусы тел одинаковы.
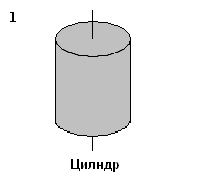
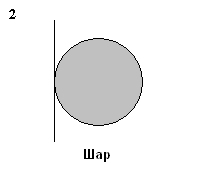
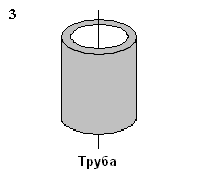
|
1)
|
2)
|
3)
|
4)
|
1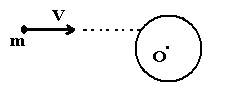 2.
Маленький шарик
массой 10г, двигаясь со скоростью 10м/с,
ударяется в закрепленный на горизонтальной
оси цилиндр (рис.) массой 1кг и радиусом
R=10см.
Линия удара проходит на расстоянии
2.
Маленький шарик
массой 10г, двигаясь со скоростью 10м/с,
ударяется в закрепленный на горизонтальной
оси цилиндр (рис.) массой 1кг и радиусом
R=10см.
Линия удара проходит на расстоянии
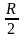 от оси цилиндра.
Какова угловая скорость цилиндра после
абсолютно неупругого удара?
от оси цилиндра.
Какова угловая скорость цилиндра после
абсолютно неупругого удара?
1) 1,0 с-1 2) 0,5 с-1 3) 2,0 с-1 4) 0,25 с-1
13. Потенциальная энергия частицы задается функцией. U=xyz. Определите компоненты вектора силы, действующей на частицу в т. А (1,2,3). Координаты т.А заданы в системе СИ. Введите компоненты вектора силы в скобках через запятую, например: (2,-3,1).
1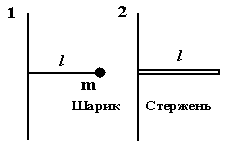 4.
На рисунке показаны
тела одинаковой массы m,
вращающиеся вокруг вертикальной оси с
одинаковой частотой. Момент импульса
первого тела 0,1Дж·с. Чему равна кинетическая
энергия второго тела, если m=1кг,
L=10см.?
4.
На рисунке показаны
тела одинаковой массы m,
вращающиеся вокруг вертикальной оси с
одинаковой частотой. Момент импульса
первого тела 0,1Дж·с. Чему равна кинетическая
энергия второго тела, если m=1кг,
L=10см.?
1) 0,25 Дж
2) 0,20 Дж
3) 0,17 Дж
4) 0,50 Дж
15. Шар и диск одинаковых масс и радиуса вкатываются без проскальзывания с одинаковыми скоростями на горку. Найдите отношение высот Н1/Н2, на которые смогут подняться эти тела. Трением пренебречь.
|
1)
|
2)
|
3) 1 |
4)
|
Правильные ответы
|
Задание № |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
Ответ |
1 |
1 |
1 |
5 |
4 |
-7 |
4 |
5 |
2 |
4 |
3 |
1 |
(-6,-3,-2) |
3 |
1 |
|
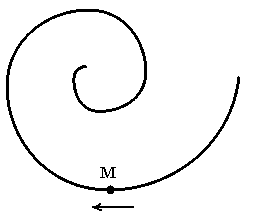
1. Точка М движется по спирали с постоянной по величине скоростью. При этом величина нормального ускорения 1)
не изменяется |
|
|
2.
Диск радиуса R
вращается вокруг вертикальной оси
равноускоренно по часовой стрелке.
Укажите направление вектора угловой
скорости
|
|
|||||
|
1) 2 |
2) 6 |
3) 3 |
4) 1 |
5) 4 |
6) 5 |
|
|
3.
Обруч катится
равномерно со скоростью
|
|
|||||||
|
1) 2 |
2) 5 |
3) 1 |
4) 3 |
5) 6 |
6) 8 |
7) 4 |
8) 7 |
|
4. Колесо радиусом 10 cм вращается вокруг неподвижной оси. Зависимость линейной скорости точек на ободе колеса от времени задается уравнением V=3t+t2 (см/с). Какая функция описывает зависимость угловой скорости от времени?
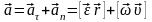 .
Модуль тангенциального ускорения
.
Модуль тангенциального ускорения
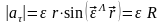 .
Нормальное ускорение
.
Нормальное ускорение
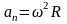 .
Поскольку частица движется с постоянным
угловым ускорением, то для угловой
скорости справедливо уравнение
.
Поскольку частица движется с постоянным
угловым ускорением, то для угловой
скорости справедливо уравнение
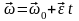 .
По условию в начальном состоянии
частица находилась в покое, поэтому
.
По условию в начальном состоянии
частица находилась в покое, поэтому
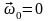 и
и
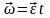 ,
,
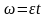 .
Для момента времени
.
Для момента времени 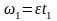 .
Тогда нормальное ускорение в момент
времени
.
Тогда нормальное ускорение в момент
времени 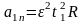 .
В итоге отношение нормального ускорения
к тангенциальному в момент времени
.
В итоге отношение нормального ускорения
к тангенциальному в момент времени
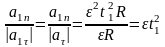 (видно, что для ответа на поставленный
вопрос заданное в условии значение
(видно, что для ответа на поставленный
вопрос заданное в условии значение 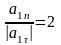 .
.
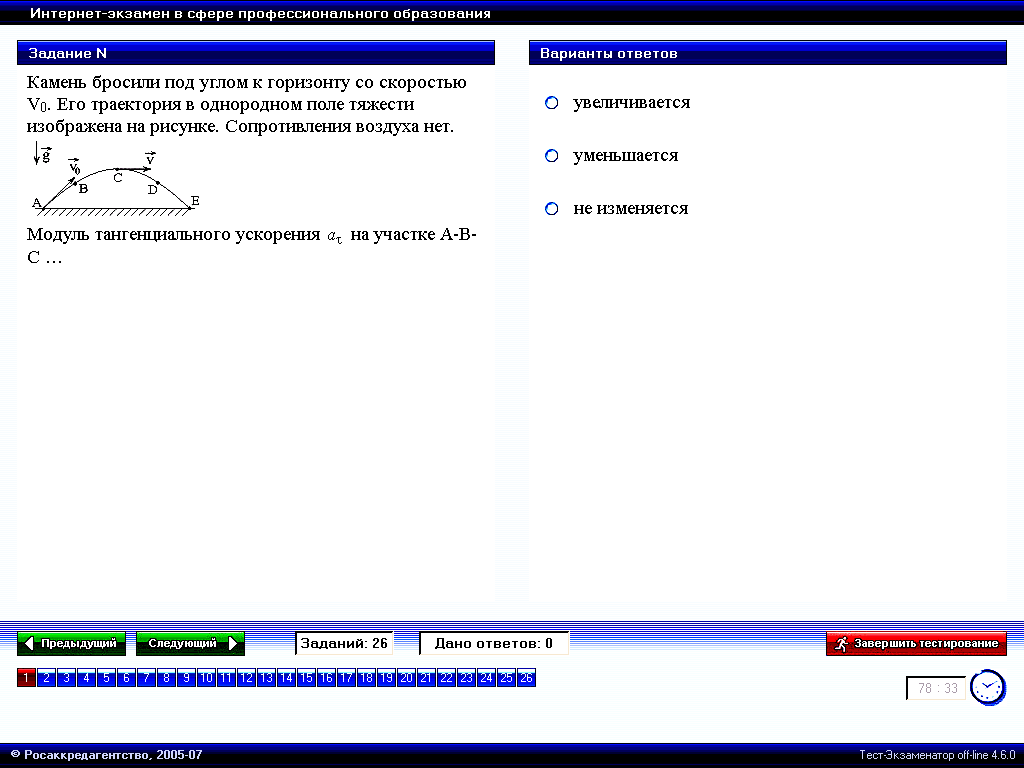
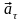 на участке А-В-С …
на участке А-В-С …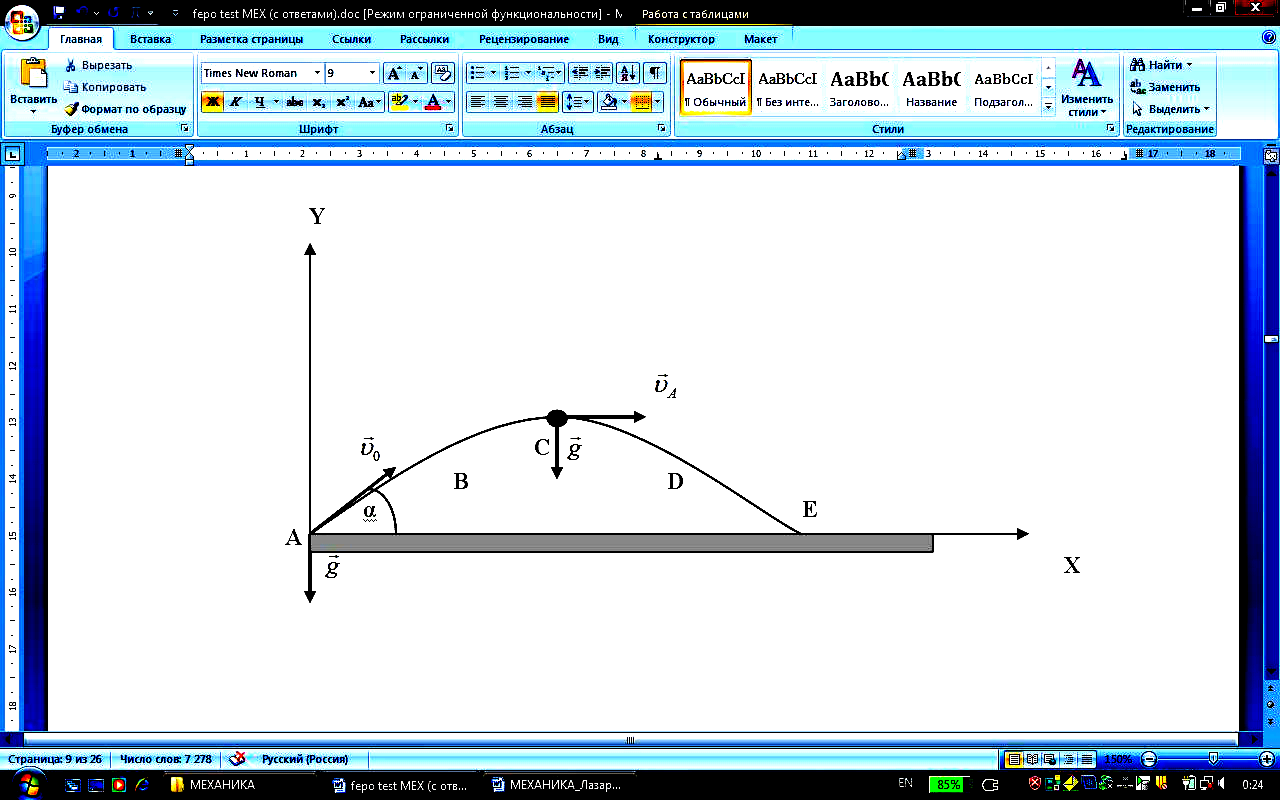 ыберем
направление единичного вектора касания
ыберем
направление единичного вектора касания
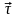 совпадающим с направлением скорости
(тогда
совпадающим с направлением скорости
(тогда
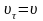 ).
Тогда проекция тангенциального
ускорения
).
Тогда проекция тангенциального
ускорения
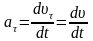 .
Запишем для данного случая уравнения
движения и уравнения для проекций
скорости камня при координатном
способе при выборе декартовых осей
координат, указанном на рисунке:
.
Запишем для данного случая уравнения
движения и уравнения для проекций
скорости камня при координатном
способе при выборе декартовых осей
координат, указанном на рисунке: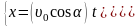
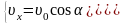
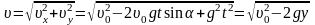
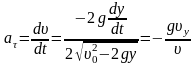 .
Для модуля тангенциального ускорения
получаем:
.
Для модуля тангенциального ускорения
получаем:
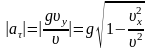 .
(2)
.
(2)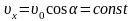 .
На участке А-В-С модуль скорости
уменьшается от
.
На участке А-В-С модуль скорости
уменьшается от
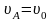 до
до
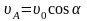 .
Поэтому, исходя из (2), модуль
тангенциального ускорения на участке
А-В-С будет уменьшаться.
.
Поэтому, исходя из (2), модуль
тангенциального ускорения на участке
А-В-С будет уменьшаться. 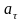
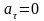
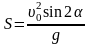 .
Тогда:
.
Тогда:
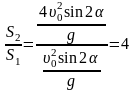 .
.
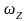 так, как показано на рисунке.
так, как показано на рисунке.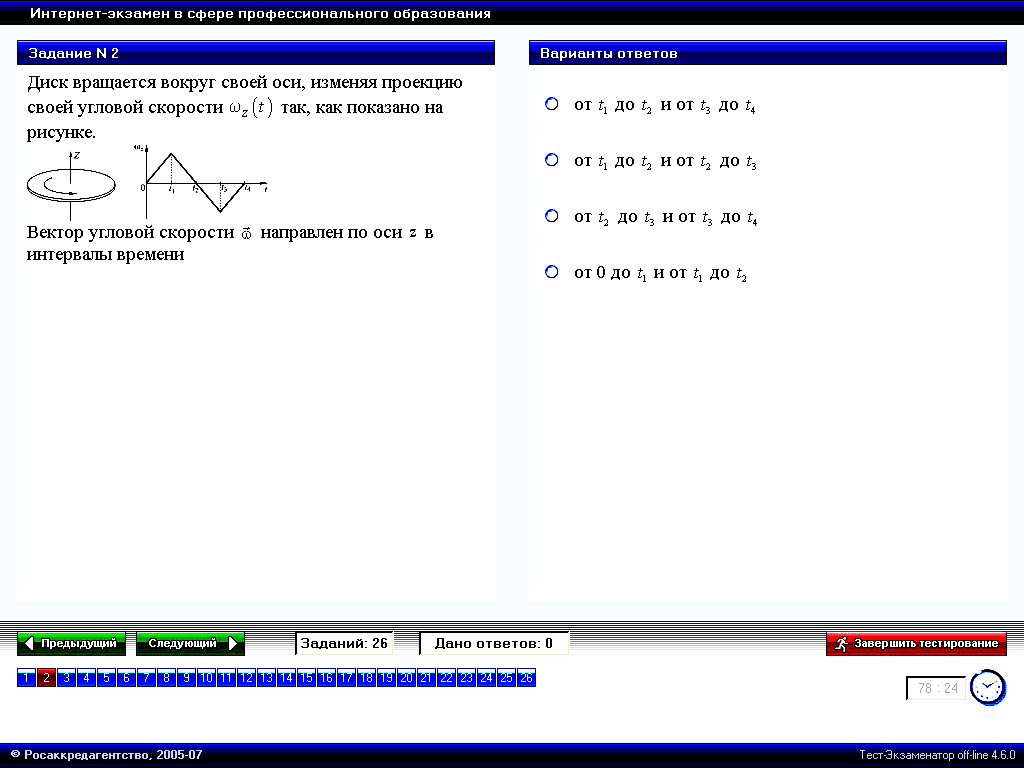
 удем
считать, что диск вращается по часовой
стрелке, если смотреть на него сверху.
Для этого случая направление его
вращения указано стрелкой на рисунке.
Тогда его угловая скорость будет
направлена вертикально вниз. При
равноускоренном движении направление
углового ускорения будет совпадать
с направлением угловой скорости – в
данном случае угловое ускорение будет
направлено вертикально вниз или по
направлению 4.
удем
считать, что диск вращается по часовой
стрелке, если смотреть на него сверху.
Для этого случая направление его
вращения указано стрелкой на рисунке.
Тогда его угловая скорость будет
направлена вертикально вниз. При
равноускоренном движении направление
углового ускорения будет совпадать
с направлением угловой скорости – в
данном случае угловое ускорение будет
направлено вертикально вниз или по
направлению 4.  .
Укажите направление вектора линейной
скорости
.
Укажите направление вектора линейной
скорости
 .
.
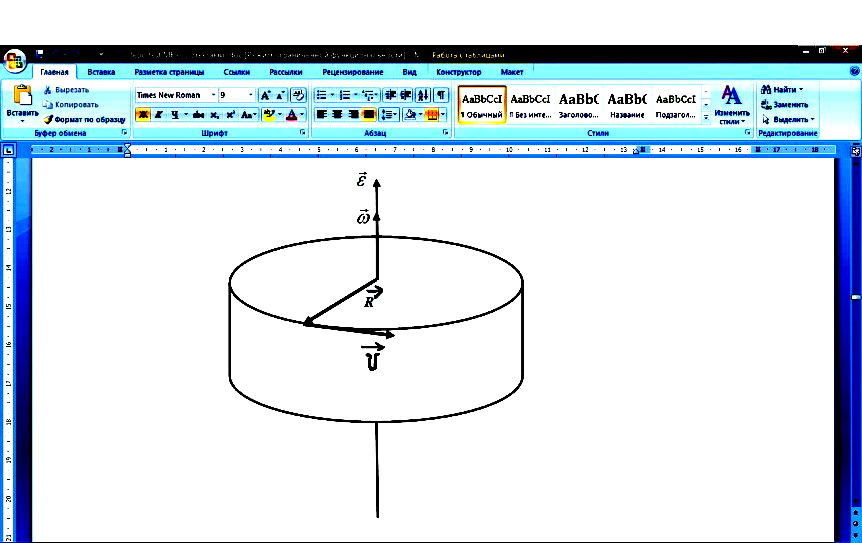 ри
равноускоренном движении направление
угловой скорости
ри
равноускоренном движении направление
угловой скорости
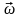 совпадает с направлением углового
ускорения
совпадает с направлением углового
ускорения
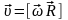 или направление 2 в данном случае.
или направление 2 в данном случае.
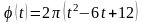 ,
где φ
– в радианах, t
– в секундах. Число оборотов, совершенных
частицей до остановки, равно…
,
где φ
– в радианах, t
– в секундах. Число оборотов, совершенных
частицей до остановки, равно…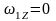 или
или
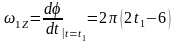 .
Отсюда
.
Отсюда 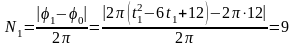 .
.
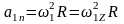 (
(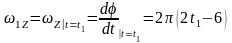 .
После подстановки имеем
.
После подстановки имеем
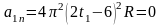 .
.
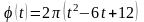 ,
где φ
– в радианах, t
– в секундах. Тангенциальное ускорение
частицы (в м/с2)
через 3 с после начала движения равно…
,
где φ
– в радианах, t
– в секундах. Тангенциальное ускорение
частицы (в м/с2)
через 3 с после начала движения равно…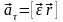 .
Отсюда следует, что модуль тангенциального
ускорения
.
Отсюда следует, что модуль тангенциального
ускорения
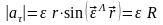 ,
где
,
где 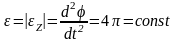 .
Отсюда следует, что модуль углового
ускорения есть величина постоянная
и в момент времени
.
Отсюда следует, что модуль углового
ускорения есть величина постоянная
и в момент времени 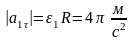 .
.
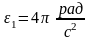 .
.
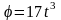 .
Его угловое ускорение через 1 с от
начала движения равно…
.
Его угловое ускорение через 1 с от
начала движения равно…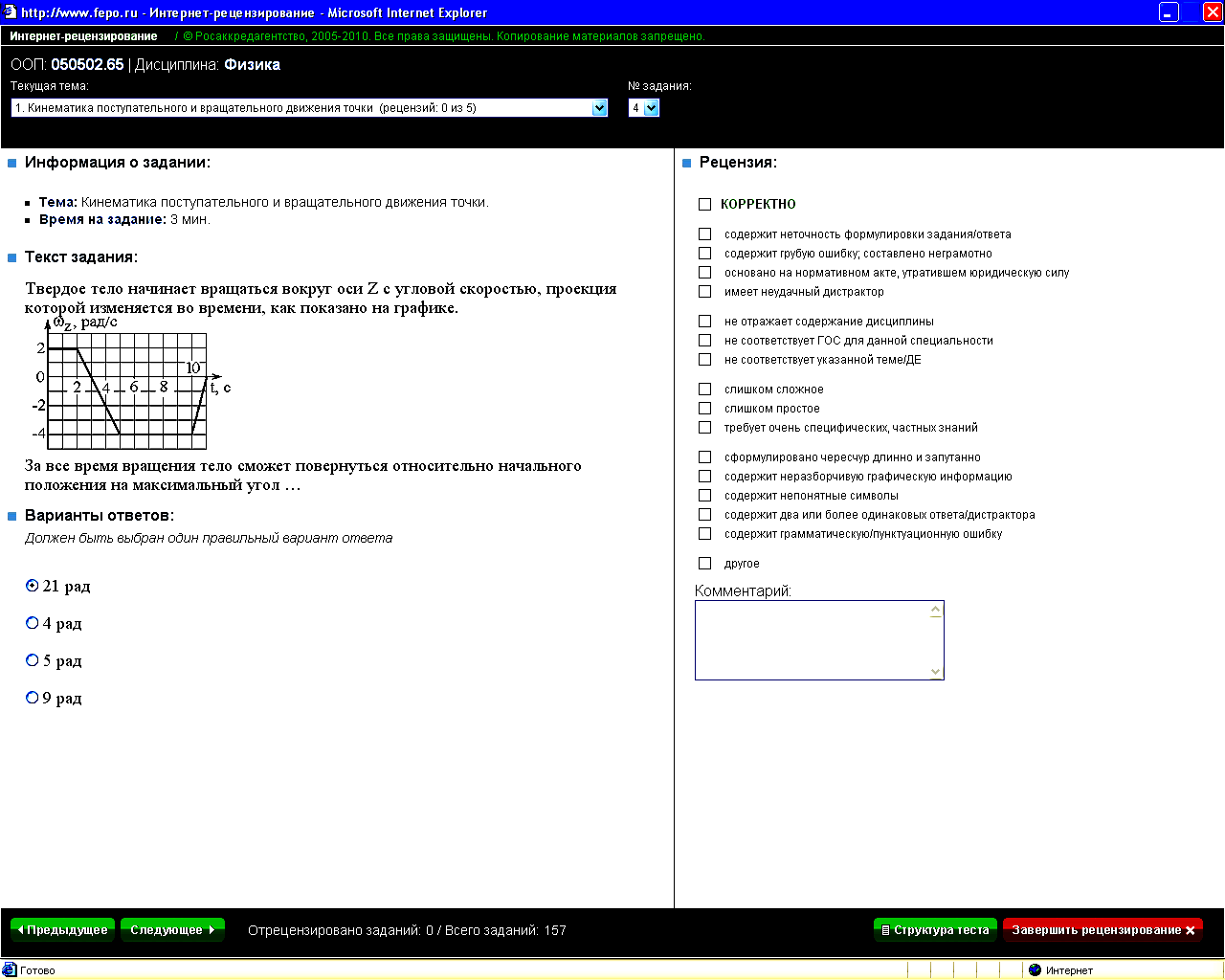
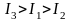
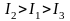
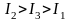
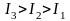
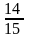
 .
.
 .
Укажите в данной точке направление
вектора скорости, связанной только с
вращением обруча.
.
Укажите в данной точке направление
вектора скорости, связанной только с
вращением обруча.