ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 31.01.2019
Просмотров: 48260
Скачиваний: 391
|
1) 0,003t+0,001t2 |
2) 3+2t |
3) 30t+10t2 |
4) 0,3t+0,1t2 |
|
5.
Материальная
точка M
движется по окружности со скоростью
|
|
||
|
1)
|
2)
|
3)
|
|
|
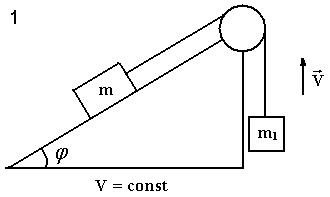
6. Какое из уравнений описывает движение тела m? 1)
|
|
|||
|
7. Вдоль оси OX навстречу друг другу движутся 2 частицы. Их параметры: m1=1г, m2=2г, V1=5м/с, V2=4м/с. Как направлена скорость центра масс системы? |
|
|||
|
1) вправо |
2) Vс = 0 |
3) влево |
||
|
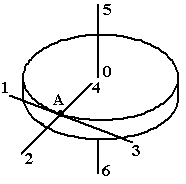
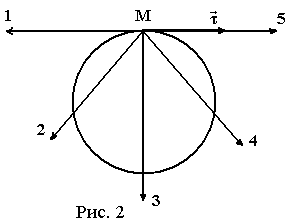
8.
Снаряд разорвался
на 2 осколка, импульсы которых направлены
вдоль линий 3 и 6. Укажите направление
полета снаряда до разрыва, если
|
|
|||||||
|
1) 7 |
2) 5 |
3) 1 |
4) 3 |
5) 2 |
6) 4 |
7) 8 |
8) 6 |
|
|
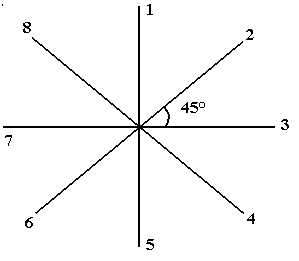
9. Точка М движется по спирали с постоянной по величине скоростью. При этом величина полного ускорения 1)
не изменяется |
|
|
10. Диск радиуса R вращается вокруг вертикальной оси равноускоренно по часовой стрелке. Укажите направление вектора углового ускорения. |
|
||||
|
1) 6 |
2) 3 |
3) 1 |
4) 5 |
5) 2 |
6) 4 |
|
11.
Обруч катится
равномерно со скоростью
|
|
|||||||
|
1) 2 |
2) 1 |
3) 8 |
4) 3 |
5) 4 |
6) 7 |
7) 6 |
8) 5 |
|
12. Колесо радиусом 10 см вращается вокруг неподвижной оси. Зависимость линейной скорости точек на ободе колеса от времени задается уравнением V=3t+t2 (см/с). Чему равно отношение нормального ускорения к тангенциальному при t=1c (в системе СИ)?
|
1) 3,1 |
2) 32 |
3) 0,031 |
4) 0,32 |
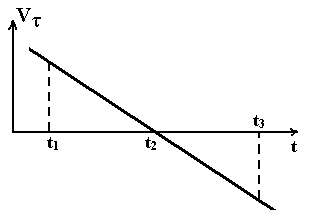
13.
Материальная точка
M
движется по окружности со скоростью
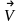 .
На рисунке 1 показан график зависимости
Vτ
от времени. Здесь
.
На рисунке 1 показан график зависимости
Vτ
от времени. Здесь
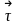 – единичный вектор, указывающий
направление движения (рис. 2). Каково
направление силы, действующей на т.М в
момент времени t1?
– единичный вектор, указывающий
направление движения (рис. 2). Каково
направление силы, действующей на т.М в
момент времени t1?
|
|
|
||||
|
1) 4 |
2) 3 |
3) 2 |
4) 1 |
5) 5 |
|
|
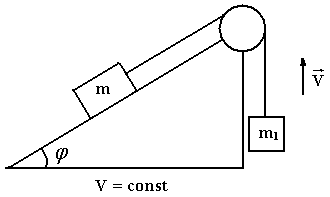
14. Какое соотношение для сил натяжения нитей справедливо? ( Рассматривать для тела на наклонной плоскости!!!) 1)
T1=T2>T3 |
|
|
|
|
|
15. Вдоль оси OX навстречу друг другу движутся 2 частицы. Их параметры: m1=1г, m2=2г, V1=5м/с, V2=4м/с. Чему равна проекция скорости центра масс на ось ОХ (в СИ)? |
|
||
|
1) -1 |
2)
|
3) 0 |
4) 1 |
|
16.
Снаряд разорвался
на 2 осколка, причём импульс снаряда
был направлен вдоль линии 5, а импульс
1-го осколка – вдоль линии 3. Укажите
направление полёта 2-го осколка, если
|
|
|||||||
|
1) 7 |
2) 8 |
3) 6 |
4) 2 |
5) 4 |
6) 5 |
7) 1 |
8) 3 |
|
Правильные ответы
|
Задание № |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
Ответ |
2 |
2 |
3 |
4 |
3 |
2 |
3 |
2 |
3 |
1 |
1 |
4 |
3 |
3 |
1 |
3 |
-
1. 2 м/с
-
2. 3
-
3. 1
-
4. 1
-
5. Ус = 0
-
6) 14
7) у кольца -
8) 5 м/с 9) 3 и 4 10) 3/6 11) 5/6 12) 2 13)4 14)3 или 7/9
-
15) 2 и 3 16) 4 17) 3
-
18) B и D 19)Е(А)>E(B) 20) 4 21)1,75 влево 3 вариант
-
22?
-
23) 3 24)3
25) 1
26) A B C -
27-4;30-3
Ф1.2.2-1
|
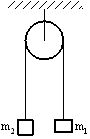
Два тела массами m1 и m2 соединены нерастяжимой нитью, перекинутой через невесомый блок.
Если m1 < m2, а Т – сила натяжения нити, то уравнение второго закона Ньютона для тела массой m1 в проекции на направление движения имеет вид… |
1:
2:
3:
|
|
Так
как m1<m2,
то из состояния покоя тело массой m1
будет двигаться вертикально вверх.
Ускорение тела m1
будет также направлено вертикально
вверх. На тело m1
действуют две силы: сила тяжести
|
|
Ф1.2.2-2
|
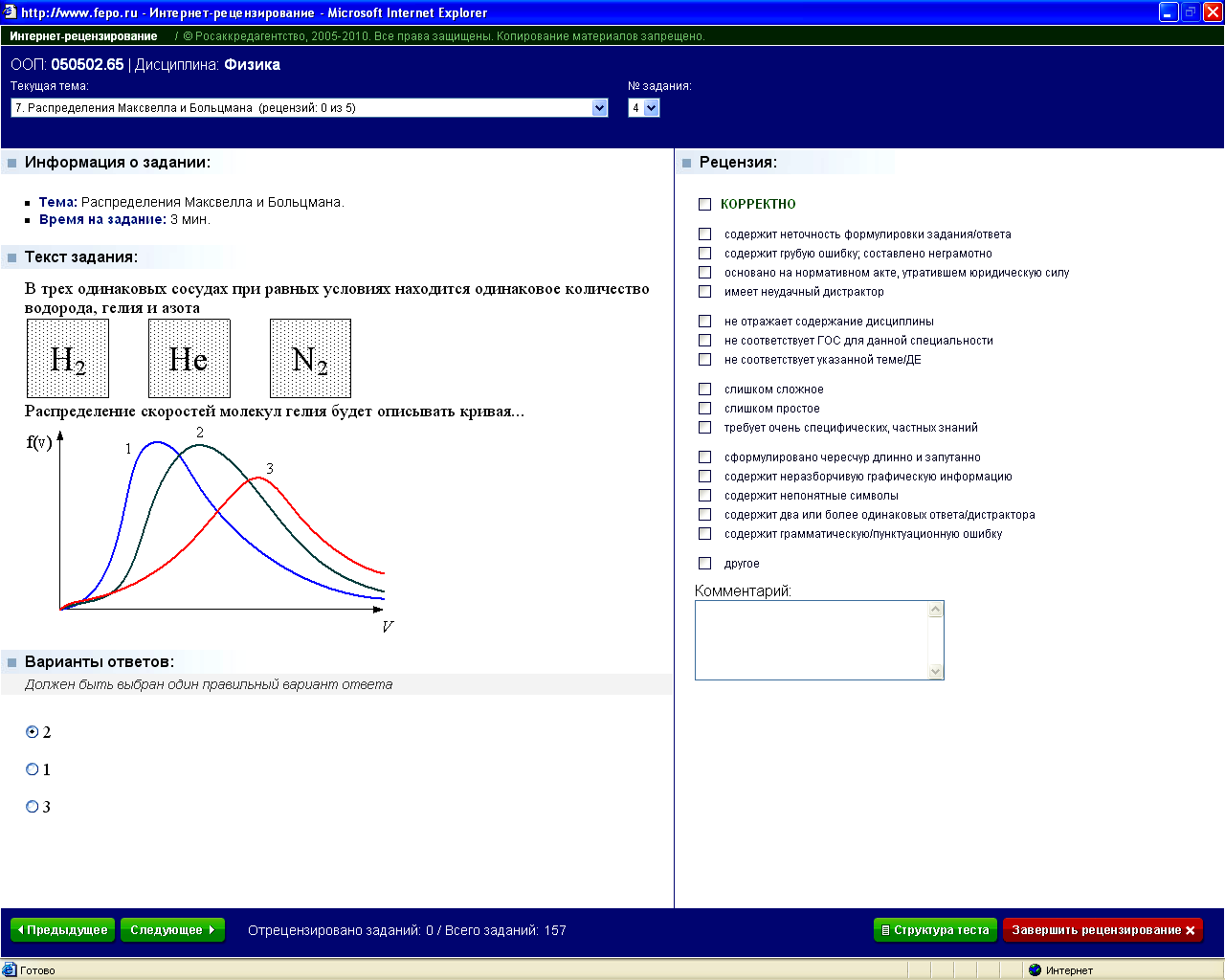
Два тела массами m1 и m2 соединены нерастяжимой нитью, перекинутой через невесомый блок.
Если m1 > m2, а Т – сила натяжения нити, то уравнение второго закона Ньютона для тела массой m2 в проекции на направление движения имеет вид… |
1:
2:
3:
|
|
Так
как m1>m2,
то из состояния покоя тело массой m2
будет двигаться вертикально вверх.
Ускорение тела m2
будет также направлено вертикально
вверх. На тело m2
действуют две силы: сила тяжести
|
|
Ф1.2.2-3
|
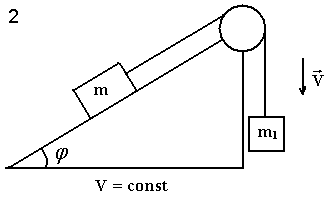
Два тела массами m1 и m2 соединены нерастяжимой нитью, перекинутой через невесомый блок.
Если m1 < m2, а Т – сила натяжения нити, то уравнение второго закона Ньютона для тела массой m2 в проекции на направление движения имеет вид… |
1:
2:
3:
|
|
Так
как m1<m2,
то из состояния покоя тело массой m2
будет двигаться вертикально вниз.
Ускорение тела m2
будет также направлено вертикально
вниз. На тело m2
действуют две силы: сила тяжести
|
|
Ф1.2.2-4
|
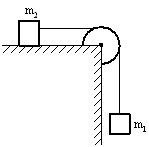
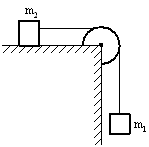
Два тела массами m1 и m2 соединены нерастяжимой нитью, перекинутой через невесомый блок, укрепленный на краю стола с гладкой поверхностью.
Если m1 > m2, а Т – сила натяжения нити, то уравнение второго закона Ньютона для тела массой m1 в проекции на направление движения имеет вид… |
1:
2:
3:
|
|
Вне
зависимости от соотношения масс m1
и m2
из состояния покоя тело массой m1
будет двигаться вертикально вниз.
Ускорение тела m1
будет также направлено вертикально
вниз. На тело m1
действуют две силы: сила тяжести
|
|
Ф1.2.2-5
|
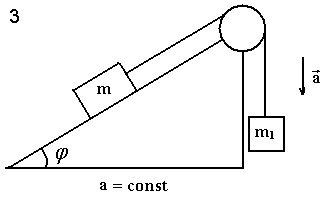
Два тела массами m1 и m2 соединены нерастяжимой нитью, перекинутой через невесомый блок, укрепленный на краю стола с гладкой поверхностью.
Если m1 > m2, а Т – сила натяжения нити, то уравнение второго закона Ньютона для тела массой m2 в проекции на направление движения имеет вид… |
1:
2:
3:
|
|
Вне
зависимости от соотношения масс m1
и m2
из состояния покоя тело массой m2
будет двигаться вправо. Ускорение
тела m2
будет также направлено вправо. На тело
m2
действуют две силы: сила тяжести
|
|
2.1.1-1
|
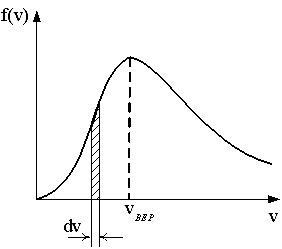
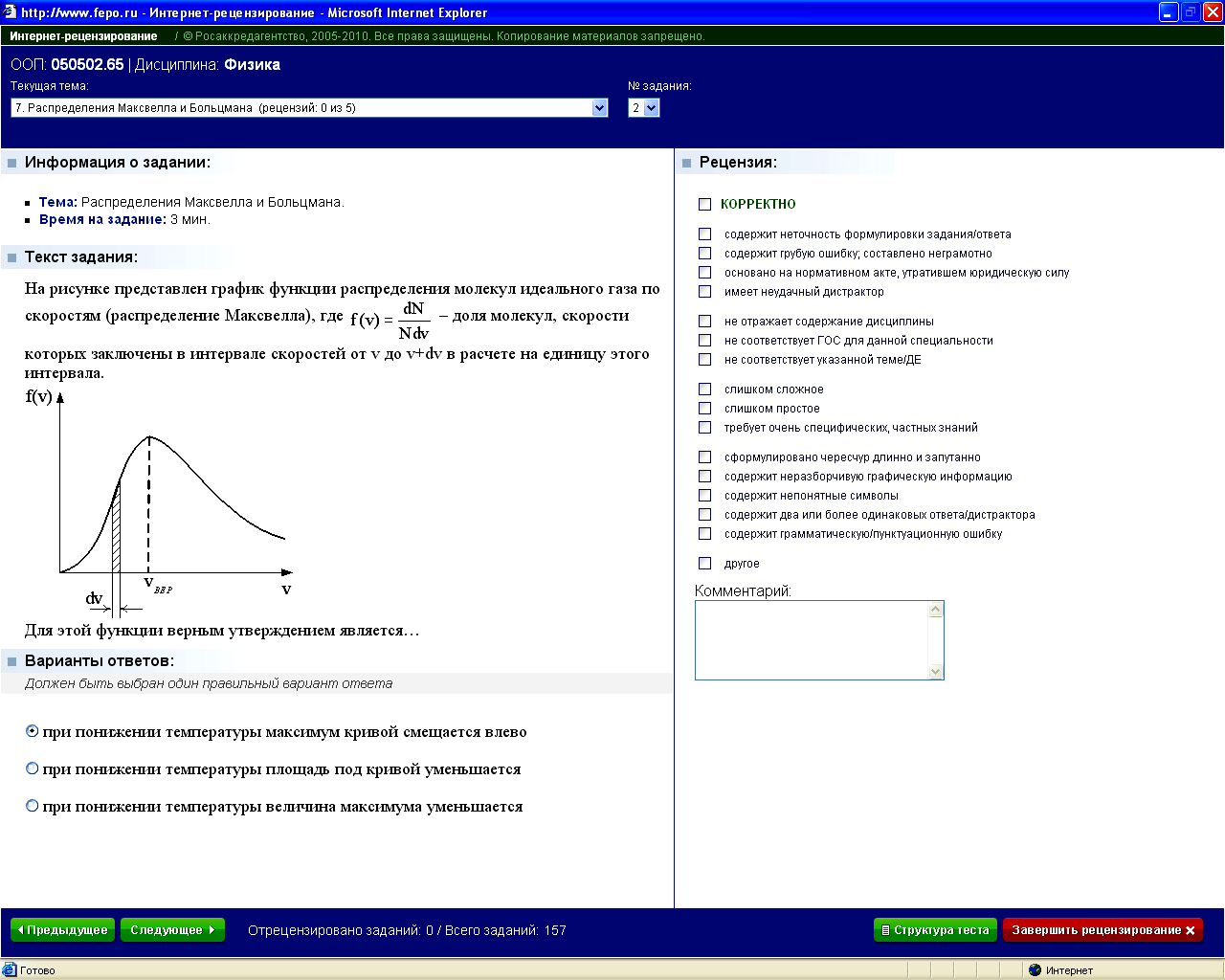
На
рисунке представлен график функции
распределения молекул идеального
газа по скоростям (распределение
Максвелла), где
|
1. С ростом температуры площадь под кривой растёт. 2. С ростом температуры величина максимума растёт. 3. С ростом температуры максимум кривой смещается вправо.* |
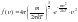 – функция
распределения Максвелла по абсолютным
скоростям. Условие нормировки для
функции распределения имеет вид
– функция
распределения Максвелла по абсолютным
скоростям. Условие нормировки для
функции распределения имеет вид
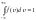 .
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
.
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
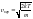 – соответствует максимуму кривой.
Отсюда следует, что
– соответствует максимуму кривой.
Отсюда следует, что
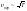 .
То есть с ростом температуры максимум
кривой смещается вправо. При этом, с
учётом вышесказанного, величина максимума
будет уменьшаться.
.
То есть с ростом температуры максимум
кривой смещается вправо. При этом, с
учётом вышесказанного, величина максимума
будет уменьшаться.
Ответ: 3
2.1.1-2
|
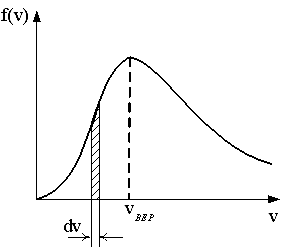
На
рисунке представлен график функции
распределения молекул идеального
газа по скоростям (распределение
Максвелла), где
|
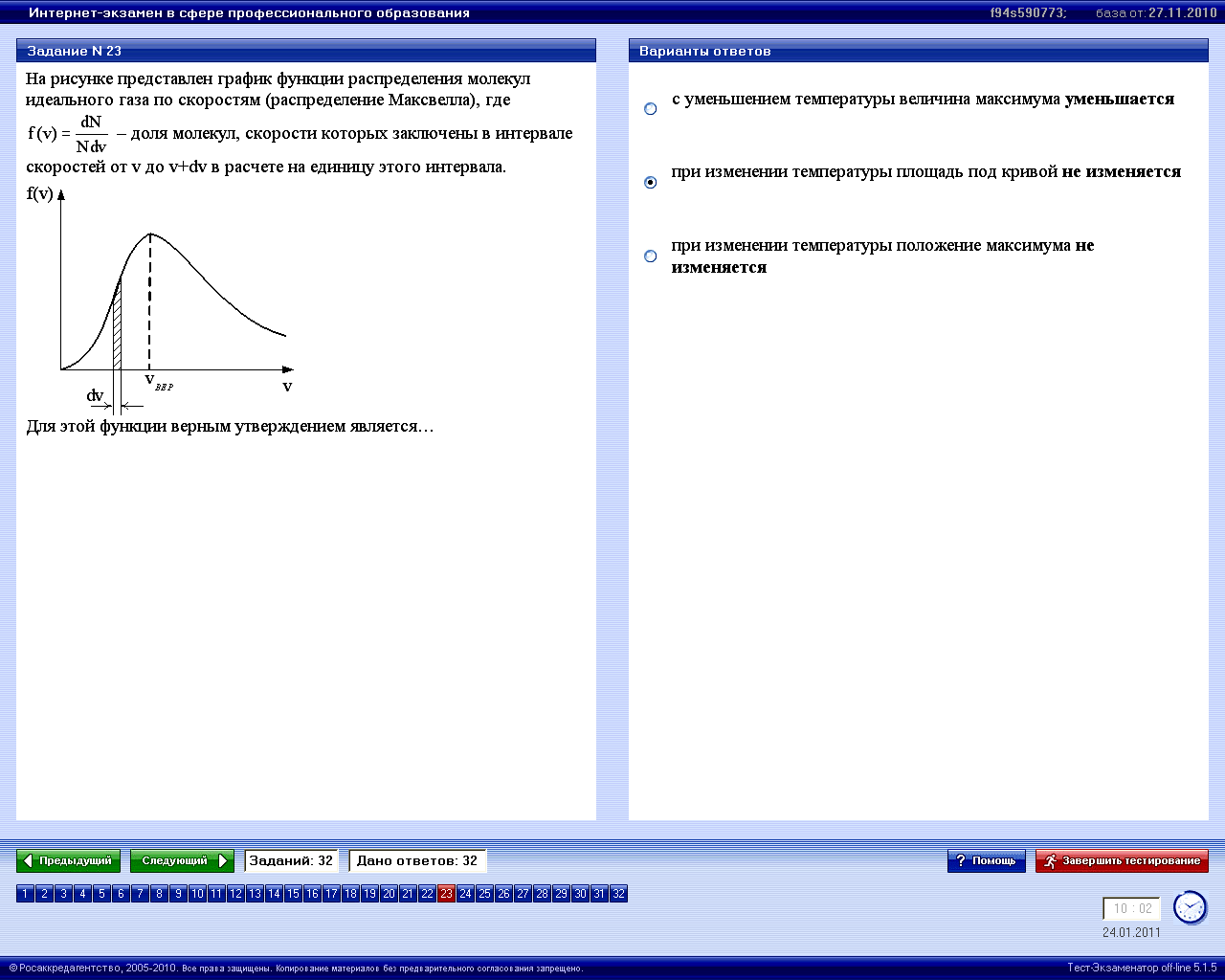
1: С ростом температуры максимум кривой смещается вправо.* 2: При любом изменении температуры площадь под кривой не изменяется.* 3: Площадь заштрихованной полоски равна числу молекул со скоростями в интервале от v до v+dv. |
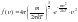 – функция
распределения Максвелла по абсолютным
скоростям. Условие нормировки для
функции распределения имеет вид
– функция
распределения Максвелла по абсолютным
скоростям. Условие нормировки для
функции распределения имеет вид
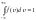 .
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
.
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
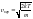 – соответствует максимуму кривой.
Отсюда следует, что
– соответствует максимуму кривой.
Отсюда следует, что
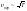 .
То есть с ростом температуры максимум
кривой смещается вправо. Площадь
заштрихованной полоски равна доле
молекул, а не числу молекул, скорости
которых заключены в интервале скоростей
от v до v+dv.
.
То есть с ростом температуры максимум
кривой смещается вправо. Площадь
заштрихованной полоски равна доле
молекул, а не числу молекул, скорости
которых заключены в интервале скоростей
от v до v+dv.
Ответы: 1, 2
2.1.1-3
|
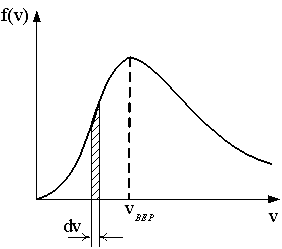
На
рисунке представлен график функции
распределения молекул идеального
газа по скоростям (распределение
Максвелла), где
|
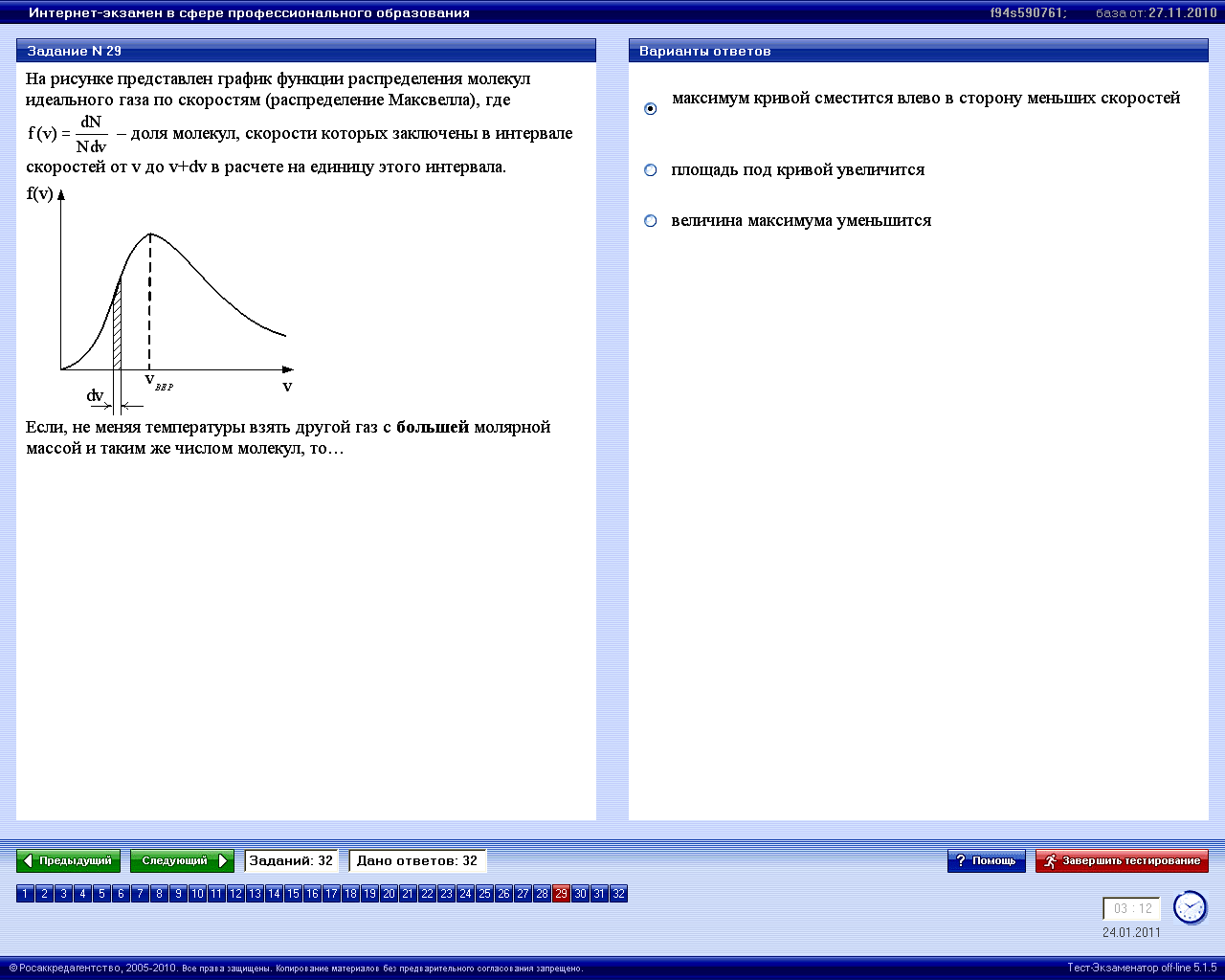
1: Площадь заштрихованной полоски равна доле молекул со скоростями в интервале от v до v+dv.* 2: При понижении температуры максимум кривой смещается влево.* 3: При понижении температуры площадь под кривой уменьшается. |
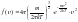 – функция
распределения Максвелла по абсолютным
скоростям. Условие нормировки для
функции распределения имеет вид
– функция
распределения Максвелла по абсолютным
скоростям. Условие нормировки для
функции распределения имеет вид
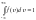 .
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
.
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
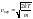 – соответствует максимуму кривой.
Отсюда следует, что
– соответствует максимуму кривой.
Отсюда следует, что
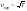 .
То есть при понижении температуры
максимум кривой смещается влево. Площадь
заштрихованной полоски равна доле
молекул, скорости которых заключены в
интервале скоростей от v до v+dv.
.
То есть при понижении температуры
максимум кривой смещается влево. Площадь
заштрихованной полоски равна доле
молекул, скорости которых заключены в
интервале скоростей от v до v+dv.
Ответы: 1, 2
2.1.1-4
|
На
рисунке представлен график функции
распределения молекул идеального
газа по скоростям (распределение
Максвелла), где
|
1: С ростом температуры максимум кривой смещается вправо.* 2: С ростом температуры площадь кривой не изменяется.* 3: Вид функции распределения не зависит от природы газа (от массы молекул). |
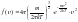 – функция
распределения Максвелла по абсолютным
скоростям, где m
– масса молекулы, что означает, что вид
функции распределения зависит от природы
газа (от массы молекул). Условие нормировки
для функции распределения имеет вид
– функция
распределения Максвелла по абсолютным
скоростям, где m
– масса молекулы, что означает, что вид
функции распределения зависит от природы
газа (от массы молекул). Условие нормировки
для функции распределения имеет вид
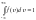 .
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
.
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
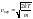 – соответствует максимуму кривой.
Отсюда следует, что
– соответствует максимуму кривой.
Отсюда следует, что
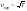 .
То есть с ростом температуры максимум
кривой смещается вправо.
.
То есть с ростом температуры максимум
кривой смещается вправо.
Ответы: 1, 2
2.1.1-5
|
На
рисунке представлен график функции
распределения молекул идеального
газа по скоростям (распределение
Максвелла), где
|
1: При понижении температуры максимум кривой смещается влево.* 2: При любом изменении температуры площадь под кривой не изменяется.* 3: Площадь заштрихованной полоски равна числу молекул со скоростями в интервале v до v+dv. |
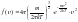 – функция
распределения Максвелла по абсолютным
скоростям. Условие нормировки для
функции распределения имеет вид
– функция
распределения Максвелла по абсолютным
скоростям. Условие нормировки для
функции распределения имеет вид
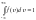 .
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
.
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
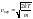 – соответствует максимуму кривой.
Отсюда следует, что
– соответствует максимуму кривой.
Отсюда следует, что
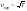 .
То есть при понижении температуры
максимум кривой смещается влево. Площадь
заштрихованной полоски равна доле
молекул, а не числу молекул, скорости
которых заключены в интервале скоростей
от v до v+dv.
.
То есть при понижении температуры
максимум кривой смещается влево. Площадь
заштрихованной полоски равна доле
молекул, а не числу молекул, скорости
которых заключены в интервале скоростей
от v до v+dv.
Ответы: 1, 2
2.1.1-6
|
На
рисунке представлен график функции
распределения молекул идеального
газа по скоростям (распределение
Максвелла), где
|
1: Положение максимума кривой зависит как от температуры, так и от природы газа.* 2: При понижении температуры максимум кривой смещается влево.* 3: При понижении температуры площадь под кривой уменьшается. |
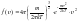 – функция
распределения Максвелла по абсолютным
скоростям, где m
– масса молекулы, Т
– температура газа. Это означает, что
вид функции распределения зависит от
природы газа (от массы молекул) и
температуры газа. Условие нормировки
для функции распределения имеет вид
– функция
распределения Максвелла по абсолютным
скоростям, где m
– масса молекулы, Т
– температура газа. Это означает, что
вид функции распределения зависит от
природы газа (от массы молекул) и
температуры газа. Условие нормировки
для функции распределения имеет вид
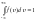 .
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
.
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры. Наиболее
вероятная скорость, соответствующая
максимуму кривой,
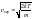 – соответствует максимуму кривой.
Отсюда следует, что
– соответствует максимуму кривой.
Отсюда следует, что
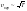 .
То есть при понижении температуры
максимум кривой смещается влево.
.
То есть при понижении температуры
максимум кривой смещается влево.
Ответы: 1, 2
2.1.1-7
|
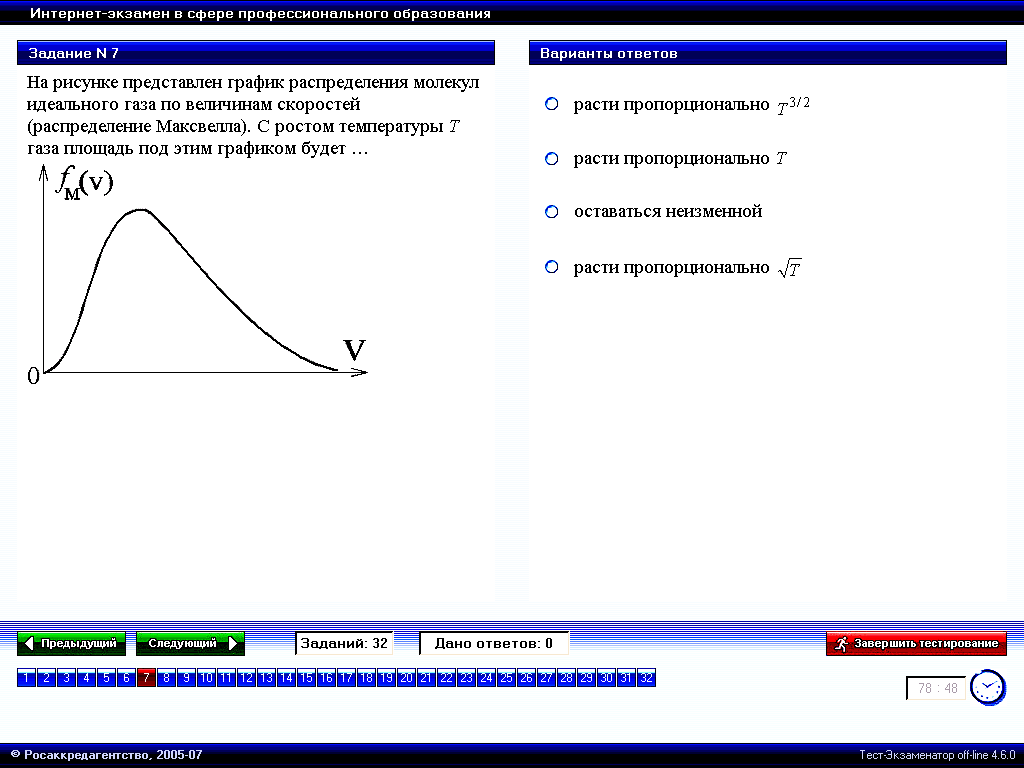
На рисунке представлен график распределения молекул идеального газа по величинам скоростей (распределение Максвелла). С ростом температуры Т газа площадь под этим графиком будет …
|
1.
расти пропорционально
2.
расти пропорционально
3. оставаться неизменной* 4.
расти пропорционально
|
Условие
нормировки для функции распределения
имеет вид
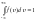 .
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры.
.
Это означает, что площадь под кривой
всегда равно единице и не изменяется
при изменении температуры.
Ответ: 3
2.1.1-8
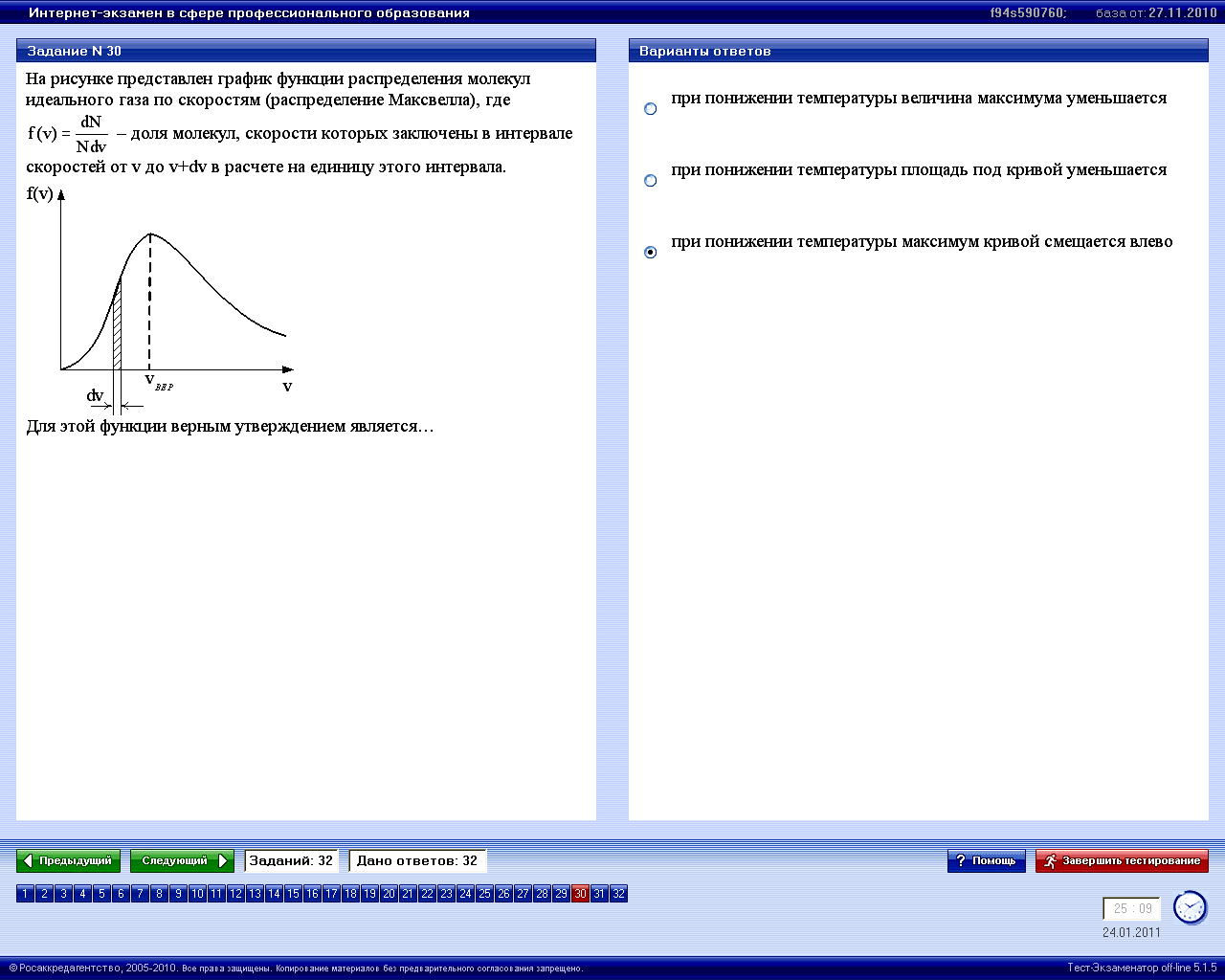
2.1.1-9
2.1.1-10
2.1.1-11
2.1.1-12
|
|
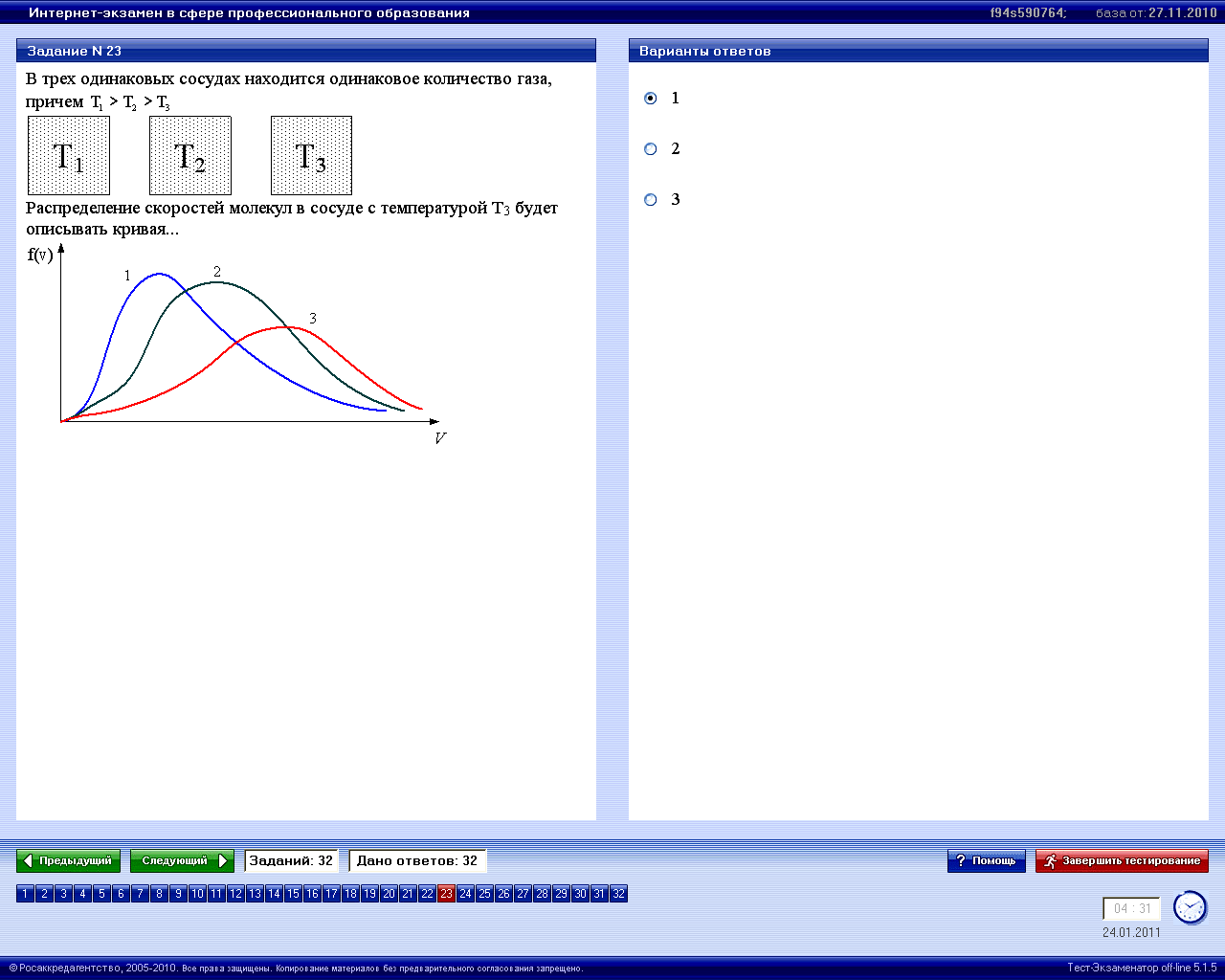
1* |
при понижении температуры максимум кривой смещается влево |
|
2 |
при понижении температуры площадь под кривой уменьшается |
|
|
3 |
при понижении температуры величина максимума уменьшается |
2.1.1-13
|
|
1* |
2 |
|
2 |
1 |
|
|
3 |
3 |
2.3.1-1
|
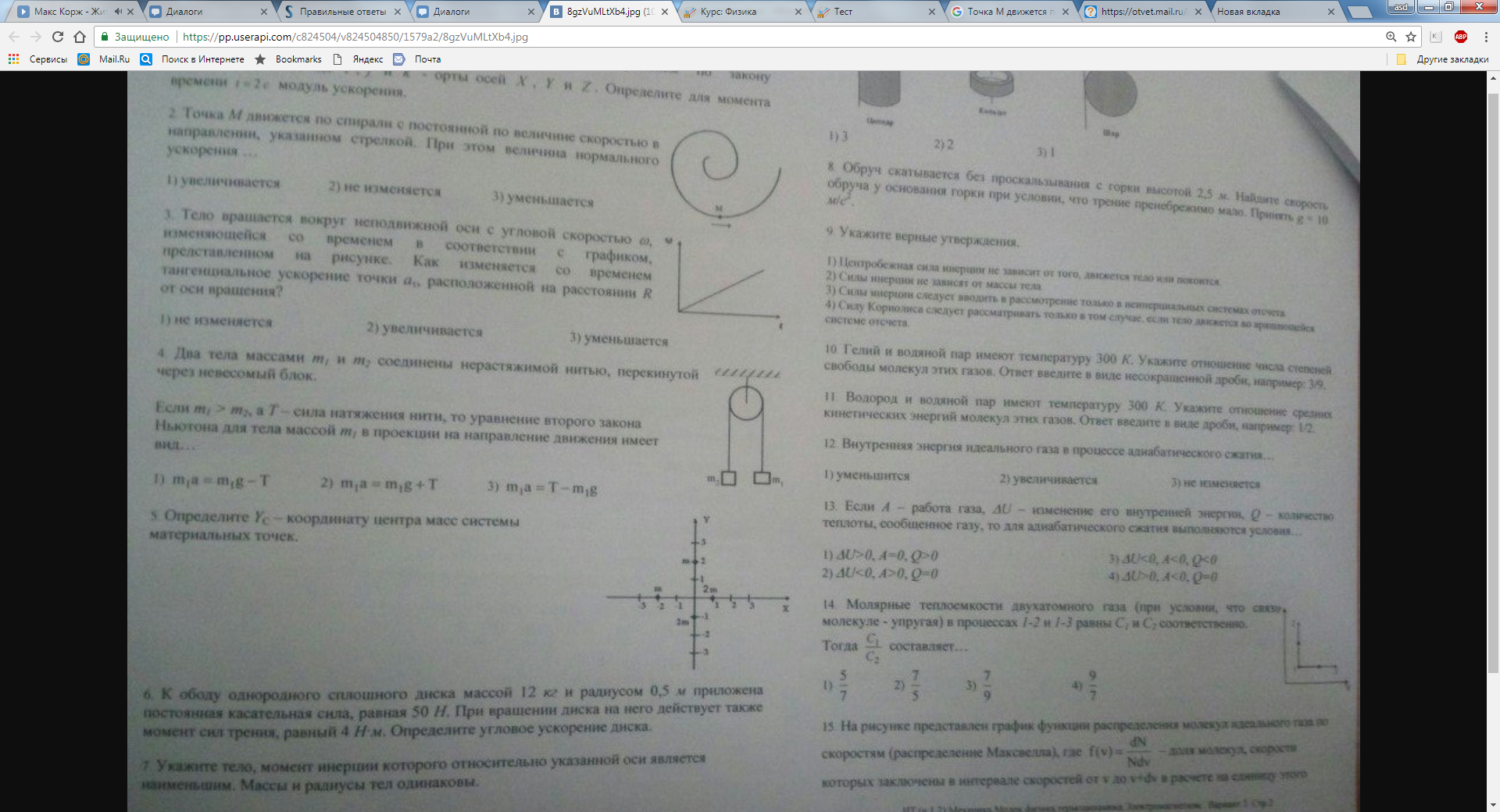
На рисунке изображен цикл Карно в координатах (T,S), где S-энтропия. Теплота подводится к системе на участке …
|
1: 2 – 3 2: 1 – 2* 3: 4 – 1 4: 3 – 4 |
Теплообмен
происходит при изотермическом процессе
(T-const).
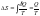 .
Q>0
(подводится
тепло),
S
– возрастает,
.
Q>0
(подводится
тепло),
S
– возрастает,
Q<0 (отводится тепло), S – убывает. Таким образом, теплота подводится к системе на участке 1-2 (T-const, энтропия – возрастает).
Ответ: 2
2.3.1-2
|
На рисунке изображен цикл Карно в координатах (T,S), где S-энтропия. Адиабатное расширение происходит на этапе …
|
1: 2 – 3* 2: 1 – 2 3: 3 – 4 4: 4 – 1 |
Процессы 2-3 и 4-1 являются адиабатными. Адиабатное расширение происходит на этапе уменьшения температуры, т.е. на участке 2 – 3.
Ответ: 1
2.3.1-3
|
На рисунке изображен цикл Карно в координатах (T,S), где S-энтропия. Изотермическое сжатие происходит на этапе …
|
1: 3 – 4* 2: 1 – 2 3: 2 – 3 4: 4 – 1 |
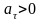
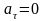
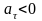
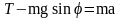
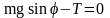
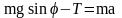
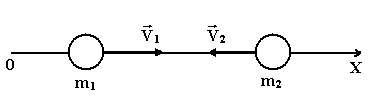
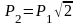 .
.
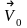 .
Укажите в данной точке направление
вектора полной скорости.
.
Укажите в данной точке направление
вектора полной скорости.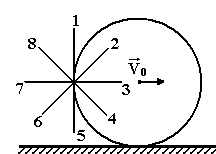
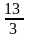
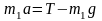 *
*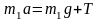
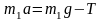
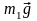 ,
направленная вертикально вниз, и сила
натяжения нити
,
направленная вертикально вниз, и сила
натяжения нити
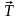 ,
направленная вертикально вверх. Тогда
теорема о движении центра масс тела
,
направленная вертикально вверх. Тогда
теорема о движении центра масс тела
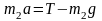 *
*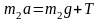
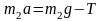
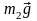 ,
направленная вертикально вниз, и сила
натяжения нити
,
направленная вертикально вниз, и сила
натяжения нити
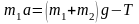
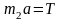 *
*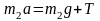
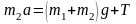
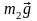 ,
направленная вертикально вниз (проекция
этой силы на направление движения
тела
,
направленная вертикально вниз (проекция
этой силы на направление движения
тела 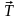 ,
направленная вправо (сила трения на
тело
,
направленная вправо (сила трения на
тело