Добавлен: 31.01.2019
Просмотров: 956
Скачиваний: 11

 МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ХАКАССКИЙ ТЕХНИЧЕСКИЙ ИНСТИТУТ - филиал
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Рабочая тетрадь
Студент __________________________ Группа ______________
Преподаватель__________________________________________
Абакан
ХТИ СФУ
 2013
2013
Обозначения и символы
В рабочей тетради представлены задания для самостоятельного решения. Основную их часть студенты выполняют на занятиях, некоторые по выбору преподавателя – во внеучебное время.
Задания распределены по отдельным темам. Для подготовки к каждой из них студент должен изучить соответствующий материал по конспекту лекций, рекомендуемой учебной литературе и ответить на вопросы, приведенные в начале каждой темы.
Решение каждого задания студент должен выполнять по следующему плану:
1. Внимательно прочитать условие и исходный чертеж. Представить мысленно все заданные геометрические элементы в пространстве.
2. Если необходимо записать алгоритм решения.
3. Выполнить построения на эпюре, соблюдая последовательность запланированных графических операций.
 Графические
построения должны выполняться аккуратно
при помощи чертежных инструментов.
Рекомендуется применять цветные
карандаши. Результат решения задания
должен быть выделен красным цветом.
Буквенные и цифровые обозначения и
запись алгоритмов выполняют по ГОСТ
2.304-81
Графические
построения должны выполняться аккуратно
при помощи чертежных инструментов.
Рекомендуется применять цветные
карандаши. Результат решения задания
должен быть выделен красным цветом.
Буквенные и цифровые обозначения и
запись алгоритмов выполняют по ГОСТ
2.304-81
ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ
|
А,В,С, ... 1, 2, 3, ... |
- точки пространства (буквы прописные латинские, цифры арабские); |
|
а, b, c, ... |
- прямые и кривые линии; |
|
h, f, p |
- горизонтали, фронтали, профильные прямые; |
|
α, β, γ, ... |
- плоскости и поверхности (строчные греческие); |
|
απ1, απ2, απ3 |
- горизонтальный, фронтальный и профильный следы плоскости |
|
П1, П2, П3 |
- горизонтальная, фронтальная, профильная плоскости проекций; |
|
А1, а1, α1, ... |
- горизонтальные проекции точки, линии и плоскости; |
|
А2, а2, α2, ... |
- фронтальные проекции точки, линии и плоскости; |
|
А3, а3, α3, ... |
- профильные проекции точки, линии и плоскости; |
|
К |
- картинная плоскость (прописная); |
|
k |
- основание картины (строчная). |
|
A′ |
- перспективная проекция точки; |
|
A1′ |
- вторичная проекция точки; |
|
Знак |
Значение |
Пример |
Чтение |
|
∈ |
Принадлежность элемента |
A ∈ α |
Точка A принадлежит плоскости α |
|
⊂ |
Принадлежность множества |
a ⊂ β |
Линия a принадлежит плоскости β |
|
∩ |
Пересечение |
a ∩ γ = K |
Линия a пересекается с плоскостью γ в точке K |
|
| | |
Параллельность |
l | | q |
Прямая l параллельна прямой q |
|
⊥ |
Перпендикулярность |
a ⊥b |
Прямая a перпендикулярна прямой b |
|
≡ |
Совпадение, равенство |
K ≡a ∩ φ |
Точка K есть точка пересечения линии a с плоскостью φ |
|
[...] |
Отрезок прямой |
[AB] |
Отрезок прямой, ограниченный точками A и B |
|
| ... | |
Расстояние |
| AB | |
Расстояние между точками A и B |
|
∧ |
Величина угла |
∧ АВС |
Величина угла в градусах |
Тема 1. ТОЧКА И ПРЯМАЯ
Вопросы для подготовки
1. Что называется эпюром Монжа (комплексным чертежом) и как он образу-
ется?
2. Какими координатами определяется положение точки в пространстве?
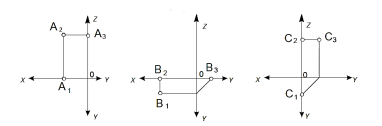
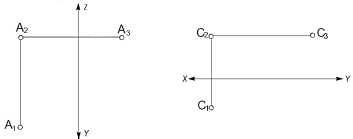
3. Как по двум проекциям точки построить третью?
4. Какие точки называются конкурирующими?
5. Дайте характеристику проекциям прямых частного и общего положения.
6. Как по проекциям прямой общего положения определить ее натуральную
величину и углы наклона ее к плоскостям проекций?
7. Что называется следом прямой на плоскости проекций? Какая координата
равна нулю для горизонтального следа, фронтального следа прямой?
8. В каком случае прямой угол проецируется на плоскость проекций в виде
прямого угла?
Задача 1
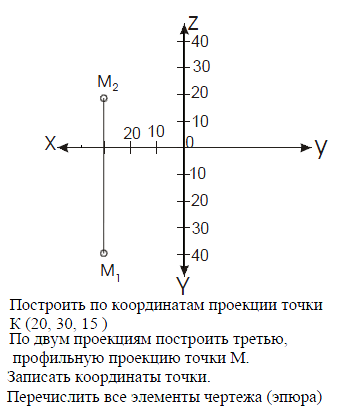
___________________________________________________
___________________________________________________
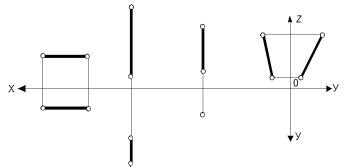
Задача 2
 Построить
по координатам проекции точек А,
В,
С
и D
Построить
по координатам проекции точек А,
В,
С
и D
А(25, 10, 30)
В( 25, 40, 30)
С(
40, 25, 45)
D(
40, 25,10)
Какие точки являются конкурирующими?
 Показать
видимость точек в плоскости П1
и П2
Показать
видимость точек в плоскости П1
и П2
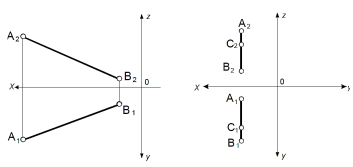
Задача 3
Каким плоскостям проекций принадлежат точки А, В и С? Записать координаты точек.
Задача 4 Задача 5
|
Определить положение оси xy Записать координату точки А |
Определить положение оси zy Записать координату точки С |
Задача 6 Задача 7
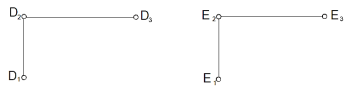
|
Определит положение осей, если точка D отстоит от плоскости П2 на расстоянии 10 мм. Записать координаты точки D |
Определит положение осей, если точка Е отстоит от плоскости П3 на расстоянии 30 мм. Записать координаты точки Е |
Задача 8 Задача 9
|
На отрезке АВ выбрать точку Е, удаленную от П1 на 15 мм. |
Определить, принадлежит ли точка С прямой АВ |
Задача 10 Задача 11
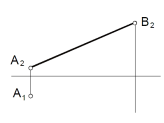
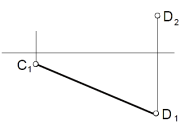
|
Построить недостающую проекцию отрезка АВ если его длина равна 60 мм |
Построить недостающую проекцию отрезка CD, если угол наклона прямой к П1 = 300 |
Задача 12
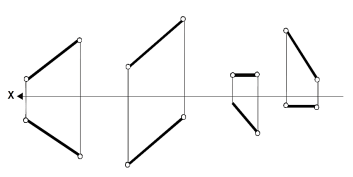
Определить натуральную величину и углы наклона отрезков к плоскостям проекций.
Какое положение занимают эти линии относительно плоскостей проекций?
Задача 13
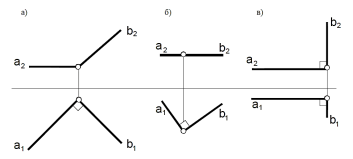
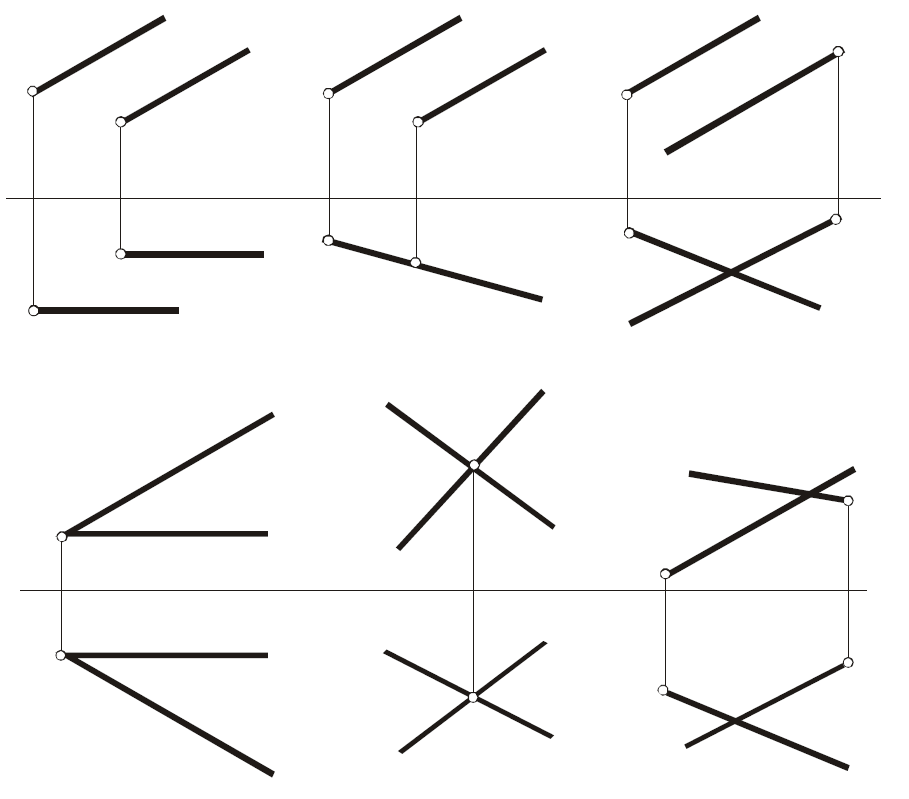
На каких чертежах (а,б,в) прямая а⊥в? Докажите на чертежах.
Задача 14
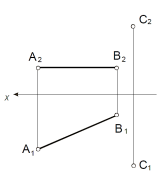
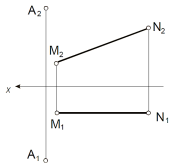
Определить расстояние от Построить квадрат ABCD со
точки С до прямой АВ стороной CD на прямой MN
Задача 15
Определить взаимное положение прямых. На скрещивающихся прямых обозначит конкурирующие точки (или точки кажущегося пересечения). Определить их видимость
Задача 16
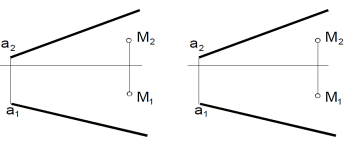
Через точку М провести горизонталь h пересекающую прямую а.
Через точку М провести прямую т параллельную прямой а.
Тема 2. ПЛОСКОСТЬ
Вопросы для подготовки
1. Как можно задать плоскость на чертеже?
2. Какое положение может занимать плоскость относительно плоскостей проекций?
3. Перечислите все виды проецирующих плоскостей
4. Сформулируйте графический признак проецирующей плоскости?
5. Каким свойством обладают плоскости частного положения?
6. Сформулируйте правило принадлежности прямой и точки плоскости.
7. Перечислите и дайте определение главным линиям плоскости. Какие графические признаки используются при построении этих линий?
Задача 17
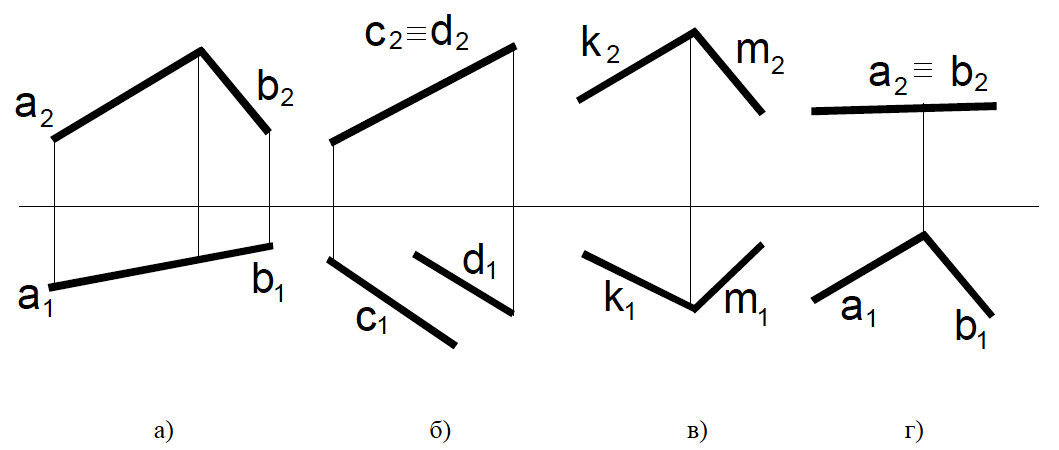
__________________ ________________ ______________ ____________
__________________ ________________ ______________ ____________
Как расположены по отношению к плоскостям проекций плоскости на чертежах? Подписать их названия.
Задача 18 Задача 19
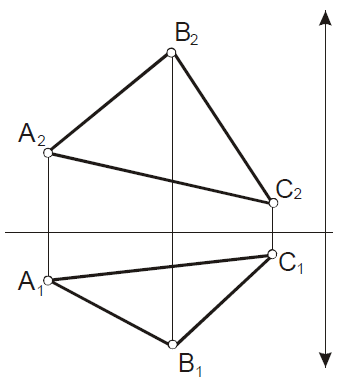
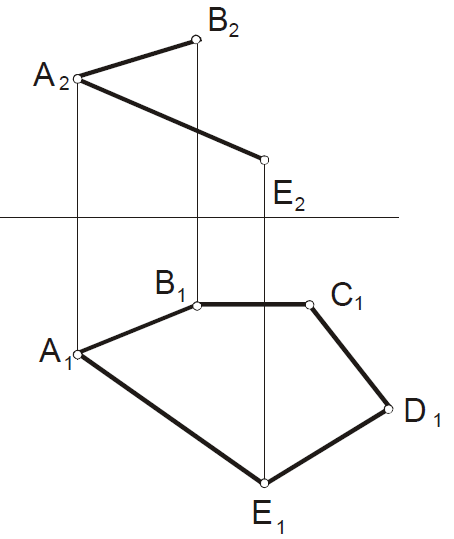
|
Построить недостающие проекции вершин плоского пятиугольника АВСDЕ. |
В плоскости АВС провести горизонталь, удаленную от П1 на 25 мм и фронталь удаленную от П2 на 20мм |
Задача 20
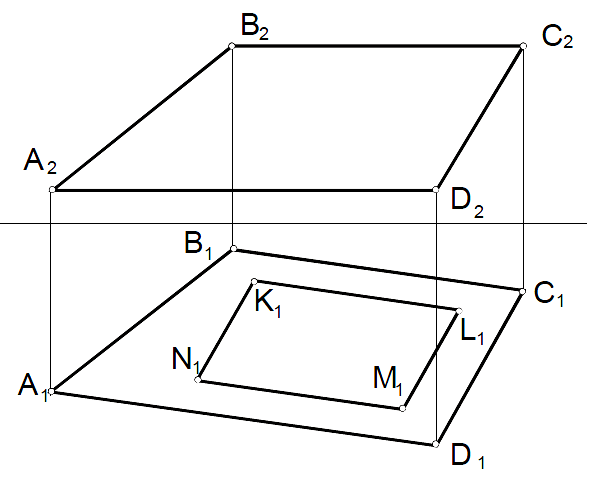
В плоскости ската крыши АВСD размечен четырехугольник для слухового окна KLMN. Построить его недостающую проекцию.
Тема 3.
ИЗОБРАЖЕНИЕ ПЛОСКОСТИ. ПРЯМЫЕ И ТОЧКИ В ПЛОСКОСТИ
Вопросы для подготовки
1. Перечислите возможные случаи взаимного расположения прямой и плоскости.
2. Сформулируйте графический признак параллельности прямой и плоскости
3. Сформулируйте графический признак перпендикулярности прямой и плоскости.
4. Сформулируйте графический признак параллельности плоскостей.
5. Сформулируйте графический признак перпендикулярности плоскостей.
Задача 21
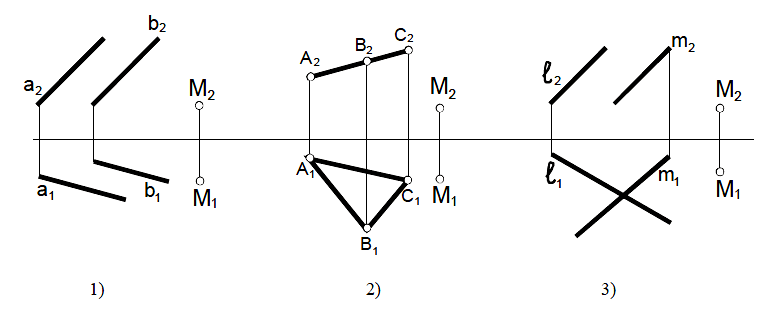
Через точку М провести плоскость, параллельную
1) α(а II b)
2) Δ АВС
3) прямых l и m
Задача 22
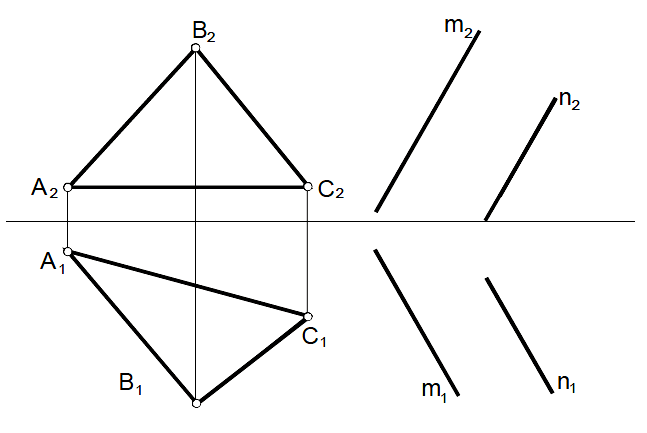
Доказать (графически) параллельность данных плоскостей между собой используя прямые уровня.
Задача 23
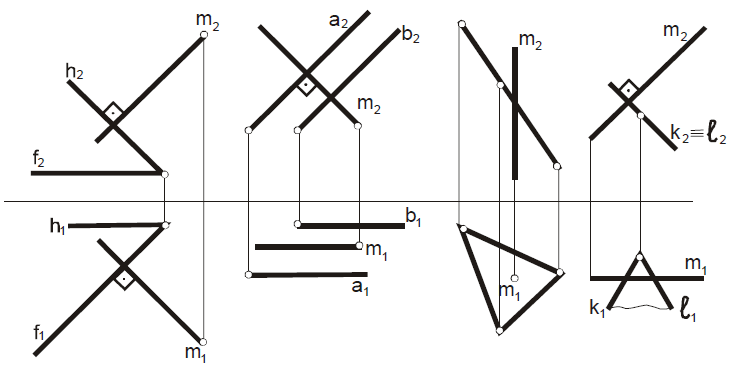
Определить, перпендикулярна ли прямая m плоскости
Задача 24
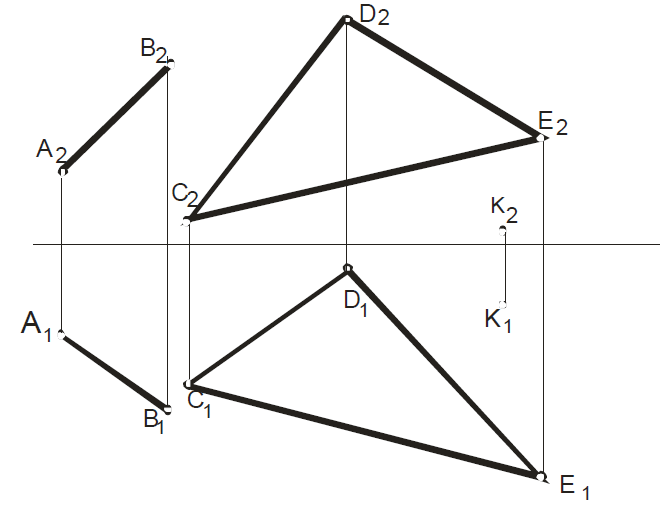
Через точку К провести перпендикуляр к плоскости CDE. Через прямую АВ провести плоскость, параллельную плоскости CDE.
Тема 4. ПОЗИЦИОННЫЕ ЗАДАЧИ
4.1 ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ
Вопросы для подготовки
1. Какие задачи относятся к позиционным?
2. Какой способ применяют для решения позиционных задач?
3. Из каких этапов (алгоритм ) состоит решение задачи по определению точки пересечения прямой с плоскостью общего положения?
4. Упрощается ли решение задачи, если плоскость проецирующая? Если прямая проецирующая?
5. Как определяется видимость прямой.
Задача 25
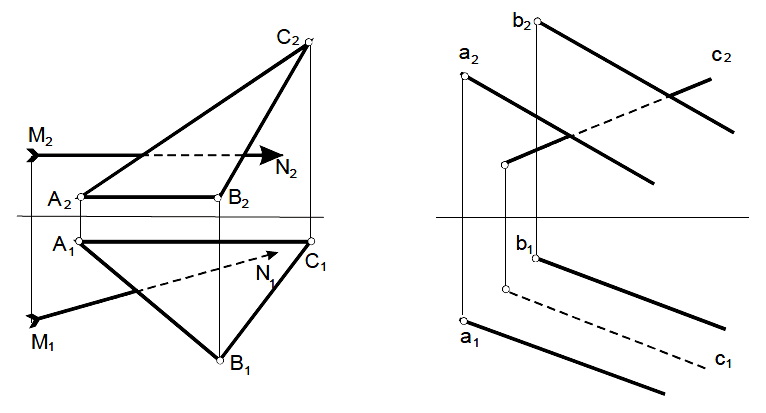
|
Построить точку пересечения прямой MN с плоскостью АВС. Определить видимость прямой. |
|
Построить точку пересечения прямой с с плоскостью β(а b). Определить видимость прямой. |
Задача 26
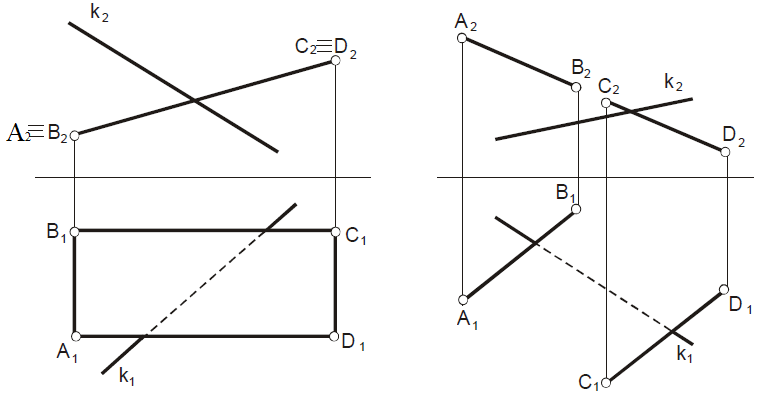
Построить точку пересечения прямой k с плоскостью ABCD.
Определить видимость прямой.
Задача 27
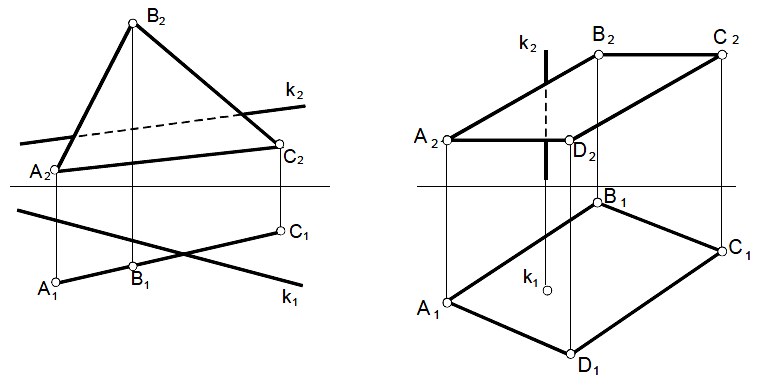
|
Построить точку пересечения прямой k с плоскостью ABC. Определить видимость прямой |
|
Построить точку пересечения прямой k с плоскостью ABCD. Определить видимость прямой |
4.2 ПЕРЕСЕЧЕНИЕ ДВУХ ПЛОСКОСТЕЙ
Задача 28
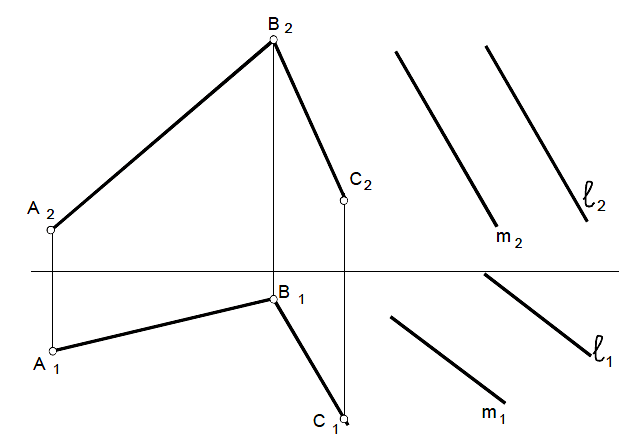
Построить линию пересечения двух плоскостей α (АВ∩ВС) и β (ℓ II m)
Задача 29
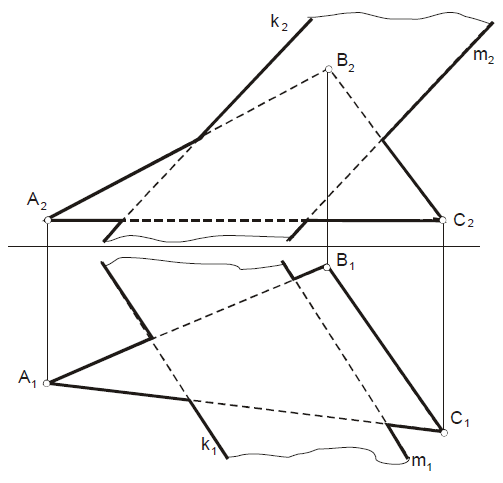
Построить линию пересечения двух плоскостей α (ΔАВС) и β (k| |m). Определить видимость.
Задача 30
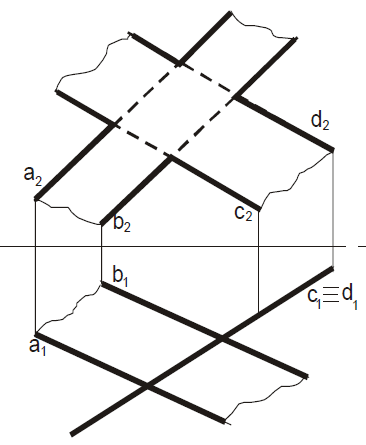
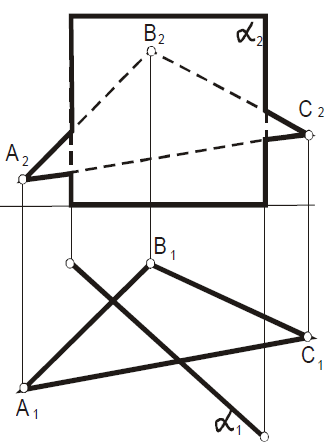
|
Построить линию пересечения плоскостей α и β(ABC). Определить видимость. |
Построить линию пересечения плоскостей α(a| |b) и β(c| |d). Определить видимость. |
Задача 31
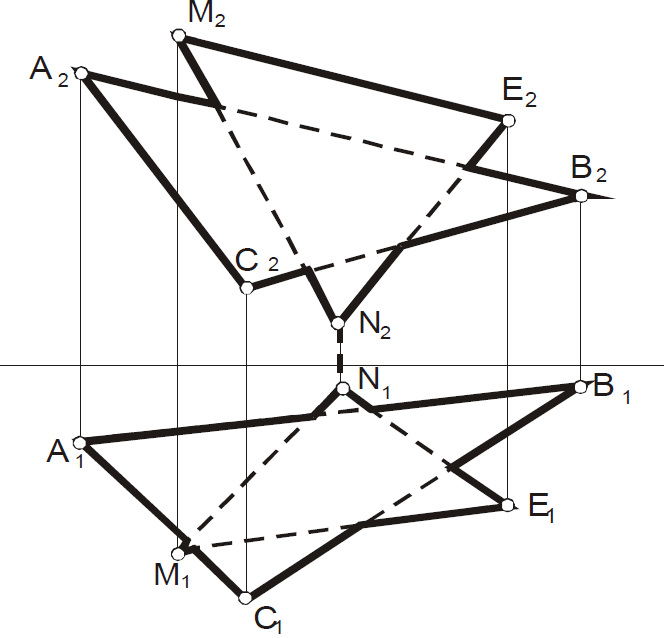
Построить линию пересечения двух плоскостей α(ABC) и β(MNE). Определить видимость.
Тема 5. ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА
5.1 Способ замены плоскостей проекций
Вопросы для подготовки
1. Перечислите основные способы преобразования комплексного чертежа.
2. С какой целью применяют преобразование комплексного чертежа?
3. В чем состоит сущность способа замены плоскостей проекций?
4. Чем следует руководствоваться при выборе положения новой плоскости проекций?
5. Что обозначают символы: Х12; Х14; Х45
6. Как построить новую проекцию точки при способе замены плоскостей проекций?
7. Достаточно ли одной замены для решения всех типов задач?
8. Какие операции необходимо выполнить, чтобы найти натуральную величину плоскости общего положения?
Задача 32 Задача 33
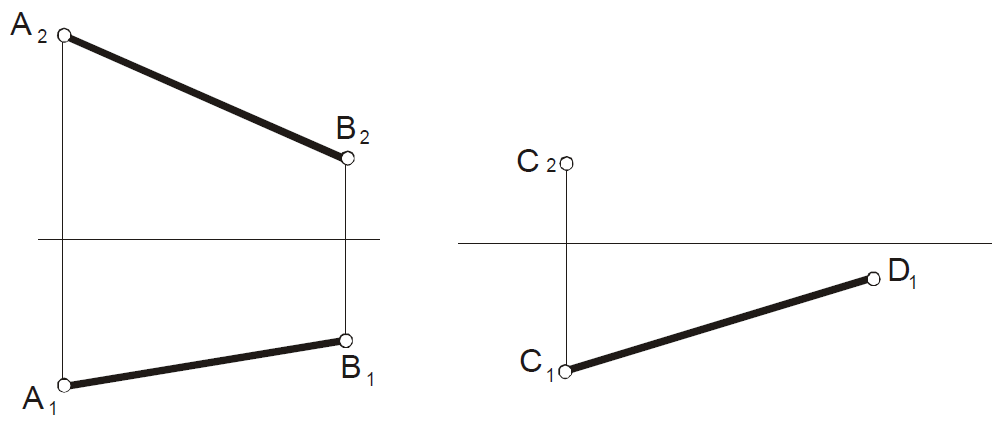
|
Определите истинную величину отрезка АВ и углы наклона его к плоскости проекций П1 и П2 |
Построить фронтальную проекцию точки D, если длина отрезка CD равна 70 мм |
Задача 34
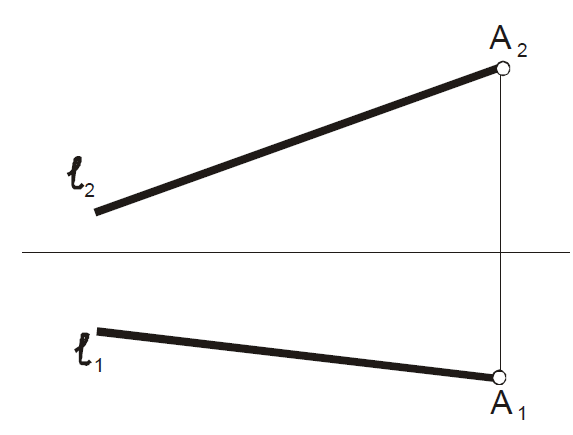
На прямой ℓ отложить от точки А отрезок АВ равный 35 мм
Задача 35
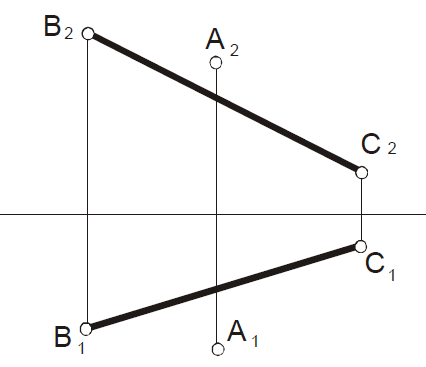
Найти
расстояние от точки А
до прямой ВС
Задача 36
П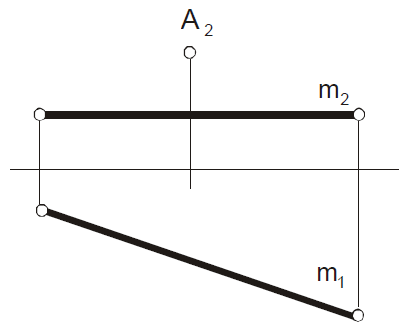 остроить
горизонтальную проекцию точки А,
если она
остроить
горизонтальную проекцию точки А,
если она
отстоит от прямой m на 15 мм.
З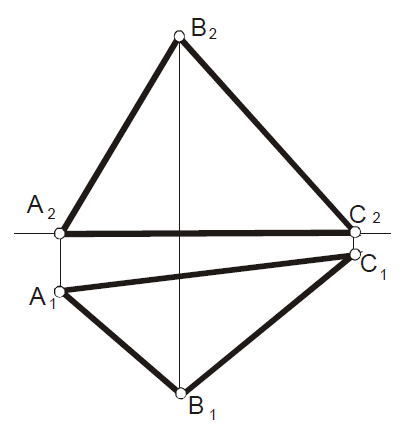 адача
37
адача
37
Определить угол наклона
треугольника АВС к
плоскости
П1
Задача 38
Определить расстояние между
д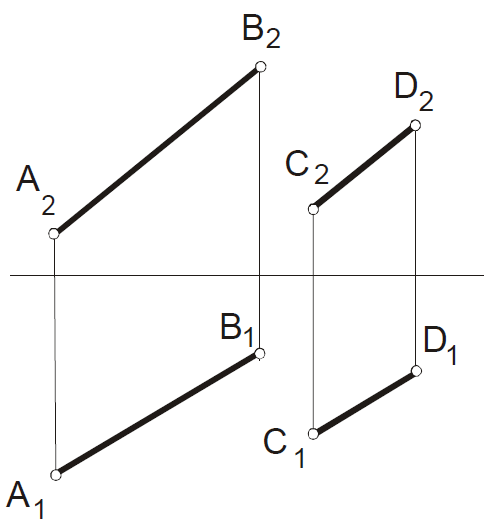 вумя
параллельными прямыми
вумя
параллельными прямыми
З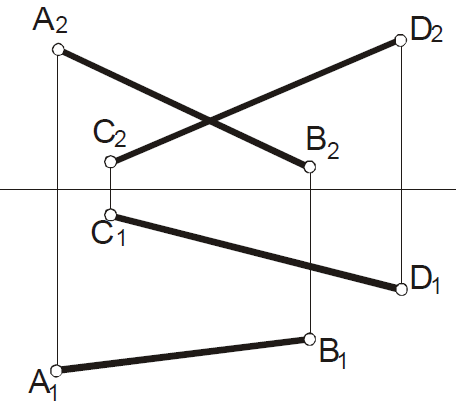 адача
39
адача
39
Определить расстояние между
скрещивающимися
прямыми
Задача 40
О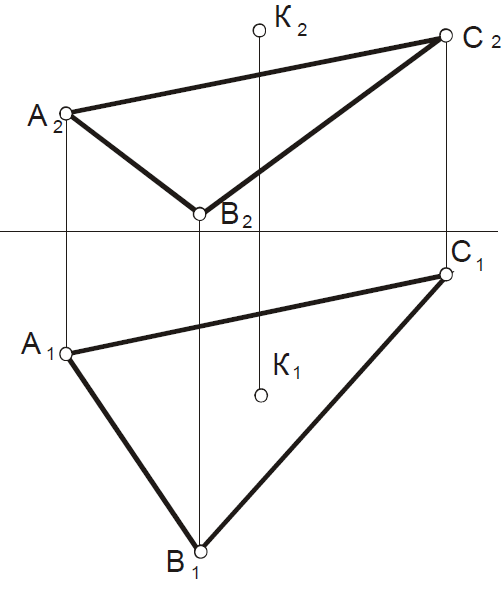 пределить
расстояние
пределить
расстояние
от точки К до плоскости ΔАВС
Задача 41
О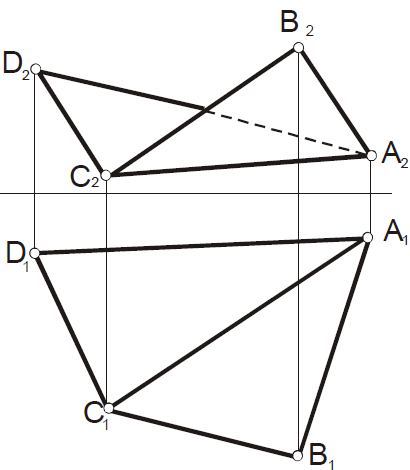 пределить
величину двугранного угла между двумя
плоскостями АВС
и CDA.
пределить
величину двугранного угла между двумя
плоскостями АВС
и CDA.
Тема 6. ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА
6.2 Способ вращения вокруг проецирующей прямой
Вопросы для подготовки
1. В чем состоит суть способа вращения?
2. Как расположена ось, относительно которой производят вращение?
3. Как изображается на плоскостях проекций траектория точки, при ее вращении вокруг оси ?
4. Как необходимо вращать плоскость общего положения, чтобы преобразовать ее в проецирующую?
5. Как необходимо вращать прямую общего положения, чтобы преобразовать ее в проецирующую?
6. Какие действия необходимо произвести для определения натуральной величины прямой или плоскости?
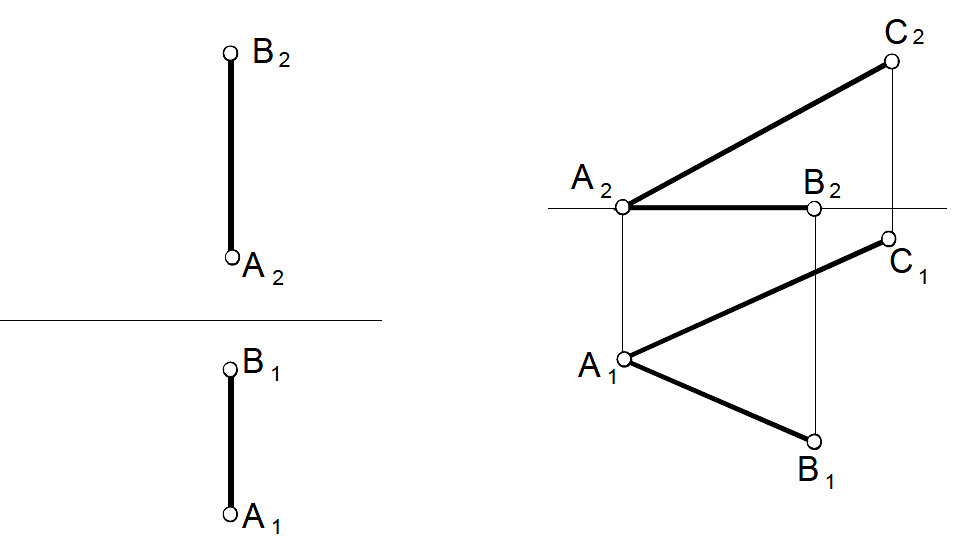
Задача 42 Задача 43
|
Оделить натуральную величину отрезка АВ и углы его наклона к плоскостям П1 и П2. |
Плоскость общего положения угла ВАС преобразовать в проецирующую. |
6.3 Плоскопараллельное перемещение
Вопросы для подготовки
1. В чем состоит сущность способа замены плоскостей проекций?
2. С какой целью применяют плоскопараллельное перемещение?
3. Каким правилом следует руководствоваться при выполнении плоскопараллельного перемещения?
4. Есть ли какая то связь между методом плоскопараллельного перемещения и методом замены плоскостей?
5. В чем достоинство этого метода?
6. Какие действия необходимо выполнить, чтобы найти натуральную величину прямой общего положения?
Задача 44
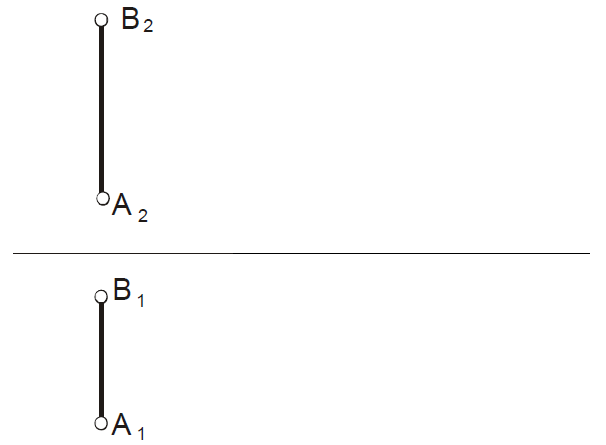
Преобразовать прямую уровня в горизонтально проецирующую.
Задача 45
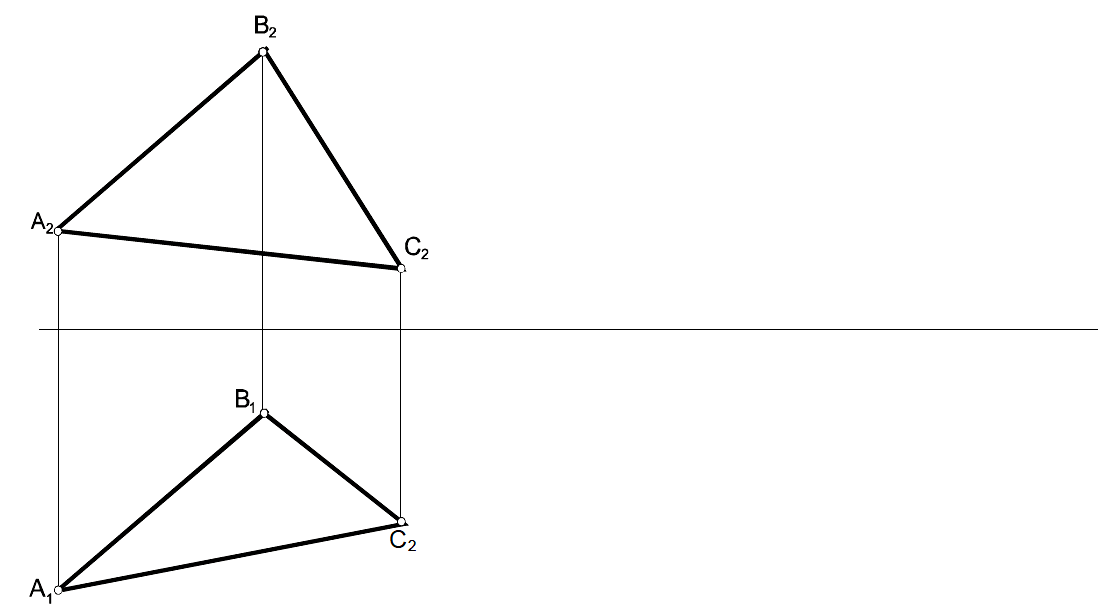
Определить натуральную величину плоскости ΔАВС.
Задача 46
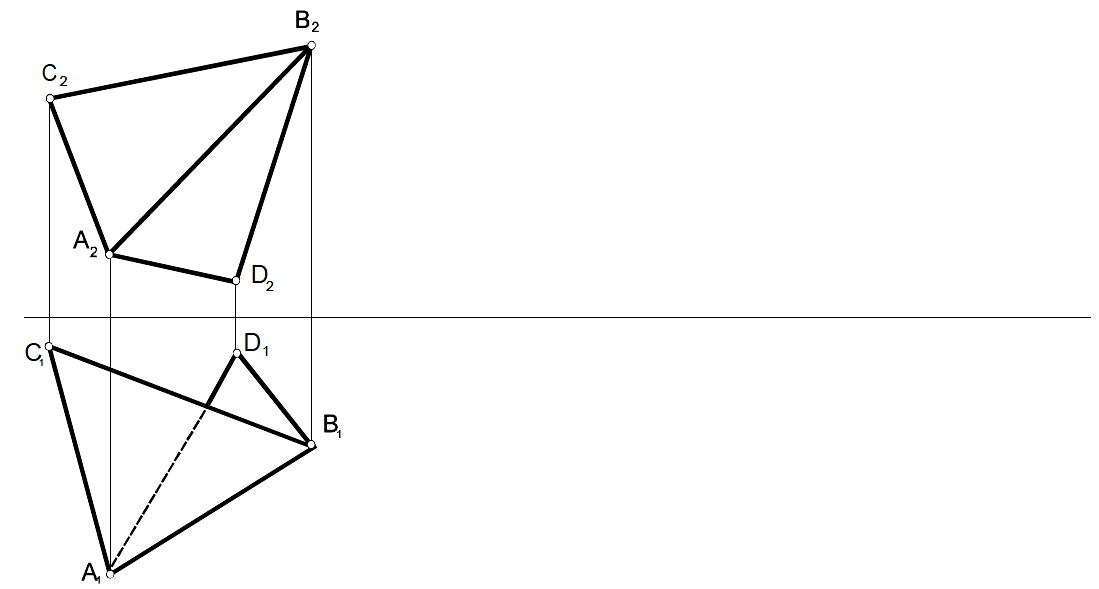
Используя способ плоскопараллельного перемещения определить натуральную величину двугранного угла.
ТЕМА 8. ПОВЕРХНОСТИ
Вопросы для подготовки
1. Перечислите виды поверхностей, которые вы знаете.
2. Какие элементы участвуют в образовании этих поверхностей?
3. Что такое определитель поверхности? Какие элементы составляют определитель поверхности?
4. Чем очерк отличается от каркаса?
5. Как найти недостающую проекцию точки, лежащую на линейчатой поверхности?
6. Перечислите главные линии поверхности вращения
7. Как найти недостающую проекцию точки, лежащей на поверхности вращения?
Задача 47
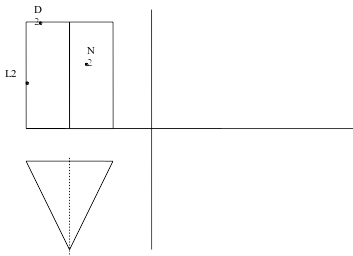
Начертить третью проекцию призмы.
Задача 48
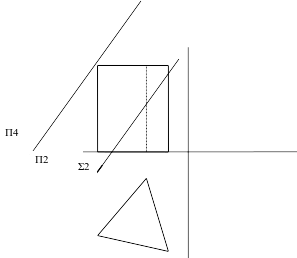
Начертить третью проекцию призмы.
Определить натуральную величину сечения.
Задача 49
а) б)
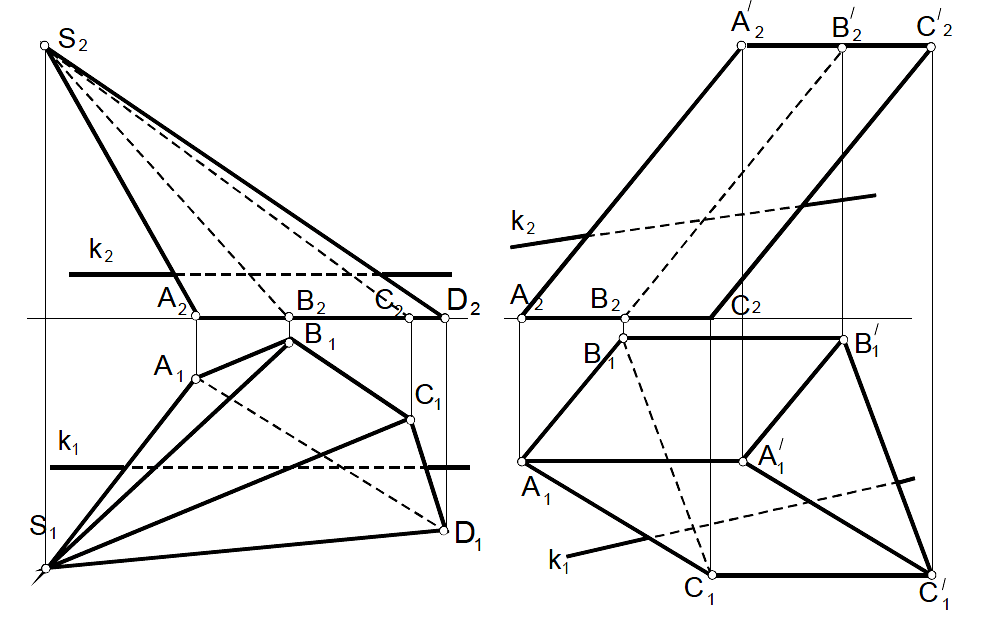
|
Найти точки пересечения прямой k с поверхностью пирамиды. Показать видимость. |
Найти точки пересечения прямой k с поверхностью призмы. Показать видимость |
Задача 50
а) б)
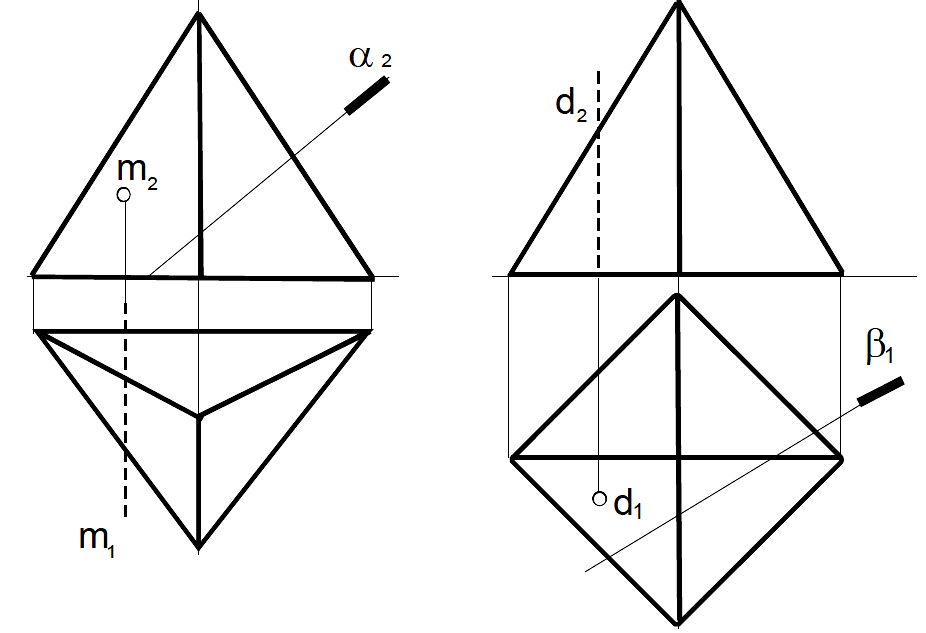
Построить точку пересечения прямой и плоскости с пирамидой. Определить видимость прямой.
Задача 51
а) б)
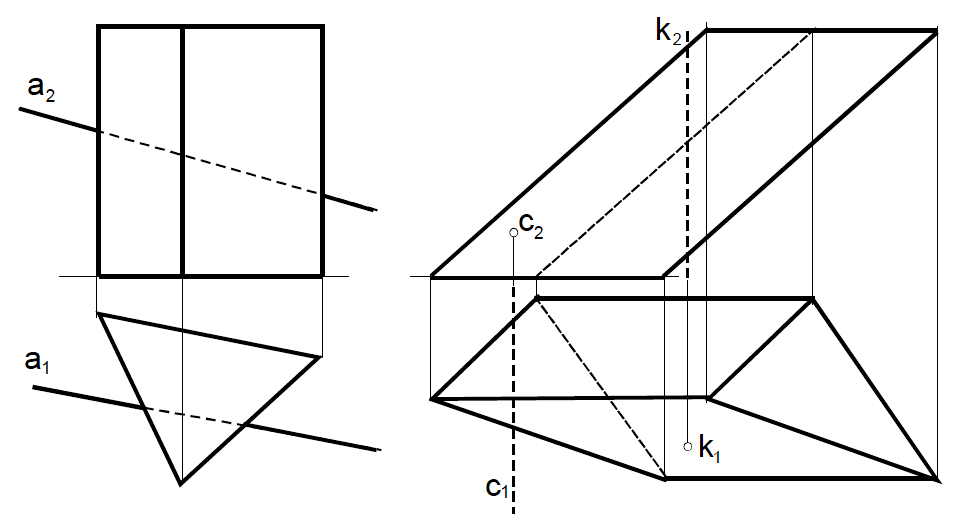
Построить точку пересечения прямой с призмой. Определить видимость прямой.
Задача 52
а) б)
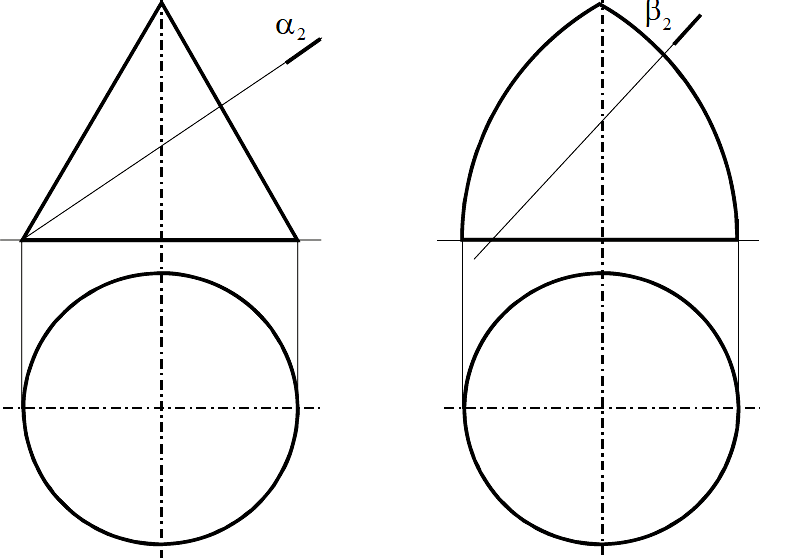
Построить линию пересечения плоскости с поверхностью
Задача 53
а) б)
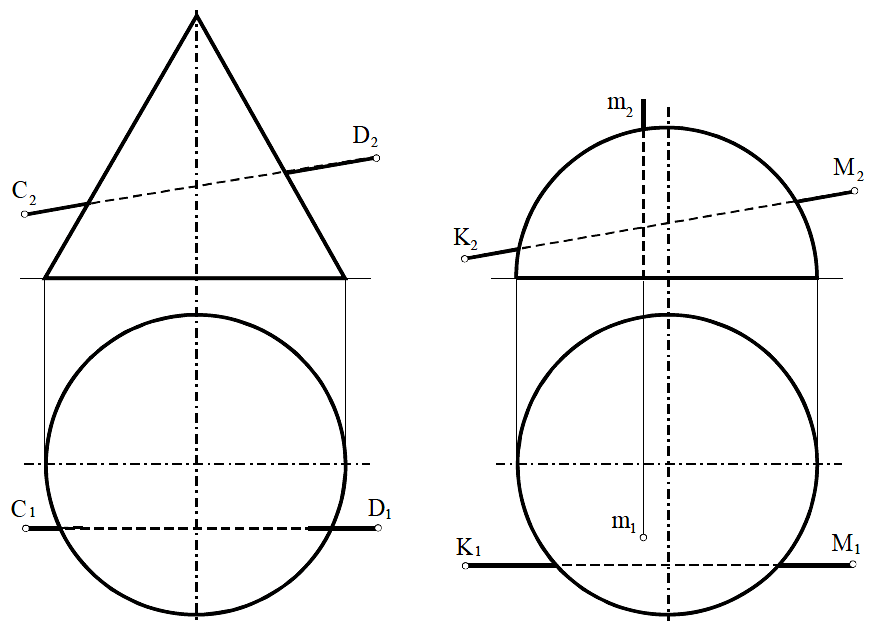
Построить линию пересечения прямой с поверхностью вращения. Показать видимость.
Задача 54
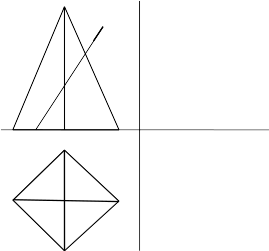
Начертить третью проекцию пирамиды c сечением.
Порядок выполнения
1. Построить третью (профильную) проекцию пирамиды.
2.На фронтальной проекции по линии сечения поставим и обозначим точки на боковых ребрах (12, 22 и т. д.).
3. Перенесите проекции точек на горизонтальную проекцию на одноименные ребра (11, 21 и т. д.) и соединить их прямыми линиями.
4. Перенести точки на профильную проекцию призмы.
5. Обвести на профильной проекции сечение по точкам тонкими прямыми линиями. Определяем видимость линии сечения на профильной проекции и окончательно обводим с учетом видимости толстой основной и штриховой линиями.
Задача 55
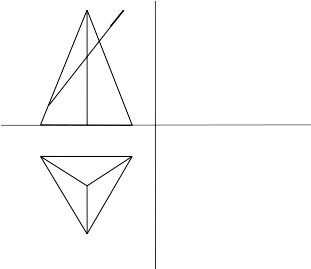
Начертить третью проекцию пирамиды с сечением и построить развертку с нанесенными линиями сечения.
Задача 56
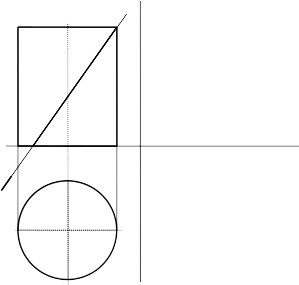
Начертить третью проекцию цилиндра c сечением.
Порядок выполнения
1. Построить третью (профильную) проекцию цилиндра.
2.На фронтальной проекции по линии сечения поставим и обозначим точки (12, 22 и т. д.).
3. Перенесите проекции точек на горизонтальную проекцию (11, 21 и т. д.)
4. Перенести точки на профильную проекцию цилиндра.
5. Обвести на профильной проекции сечение по точкам тонкой плавной линией. Учитываем, что наклонный срез цилиндра – овал.
6. Определяем видимость линии сечения на профильной проекции и окончательно обводим с учетом видимости толстой основной и штриховой линиями.
Задача 57
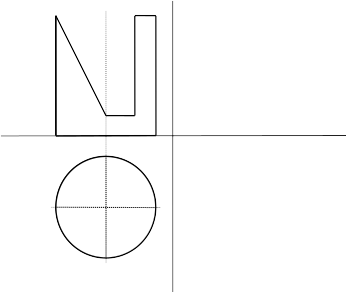
Начертить третью проекцию цилиндра с вырезом и построить развертку боковой поверхности.
Задача 58
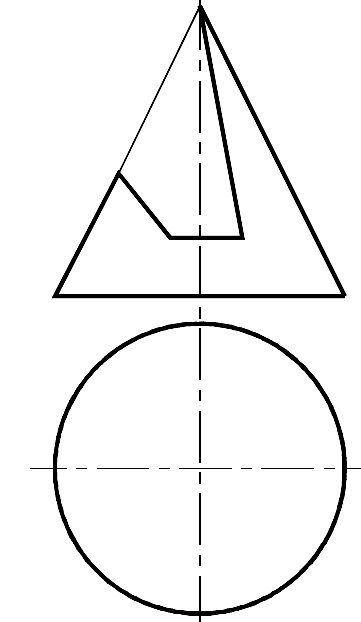
Построить три проекции конуса с вырезом
Задача 59
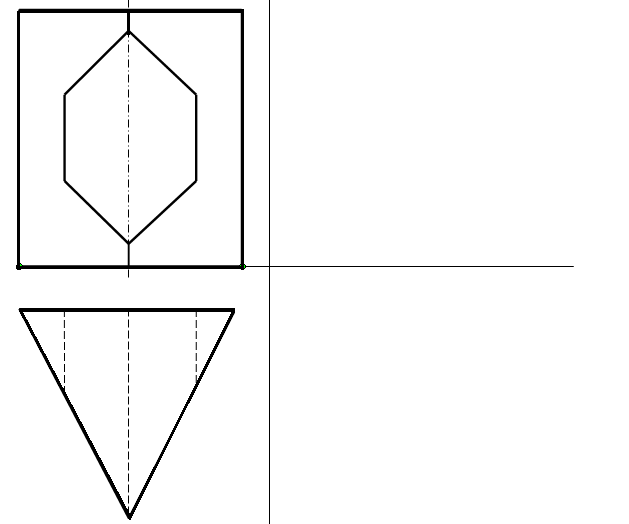
Построить третью проекцию призмы с вырезом.
Задача 60
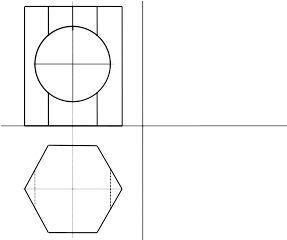
Начертить третью проекцию призмы с вырезом и построить развертку боковой поверхности.
Задача 61
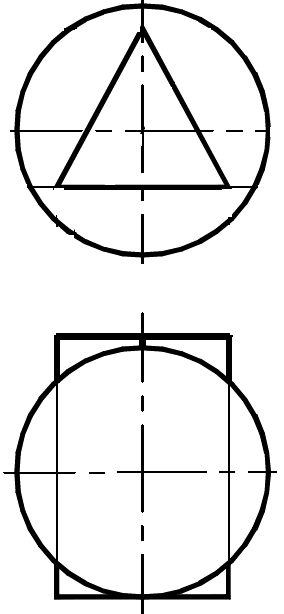
Построить три проекции линии пересечения сферы и призмы
Задача 62
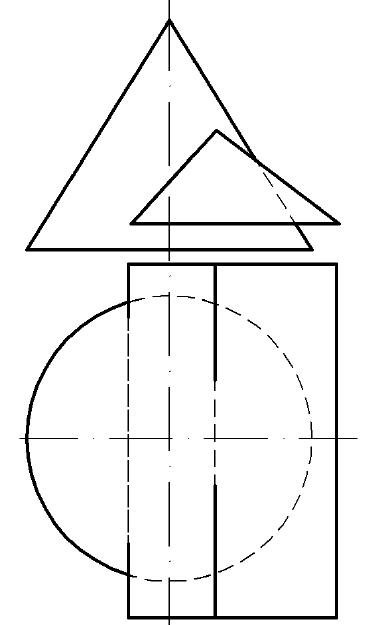
Построить три проекции линии пересечения конуса и призмы.