ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.12.2020
Просмотров: 133
Скачиваний: 3
Практическая
работа
№
4
Усреднение
данных
Задание
№
1.
Помехозащищенные
алгоритмы
сглаживания
Из
рассмотренных
алгоритмов
помехозащищенными
являются
алгоритмы
скользящего
медианного
среднего
(
СМС
)
и
релейно
-
экспоненциального
сред
-
него
(
РЭС
).
1.
Исходный
ряд
данных
проверьте
на
наличие
выбросов
,
если
таковые
имеются
,
эти
отсчеты
следует
исключить
из
рассмотрения
.
2.
После
исключения
отсчетов
предположительно
являющихся
выброса
-
ми
произвести
расчет
настроечного
параметра
β
алгоритма
скользяще
-
го
релейно
-
экспоненциального
среднего
(
РЭС
).
Параметр
α
задать
равным
0,3.
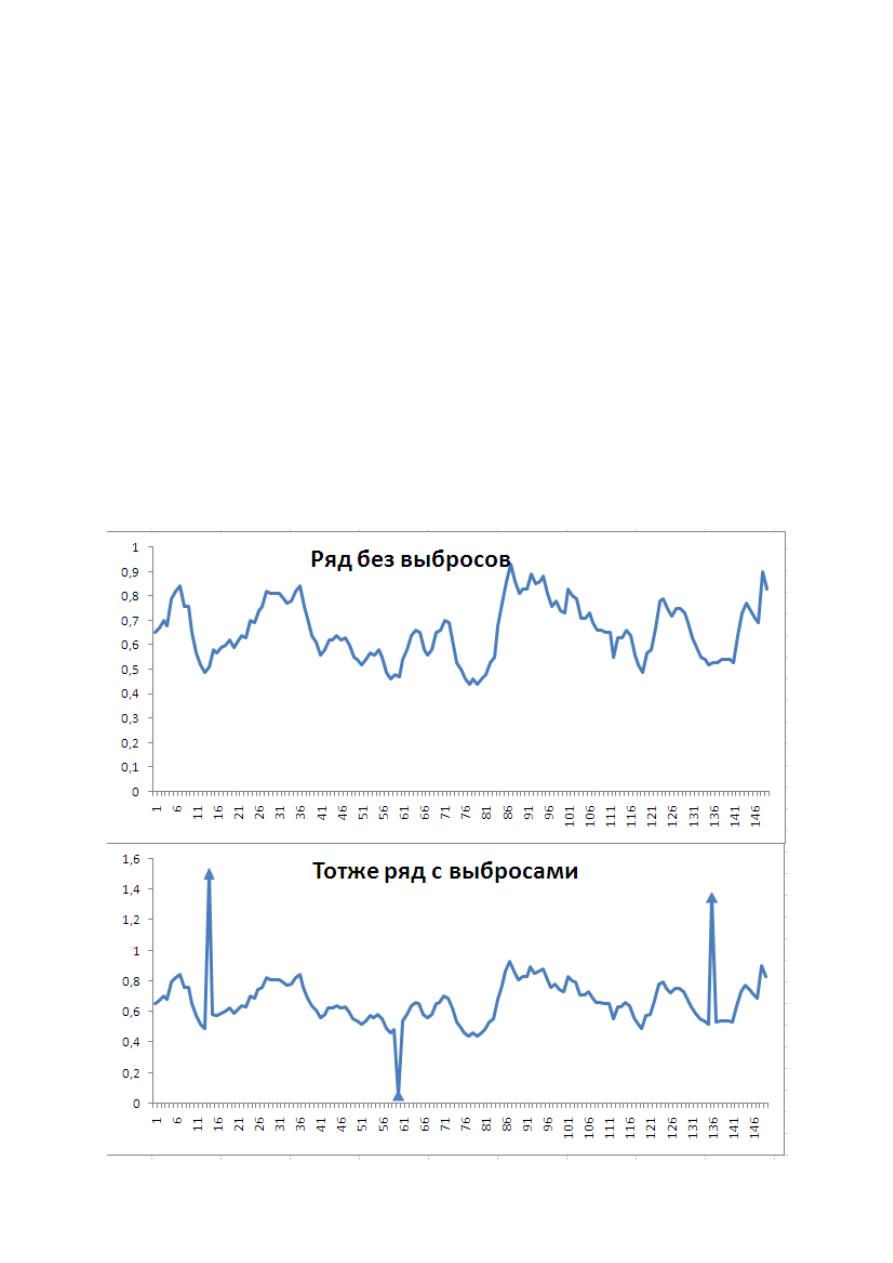
3.
Скопировать
исходный
ряд
в
новый
столбец
и
искусственно
внести
в
него
выбросы
–
сделать
некоторые
значения
ряда
данных
существенно
больше
всех
остальный
4.
Ряд
с
выбросами
сгладить
с
использованием
алгоритмов
РЭС
с
рассчи
-
танным
значением
настроечного
параметра
β
и
α
=0,3,
СМС
с
окном
скольжения
эквивалентным
α
и
СЭС
с
α
=0,3.
5.
Вывести
графики
исходного
ряда
и
сглаженных
рядов
в
одних
осях
.
Сравнить
их
между
собой
.
Чем
они
отличаются
и
почему
?
Задание
№
2
.
Выбор
наилучшего
настроечного
параметра
сглаживающе
-
го
алгоритма
с
помощью
двухкомпонентного
критерия
качества
сглаживания
и
воспроизводимости
оценок
.
При
выборе
настроечного
параметра
алгоритма
сглаживания
необходимо
учесть
следующие
требования
:
сглаженный
ряд
должен
обладать
высокой
сте
-
пенью
гладкости
по
сравнению
с
исходным
,
а
также
должен
отражать
свойства
исходного
динамического
сигнала
.
Исходя
из
этого
,
двухкомпонентный
крите
-
рий
К
должен
содержать
гладкостную
и
точностную
составляющие
.
1
отн.
,
max
отн.
отн.
отн.
отню
;
b
1
+
b
2
=1
где
отн.
,
отн.
–
нормированные
значения
показателей
гладкости
и
точ
-
ности
;
b
1
,
b
2
–
весовые
коэффициенты
.
Порядок
выполнения
задания
1
1.
На
диске
W:\
Анализ
данных
откройте
файл
«2-
х
компонентный
критерий
».
2.
В
столбец
В
«
Исходный
ряд
»
внести
значения
своего
ряда
.
3.
В
столбце
С
«
Экспоненциально
сглаженный
ряд
»
произвести
сглажива
-
ние
исходного
ряда
с
использованием
алгоритма
скользящего
экспонен
-
циального
среднего
,
задав
значение
α
=0,1
в
ячейке
А
3:
ℓ
ℓ
1
ℓ
ℓ
1
,
где
α
–
настроечный
параметр
α
0, 1];
ℓ
–
сглаженное
значение
на
ℓ
-
ый
момент
времени
;
x
(
ℓ
) –
фактическое
значение
ряда
данных
на
ℓ
-
ый
момент
времени
4.
Расчет
гладкостной
и
точностной
составляющих
,
а
также
значения
двух
-
компонентного
критерия
с
использованием
различных
алгоритмов
сверт
-
ки
производится
автоматически
:
отн.
отн.
отню
;
2
2
2
1
1
)
(
отн
отн
II
Q
b
Q
b
Q
⋅
+
⋅
=
,
3
2
2
1
1
)
(
отн
отн
III
Q
b
Q
b
Q
⋅
+
⋅
=
,
отн
отн
IV
Q
b
Q
b
Q
2
2
1
1
⋅
+
⋅
=
,
отн
отн
V
Q
b
Q
b
Q
2
2
3
1
1
⋅
+
⋅
=
,
отн
отн
VI
Q
b
Q
b
Q
2
2
4
1
1
⋅
+
⋅
=
,
Полученные
значения
двухкомпонентного
критерия
,
рассчитанные
по
раз
-
личным
формулам
свертки
,
заносятся
в
ячейки
M3:S3
5.
Скопировать
содержимое
ячеек
M3:S3
и
вставить
с
таблицу
скопирован
-
ные
значения
.
Для
этого
выделить
ячейку
столбца
альфа
,
соответствую
-
щую
используемому
на
текущем
шаге
значению
α
,
нажать
правую
кнопку
мыши
и
в
появившемся
меню
выбрать
команду
Специальная
вставка
.
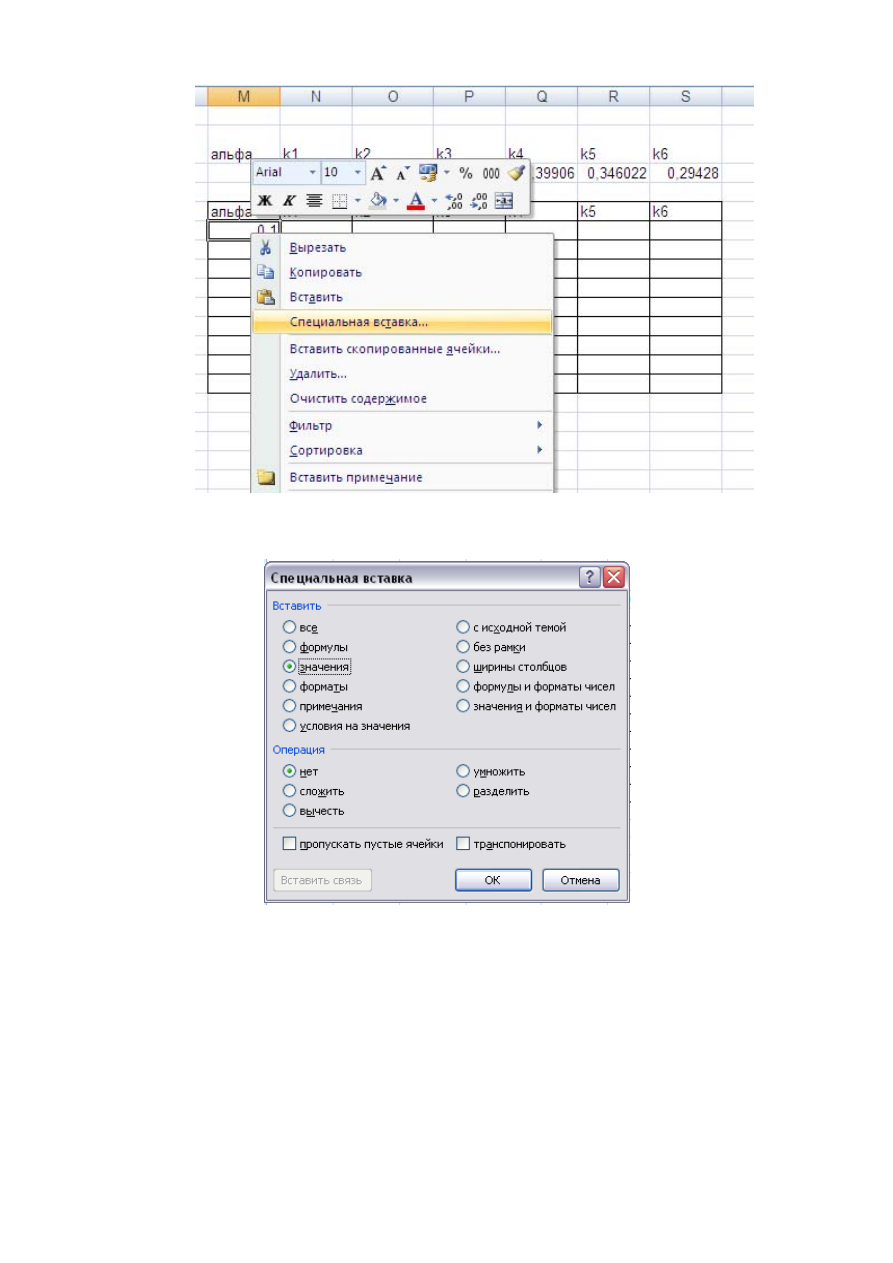
В
диалоговом
окне
Специальная
вставка
установить
индикатор
в
строке
Значе
-
ния
.
6.
Далее
в
ячейке
А
3
изменять
значения
α
с
шагом
0,1,
придав
ему
последо
-
вательно
значения
0,2, 0,3, …., 0,9.
7.
Заполнив
таблицу
,
будет
построен
график
зависимости
значений
2-
х
ком
-
понентного
критерия
,
рассчитанного
с
использованием
различных
фор
-
мул
свертки
,
от
значений
настроечного
параметра
алгоритма
скользящего
экспоненциального
среднего
α
.
8.
Среди
графиков
выбрать
те
,
на
которых
имеется
ярко
выраженный
экс
-
тремум
максимум
.
Значение
настроечного
параметра
α
,
при
котором
гра
-
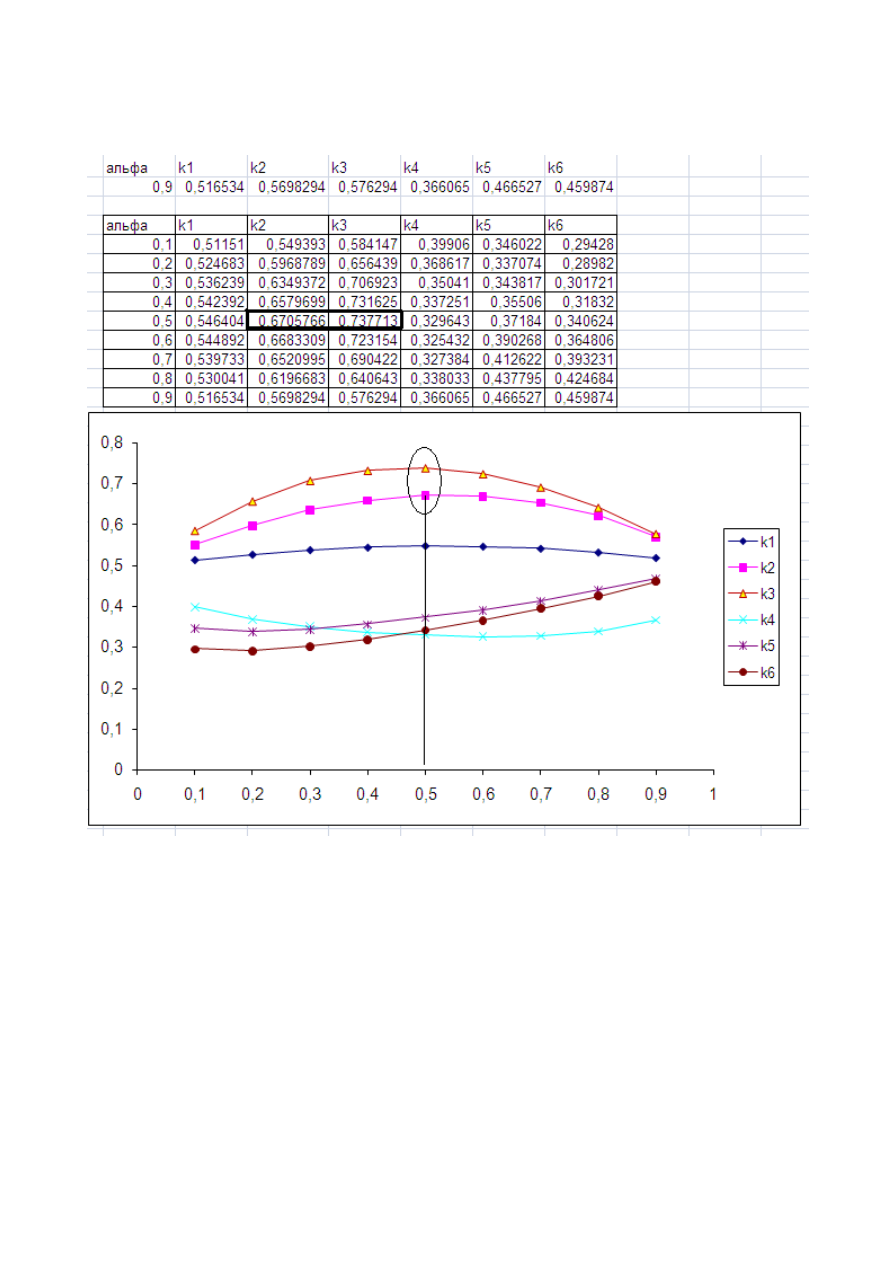
фики
достигают
максимального
значения
,
и
есть
наилучшее
.
В
приведен
-
ном
примере
это
значение
0,5
9.
Далее
повторить
расчеты
критерия
,
изменяя
α
с
шагом
0,01,
в
большую
или
в
меньшую
сторону
в
зависимости
от
того
,
в
каком
направлении
из
-
менения
α
значение
критерия
увеличивается
,
начиная
с
выбранного
наи
-
лучшего
значения
п
. 8.
10.
По
полученной
таблице
выбирается
наилучший
α
,
аналогично
п
. 8.
В
приведенном
примере
в
качестве
наилучшего
α
можно
взять
значения
0,52
или
0,53