ЦВМ (компьютер, алгоритм, цифровой регулятор, цифровое управляющее устройство) преобразует цифровой сигнал у(ti)другой цифровой сигнал u(ti) в соответствии с выбранным законом управления, т.е. по некоторому алгоритму. Для целей анализа удобно в качестве математической модели сигнала u(ti) принять числовую последовательность, которую называют управляющей последовательностью. Итак, ЦВМ будем интерпретировать как устройство, преобразующее одну числовую последовательность у(ti)в другую последовательность u(ti),т. е. как дискретный фильтр.

ЦАП преобразует управляющую последовательность u(ti)в непрерывный управляющий сигнал u(t). Такое преобразование необходимо, так как большинство объектов управления представляют собой аналоговые устройства. Заметим, что в промежутки между моментами дискретизации, т.е. при , i = 0, 1, 2,… система работает как разомкнутая, т.е. сигнал по цепи обратной связи не поступает.

Также необходимо упомянуть, что информация о желаемом законе изменения управляемой величины введена в память ЦВМ и используется при выработке управляющей последовательности.

В настоящее время в основном применяются ЦСАУ с периодической дискретизацией, т.е. системы, в которых дискретизация осуществляется в моменты дискретизации t=iT , i = 0, 1, 2,…. В этом случае моменты дискретизации отстоят друг от друга на период дискретизации T. Только такие системы и будут представлять предмет нашего рассмотрения. Для упрощения записи используем другие обозначения последовательностей y(ti)и u(ti), a именно:

где i - дискретный аргумент. Следовательно, y[i] и u[i] представляют собой функции дискретного аргумента, называемые также решетчатыми функциями.

Особенностью применения ЦВМ в ЦСАУ является то, что они должны работать в реальном масштабе времени, т.е. время обработки сигнала y(t), осуществляемое АЦП,

ЦВМ и ЦАП, не должно превышать периода дискретизации Т. Это обстоятельство повышает требования к быстродействию используемых в системах ЦВМ.

Для синхронизации работы всех цифровых элементов ЦСАУ служит таймер реального времени, обеспечивающий последовательное функционирование АЦП, ЦВМ и ЦАП

10. Дискретный фильтр и его описание.

ЦСАУ содержат как непрерывные, так и дискретные сигналы, что затрудняет описание системы в целом. Однако, если ограничиться описанием системы в моменты дискретизации t = iT , то указанного затруднения можно избежать. В этом случае, заменяя последовательное соединение ЦАП, ОУ и АЦП в предыдущей Дискретным фильтром (Д - фильтром) называют устройство, на входе и выходе которого имеют место числовые последовательности (рис).

---

Обозначим через u[i] входную, а через y[i] выходную последовательности дискретного фильтра, которую также называют реакцией дискретного фильтра на входной сигнал u[i]. Ограничимся рассмотрением линейных стационарных фильтров. При этом математическую модель Д - фильтра можно представить в виде линейного разностного уравнения с постоянными коэффициентами (ЛРУ):

соответственно последовательности выхода и входа, смещенные в сторону опережения

на к периодов дискретизации, а

- постоянные коэффициенты. Если

то n определяет порядок разностного уравнения, а следовательно, и порядок Д - фильтра. Условие физической осуществимости Д - фильтра записывается в виде

Если оно не выполняется, то для вычисления выходной последовательности y[i] требуются будущие значения входной последовательности u[i+1], u[i+2]…, которые к моменту времени еще не поступили на вход дискретного фильтра.

Так, пусть

Тогда следует, что

Это уравнение идеального экстраполятора -

устройства, предсказывающего в момент будущее значение

входной последовательности отстоящее от настоящего момента времени на один период дискретизации. Разумеется, такой экстраполятор нельзя реализовать.

11. Прямое решение линейных разностных уравнений.

Линейное разностное уравнение описывает связь выхода и входа Д-фильтра лишь в неявной форме. Чтобы найти его реакцию на некоторую входную последовательность, надо это уравнение решить. Здесь, как и для непрерывных систем, знание поведения входной последовательности u[i] для i = 0,1,2, ... и равенство ее нулю при i < 0 позволяют получить лишь частичное описание выходной последовательности y[i] при i = 0,1,2. Для системы порядка n необходимо иметь n дополнительных данных, соответствующих начальным условиям в непрерывном случае. Однако в отличие от ситуации с дифференциальными уравнениями определение реакции Д-фильтра оказывается более простым делом. Покажем это, выразив уравнение (1) через последовательности, смещенные в сторону запаздывания. Заменяя в

на i, т.е. полагая а затем, обозначая как i , получаем другую форму записи разностного уравнения Д-фильтра

представляют собой соответственно последовательности выхода и входа, смещенные в сторону запаздывания на k периодов дискретизации.

Полагая , из (2) получаем рекуррентное соотношение

---

позволяющее определять выходную последовательность y[i], другими словами, реакцию Д-фильтра на входную последовательность u[i]. Отметим, что для уравнения (3) начальными условиями являются значения y[-1], y[-2],…,y[-n], которые будем считать заданными. За начальный момент времени принимаем i=0. Если хотя бы одно из значений y[-1] , y[-2] ,…, y[-n] не равно нулю, то говорят, что Д-фильтр предварительно возбужден. Если y[-1]=y[-2]=…=y[-n]=0, то говорят, что Д-фильтр предварительно невозбужден

12. 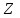- преобразование и его свойства.


причём р=c + jω, а T-период дискретизации. Z-преобразование существует, если |z]> z0, где z0, - радиус абсолютной сходимости.

Найдём Z - преобразование единичной последовательности x[i] = 1[i]:

1. Теорема линейности.

Z-преобразование линейной комбинации двух последовательностей:

где|a,b = const, x₁*(z) = Z{x₁[i]}, x₂*(z) = Z{x₂[i]}

2. Теорема смещения (сдвига).

Целое k > 0.

a) Смещение в сторону запаздывания на k периодов дискретизации:

б) Смещение последовательности в сторону опережения на k период дискретизации:

Если x[-1]= x[-2]=…= x[=k]=0, то

Если x[0] = x[1] =…= x[k - 1] = 0, тогда

Если x[0] = x[1] =…= x[k - 1] = 0, тогда

3. Теорема о конечном значении.

lim x[i] = lim (z - 1)x (z),

если (z - 1)х (z) не имеет полюсов на или вне окружности единичного радиуса

комплексной плоскости z.

4. Теорема свёртки.

13. Передаточная функция дискретного фильтра.

Определяя Z - преобразование от левой и правой частей ЛРУ

с учётом теоремы смещения, получаем уравнение Д - фильтра в изображениях

Здесь

- Z- преобразование входной последовательности, а М (z) - многочлен, учитывающий начальные условия y[0],y[1],…y[n - 1].

Последнее уравнение можно представить в виде алгебраического уравнения

D'(z)y' (z) = K' (z)u' (z) + M' (z),

поделив обе части которого на D'(z), найдём Z- преобразование выходной последовательности

Если фильтр предварительно не возбуждён, то М (z) = 0 и, следовательно

называется передаточной функцией дискретного фильтра.

Определение. Передаточной функцией Д - фильтра называется отношение Z- преобразований выходной и входной последовательностей предварительно невозбуждённого Д - фильтра, т.е.

---

14. Передаточная функция объекта, управляемого от ЦВМ.

Из файла

15. Структуры систем цифрового и непрерывного управления.

Из файла

16. Структурная схема цифровой системы с прямой и обратной связью.

17. Структурная схема ЦСАУ с единичной обратной связью.

18. Передаточные функции цифровой системы управления с обратной связью.

19. Уравнение цифровой системы с обратной связью.

20. Анализ устойчивости цифровых систем по начальным условиям.

21. Понятие о 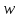- преобразовании.

22. Анализ точности ЦСАУ в установившемся режиме.

23. Определение установившейся ошибки ЦСАУ для полиномиальных входных сигналов.

24. Анализ качества переходных процессов. Определение переходной последовательности на основе теоремы разложения - преобразования.

25. Определение переходной последовательности на основе разложения 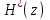в ряд Лорана, и по методу, базирующемуся на разностном уравнении системы.

26. Выбор периода дискретизации. Теорема Котельникова.

27. Выбор периода дискретизации из условия близости свойств цифровой системы и её непрерывного прототипа в установившемся режиме.

28. Выбор периода дискретизации из условия близости свойств цифровой системы и её непрерывного прототипа в переходном режиме.

---

Смотрите также файлы

• Практическое задание 2 Никулиной Елены Владимировны Заполните таблицу История развития психологии.doc

• Активная и пассивная макроэкономическая политика Определение понятий.pptx

• Курсы повышения квалификации по программе Актуальные вопросы акушерской и гинекологической помощи в объёме 144 ч г. Москва.docx

• Нэп экономическая политика Советской России, сменившая политику военного коммунизма.docx

• Решение Товарищества.docx