Файл: Численное интегрирование Метод прямоугольников (метод прямоугольных сумм).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 36
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Численное дифференцирование
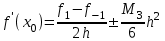 (14)
(14)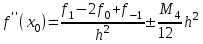 (15)
(15)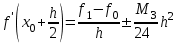 (16)
(16)Соотношения (11) и (13) соответственно дают
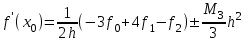 (17)
(17)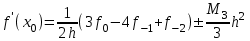
Численное интегрирование
Метод прямоугольников (метод прямоугольных сумм):
Пример 1: с помощью формул левых и правых прямоугольников вычислить
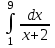 , полагая n = 4.
, полагая n = 4.Зная приделы интегрирования a = 1 и b = 9, находим шаг
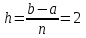 ; тогда точками разбиения служат
; тогда точками разбиения служат 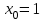 ,
, 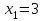 ,
, 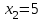 ,
, 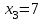 ,
, 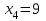 , а значения подынтегральной функции
, а значения подынтегральной функции 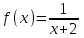 в этих точках таковы:
в этих точках таковы: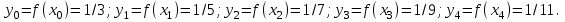 Далее найдем числовое значение интеграла, пользуясь формулой (23):
Далее найдем числовое значение интеграла, пользуясь формулой (23):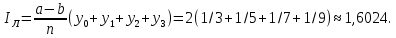
Если вычисление определенного интеграла произвести по формуле (24), то получим:
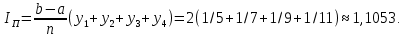
Метод центральных прямоугольников:
(по сути, не берем самое первое и самое последнее значение т.е. если значений 6, то y0 и y5)
Формула для приближенного вычисления определенного интеграла функции f(x) на интервале [a, b] с использованием равномерной сетки:
∫[a, b] f(x) dx ≈ h * (f(x₁/₂) + f(x₃/₂) + ... + f(xₙ₋₁/₂))
Пример:
Рассмотрим функцию f(x) = x^2 на интервале [0, 1].
Шаг сетки: h = (1 - 0) / 4 = 0.25
Точки на сетке: x₀ = 0, x₁/₂ = 0.125, x₁ = 0.25, x₃/₂ = 0.375, x₂ = 0.5, x₅/₂ = 0.625, x₃ = 0.75, x₇/₂ = 0.875, x₄ = 1
Подставляем значения в формулу:
∫[0, 1] x^2 dx ≈ 0.25 * (f(0.125) + f(0.375) + f(0.625) + f(0.875))
≈ 0.25 * (0.015625 + 0.140625 + 0.390625 + 0.765625)
≈ 0.328125
Метод трапеций:
Формула для приближенного вычисления определенного интеграла функции f(x) на интервале [a, b] с использованием равномерной сетки:
∫[a, b] f(x) dx ≈ h/2 * (f(x₀) + 2f(x₁) + 2f(x₂) + ... + 2f(xₙ₋₁) + f(xₙ))
Пример:
Рассмотрим функцию f(x) = x^2 на интервале [0, 1].
Шаг сетки: h = (1 - 0) / 4 = 0.25
Точки на сетке: x₀ = 0, x₁ = 0.25, x₂ = 0.5, x₃ = 0.75, x₄ = 1
Подставляем значения в формулу:
∫[0, 1] x^2 dx ≈ 0.25/2 * (f(0) + 2f(0.25) + 2f(0.5) + 2f(0.75) + f(1))
≈ 0.25/2 * (0 + 20.0625 + 20.25 + 2*0.5625 + 1)
≈ 0.265625
Метод Симпсона:
Формула для приближенного вычисления определенного интеграла функции f(x) на интервале [a, b] с использованием равномерной сетки:
∫[a, b] f(x) dx ≈ h/3 * (f(x₀) + 4f(x₁) + 2f(x₂) + 4f(x₃) + ... + 2f(xₙ₋₂) + 4f(xₙ₋₁) + f(xₙ))
Пример:
Рассмотрим функцию f(x) = x^2 на интервале [0, 1].
Шаг сетки: h = (1 - 0) / 4 = 0.25
Точки на сетке: x₀ = 0, x₁ = 0.25, x₂ = 0.5, x₃ = 0.75, x₄ = 1
Подставляем значения в формулу:
∫[0, 1] x^2 dx ≈ 0.25/3 * (f(0) + 4f(0.25) + 2f(0.5) + 4f(0.75) + f(1))
≈ 0.25/3 * (0 + 40.0625 + 20.25 + 4*0.5625 + 1)
≈ 0.28125
Метод решения дифференциальных уравнений
Один из наиболее распространенных вариантов метода Рунге-Кутта - это метод Рунге-Кутта четвертого порядка, который использует четыре стадии. Давайте рассмотрим пример применения этого метода для численного решения простого дифференциального уравнения первого порядка:
dy/dx = x
Для этого уравнения известно точное аналитическое решение: y(x) = (1/2) * x^2 + C, где C - произвольная постоянная.
Процесс решения с использованием метода Рунге-Кутта четвертого порядка состоит из следующих шагов:
-
Задайте начальные условия: значение x0 и соответствующее значение y0. -
Задайте конечную точку x, до которой нужно вычислить решение. -
Задайте шаг интегрирования h. -
Выполните итерационные шаги метода Рунге-Кутта до достижения конечной точки x.
На каждом шаге вычислите коэффициенты k1, k2, k3 и k4:
k1 = h * f(x, y)
k2 = h * f(x + h/2, y + k1/2)
k3 = h * f(x + h/2, y + k2/2)
k4 = h * f(x + h, y + k3)
-
Обновите значения x и y:
x = x + h
y = y + (k1 + 2k2 + 2k3 + k4)/6
-
Повторите шаги, пока x не достигнет конечной точки. -
Получите численное решение y(x) после достижения конечной точки.
Давайте рассмотрим пример применения метода Эйлера для численного решения простого дифференциального уравнения первого порядка:
dy/dx = x
Для этого уравнения известно точное аналитическое решение: y(x) = (1/2) * x^2 + C, где C - произвольная постоянная.
Процесс решения с использованием метода Эйлера состоит из следующих шагов:
-
Задайте начальные условия:
значение x0 и соответствующее значение y0.
-
Задайте конечную точку x, до которой нужно вычислить решение. -
Задайте шаг интегрирования h. -
Выполните итерационные шаги метода Эйлера до достижения конечной точки x.
На каждом шаге вычислите приближенное значение изменения y:
delta_y = h * f(x, y)
Обновите значения x и y:
x = x + h
y = y + delta_y
Повторите шаги, пока x не достигнет конечной точки.
-
Получите численное решение y(x) после достижения конечной точки.
Метод Адамса требует предварительного вычисления начальных значений с использованием другого численного метода, например, метода Рунге-Кутта. Затем он использует рекуррентное соотношение для вычисления следующего значения решения.
Давайте рассмотрим пример применения метода Адамса для численного решения простого дифференциального уравнения первого порядка:
dy/dx = x
Для этого уравнения известно точное аналитическое решение: y(x) = (1/2) * x^2 + C, где C - произвольная постоянная.
Процесс решения с использованием метода Адамса состоит из следующих шагов:
-
Задайте начальные условия: значение x0 и соответствующее значение y0. -
Задайте конечную точку x, до которой нужно вычислить решение. -
Задайте шаг интегрирования h. -
Используйте другой численный метод, например, метод Рунге-Кутта, для вычисления начальных значений.
Вычислите первые несколько значений решения с использованием метода Рунге-Кутта.
-
Выполните итерационные шаги метода Адамса до достижения конечной точки x.
На каждом шаге вычислите приближенное значение изменения y:
delta_y = h * f(x, y)
Обновите значения x и y:
x = x + h
y = y + delta_y
Используйте предыдущие значения решения для вычисления следующего значения с использованием рекуррентного соотношения метода Адамса.
Повторите шаги, пока x не достигнет конечной точки.
-
Получите численное решение y(x) после достижения конечной точки.