Файл: Лабораторная работа Определение коэффициента динамической вязкости жидкости методом Стокса.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 24.10.2023

Просмотров: 366

Скачиваний: 16

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Лабораторная работа 4.1.


«Определение коэффициента динамической вязкости жидкости методом Стокса»

Цель работы - изучение явления внутреннего трения в жидкостях и опытное определение величины коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке.

Описание экспериментальной установки

Установка для реализации метода Стокса состоит из стеклянного цилиндра 1, в котором находится исследуемая жидкость, вязкость которой необходимо определить (рис. 1).



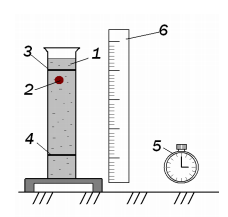
Рис. 1. Установка для измерения вязкости жидкости по методу Стокса

На цилиндре имеются метки 3 и 4. Расстояние между метками L можно замерить при помощи линейки 6, а диаметр шарика – при помощи микрометра. Время прохождения между метками 3 и 4 можно определить с помощью секундомера 5. Метка 3 помещена на несколько сантиметров ниже верхнего уровня жидкости для выполнения условия равномерного движения шарика в жидкости; V = const на участке L. Цилиндр закрыт пробкой с воронкой, в которую опускается шарик, двигающийся в дальнейшем примерно по оси цилиндра так, чтобы на его движение не влияли стенки. При более точных измерениях необходимо учитывать влияние размеров стеклянного цилиндра. Исследуемой жидкостью является глицерин, плотность которого ж = (1,260,01)103 кг/м^3 . Исследуемые шарики – стальные с плотностью ш = (7,80,1)103 кг/м^3 . Эксперимент можно проводить как на физической, так и на виртуальной модели установки.

Рабочая формула.



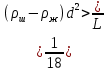
L=64-69

d=6,2-6,7

Погрешности:

Абсолютные приборные погрешности прямых измерений:

ΔL = 0,005 м

Δd = 0,00005 м

Δt = 0,1 м

Δж = 0,01E3 кг/м^3

Δш = 0,1E3 кг/м^3

Относительные погрешности измерений:

L = ΔL/L

L1 = 0,005/0,64 = 0,0078

L2 = 0,005/0,64 = 0,0078

L3 = 0,005/0,69 = 0,0072

L4 = 0,005/0,69 = 0,0072

L5 = 0,005/0,66 = 0,0077

d = Δd/d

d1 = 0,00005/0,0062 = 0,0081

d2
= 0,00005/0,0067 = 0,0075

d3 = 0,00005/0,0062 = 0,0081

d4 = 0,00005/0,0067 = 0,0075

d5 = 0,00005/0,0065 = 0,0077

t = Δt/t

t1 = 0,1/6,9 = 0,0145

t2 = 0,1/6,0 = 0,0167

t3 = 0,1/7,4 = 0,0135

t4 = 0,1/6,4 = 0,0156

t5 = 0,1/7,5 = 0,0154

= Δ/

1 = 2 = 3 = 4 =5 = 6 = 0,01/1,26 = 0,008

V = L/t

V1 = L1/t1 = 0,64/6,9 = 0,09 м/с

V2 = L1/t1 = 0,64/6,0 = 0,11 м/с

V3 = L1/t1 = 0,69/7,4 = 0,09 м/с

V4 = L1/t1 = 0,69/6,4 = 0,11 м/с

V5 = L1/t1 = 0,66/6,5 = 0,10 м/с


1 = 1/18*(7,8E3-1,26E3)*0,0062^2*9,81/0,09 = 1,48 Па*с

2 = 1/18*(7,8E3-1,26E3)*0,0067^2*9,81/0,11 = 1,50 Па*с

3 = 1/18*(7,8E3-1,26E3)*0,0062^2*9,81/0,09 = 1,47 Па*с

4 = 1/18*(7,8E3-1,26E3)*0,0067^2*9,81/0,11 = 1,48 Па*с

5 = 1/18*(7,8E3-1,26E3)*0,0065^2*9,81/0,10 = 1,48 Па*с

= (1,48+1,50+1,47+1,48+1,48)/5 = 1,48 Па*с

Re = ж*V*d/

Re1 = 1,26E3*0,09*0,0062/1,48 = 0,49

Re2 = 1,26E3*0,11*0,0067/1,50 = 0,60

Re3 = 1,26E3*0,09*0,0062/1,47 = 0,50

Re4 = 1,26E3*0,11*0,0067/1,48 = 0,61

Re5 = 1,26E3*0,10*0,0065/1,48 = 0,56

Таблица 1 – Результаты измерений

№ п/п
L, м
ΔL, м
d, м
Δd, м
t,с
Δt, с
V, м/с
Re
, Па*c
Δ, Па*c
, Па*с

1
0,6400
0,005
0,00620
0,00005
6,9
0,1
0,09
0,49
1,48
0,037
1,48

2
0,6400
0,005
0,00670
0,00005
6
0,1
0,11
0,60
1,50
0,038

3
0,6900
0,005
0,00620
0,00005
7,4
0,1
0,09
0,50
1,47
0,036

4
0,6900
0,005
0,00670
0,00005
6,4
0,1
0,11
0,61
1,48
0,037

5
0,6600
0,005
0,00650
0,00005
6,5
0,1
0,10
0,56
1,48
0,037

Среднее
1,48
0,037
 



Таблица 2 – Расчет относительных погрешностей

№ п/п
L, м
ΔL, м
d, м
Δd, м
t,с
Δt, с
L
d
t


1
0,6400
0,005
0,00620
0,00005
6,9
0,1
0,0078
0,0081
0,0145
0,008

2
0,6400
0,005
0,00670
0,00005
6
0,1
0,0078
0,0075
0,0167
0,008

3
0,6900
0,005
0,00620
0,00005
7,4
0,1
0,0072
0,0081
0,0135
0,008

4
0,6900
0,005
0,00670
0,00005
6,4
0,1
0,0072
0,0075
0,0156
0,008

5
0,6600
0,005
0,00650
0,00005
6,5
0,1
0,0076
0,0077
0,0154
0,008

Оценка абсолютной погрешности коэффициента вязкости

По стандартной методике



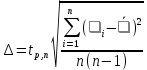
t0,95;5 = 2,57

№ п/п
(i- )^2

1
0,00003

2
0,00030

3
0,00018

4
0,00000

5
0,00000



0,00051

/(n*(n-1))
0,00003

(/(n*(n-1)))^0,5
0,00505


Δ = 2,57*0,00505 = 0,013

по методике расчёта погрешностей косвенных измерений как

L
d
t


0,0078
0,0081
0,0145
0,008

0,0078
0,0075
0,0167
0,008

0,0072
0,0081
0,0135
0,008

0,0072
0,0075
0,0156
0,008

0,0076
0,0077
0,0154
0,008




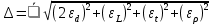
Δ1 = 1,48*((2*0,0081)^2+0,0078^2+0,0145^2+0,008^2)^0,5 = 0,037

Δ2 = 1,48*((2*0,0075)^2+0,0078^2+0,0167^2+0,008^2)^0,5 = 0,038

Δ3 = 1,48*((2*0,0081)^2+0,0072^2+0,0135^2+0,008^2)^0,5 = 0,036

Δ4 = 1,48*((2*0,0075)^2+0,0072^2+0,0156^2+0,008^2)^0,5 = 0,037

Δ5 = 1,48*((2*0,0077)^2+0,0076^2+0,0154^2+0,008^2)^0,5 = 0,037

Δ = 0,037

конечный результат

 =

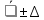
 = (1,48 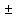0,04) Па*с

Вывод: изучили явления внутреннего трения в жидкостях и опытным путем определили величину коэффициента вязкости жидкости методом Стокса на виртуальной лабораторной установке, коэффициента вязкости жидкости соответствует глицерину при t = 200C.
Контрольные вопросы

Поясните сущность явления вязкого трения. Какова природа сил внутреннего трения жидкости?

Вязкость или внутреннее трение – свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Это явление определяет диссипацию (поглощение) энергии при деформации среды. При деформации сдвига вязкость называют сдвиговой. При деформации объема (всестороннее сжатие) проявляется объемная вязкость. В данном случае мы будем касаться только вопроса сдвиговой вязкости.

Суть явления состоит в том, что движущиеся слои газа или жидкости увлекают соседние слои и, наоборот, неподвижные (или движущиеся с меньшей скоростью) тормозят более быстрые соседние слои. Таким образом, между любыми соседними слоями рассматриваемой среды действуют силы внутреннего трения (или силы вязкости). Механизм возникновения этих сил заключается в переносе импульса (количества движения) от одного слоя к другому.

Что такое коэффициент динамической вязкости? В каких единицах измеряется величина вязкости в системе СИ?
Коэффициентом динамической вязкости называется величина, численно равная силе внутреннего трения, с которой один слой увлекает или тормозит другой слой жидкости при условии, что площадь соприкосновения слоев S=1 и градиент скорости dv/dx = 1.

В системе СИ за единицу динамической вязкости принимают 1 Па*с - вязкость такой среды, в которой один слой увлекает или тормозит другой с силой в 1 Н, если площадь соприкосновения слоев S = 1 м^2 и градиент скорости dv/dx = 1 м/c^2.
Какие силы действуют на тело, движущееся в жидкости?
На тело, погруженное в жидкость и остающееся в равновесии на плаву действуют две силы: сила тяжести и равная ей выталкивающая сила (и равная весу жидкости, вытесненной погруженным объёмом тела).
На тело, погруженное в жидкость и тонущее действуют три силы: сила тяжести, неравная ей (меньше) выталкивающая сила (равная весу жидкости, вытесненной погруженным объёмом тела), а также сила трения при движении, в значительной степени зависящая от скорости погружения и вязкости жидкости.
На тело, погруженное в жидкость и лежащее плотно на дне, действуют три силы: сила тяжести, неравная ей выталкивающая сила, и сила реакции со стороны дна. В данном случае выталкивающая сила уменьшается на величину, равную весу жидкости, занимаемому той частью объёма тела, под которой нет воды
Дайте определение ламинарного и турбулентного течения жидкости.
Турбулентным называется такое течение жидкости, при котором её частицы совершают неустановившееся и неупорядоченные движения по сложным траекториям, приводящим к перемешиванию слоёв.

Ламинарное – это упорядоченное течение жидкости, при котором траектории движения соседних частиц мало отличаются друг от друга.
Запишите формулу Стокса и укажите условия ее применимости.
Для тел сферической формы модуль силы вязкого трения определяется формулой Стокса

Смотрите также файлы