ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 23
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Оглавление
1.Архитектура массивно-параллельных компьютеров 2
2.Анализ моделей и методов размещения в коммутационном- монтажном проектирование 4
3.Акселератор планирования размещения задач в кластерных вычислительных системах высокой готовности 6
1.Архитектура массивно-параллельных компьютеров
MPP (massive parallel processing) – массивно-параллельная архитектура. Главная особенность такой архитектуры состоит в том, что память физически разделена. В этом случае система строится из отдельных модулей, содержащих процессор, локальный банк операционной памяти (ОП), коммуникационные процессоры(роутеры) или сетевые адаптеры, иногда – жесткие диски и/или другие устройства ввода/вывода. По сути, такие модули представляют собой полнофункциональные компьютеры (см. рис. 1).
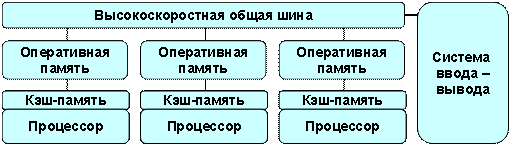
Рисунок 1 – Схематический вид архитектуры с раздельной памятью
Доступ к банку ОП из данного модуля имеют только процессоры (ЦП) из этого же модуля. Модули соединяются специальными коммуникационными каналами. Пользователь может определить логический номер процессора, к которому он подключен, и организовать обмен сообщениями с другими процессорами.
Используются два варианта работы операционной системы на машинах MPP-архитектуры:
- полноценная операционная система (ОС) работает только на управляющей машине (front-end), на каждом отдельном модуле функционирует сильно урезанный вариант ОС, обеспечивающий работу только расположенной в нем ветви параллельного приложения.
- на каждом модуле работает полноценная UNIX-подобная ОС, устанавливаемая отдельно.
Главным преимуществом систем с раздельной памятью является хорошая масштабируемость: в отличие от SMP-систем, в машинах с раздельной памятью каждый процессор имеет доступ только к своей локальной памяти, в связи с чем не возникает необходимости в потактовой синхронизации процессоров. Практически все рекорды по производительности на сегодня устанавливаются на машинах именно такой архитектуры, состоящих из нескольких тысяч процессоров (ASCI Red, ASCI Blue Pacific).
Недостатки:
- отсутствие общей памяти заметно снижает скорость межпроцессорного обмена, поскольку нет общей среды для хранения данных, предназначенных для обмена между процессорами. Требуется специальная техника программирования для реализации обмена сообщениями между процессорами;
- каждый процессор может использовать только ограниченный объем локального банка памяти;
- вследствие указанных архитектурных недостатков требуются значительные усилия для того, чтобы максимально использовать системные ресурсы. Именно этим определяется высокая цена программного обеспечения для массивно-параллельных систем с раздельной памятью.
Системами с раздельной памятью являются суперкомпьютеры МВС-1000, IBM RS/6000 SP, SGI/CRAY T3E, системы ASCI, Hitachi SR8000, системы Parsytec. Машины последней серии CRAY T3E от SGI, основанные на базе процессоров Dec Alpha 21164 с пиковой производительностью 1200 Мфлопс/с (CRAY T3E-1200), способны масштабироваться до 2048 процессоров.
При работе с MPP-системами используют так называемую Massive Passing Programming Paradigm – парадигму программирования с передачей данных (MPI, PVM, BSPlib).
Выбор типа драйвера для каждого магистрального сигнала (приемник, передатчик или приемопередатчик) определяется назначением этого сигнала и возможными режимами работы УС. Так, например, в случае, когда УС работает в режиме программного обмена, приемники используются для сигналов адреса SA0 ... SA9 и для управляющих сигналов -IOR, -IOW, AEN, BALE, -SBHE, передатчики используются для I/O СН RDY и -I/O CS 16. Для сигналов данных могут использоваться приемники (если УС работает только в режиме записи), передатчики (если УС работает только в режиме чтения) или приемопередатчики (если УС работает как в режиме чтения, так и в режиме записи). Если возможен обмен по прерываниям, то добавляется передатчик для сигнала IRQ, а если применяется ПДП, то применяется передатчик для сигнала DRQ и приемник для сигнала DACK.
Остановимся подробнее на характеристиках микросхем, которые могут применяться для буферирования.
Приемники магистральных сигналов должны удовлетворять двум основным требованиям: малые входные токи и высокое быстродействие (они должны успевать отрабатывать в течение отведенных им временных интервалов циклов обмена).
Конкретное значение допустимых времен задержек определяется используемой схемой интерфейсной части УС в целом, но можно определенно сказать, что микросхемы обычных (не быстродействующих) КМОП серий здесь не годятся, несмотря на их малые входные токи. Не подходят и микросхемы серии К155 (SN74) из-за их больших входных токов.
Требованиям, предъявляемым к приемникам, удовлетворяют следующие серии микросхем: КР1533 (SN74ALS), К555 (SN74LS) и КР1554 (74АС). Величины входных токов логического нуля для них составляют соответственно 0,2 мА, 0,4 мА и 0,2 мА, а величины временных задержек не превышают соответственно 15 не, 20 не и 10 не. Помимо этих серий в качестве приемников можно использовать специальные микросхемы магистральных приемников серии КР559 (входной ток не более 0,12 мА, задержка не более 30 не). Требованиям, предъявляемым к приемникам, удовлетворяют также микросхемы электрически программируемых ППЗУ и ПЛМ серии КР556 (136, N82S, DM87S, НМ76). Это тоже немаловажно, так как их очень удобно использовать в схемах селекторов адреса УС. Входные токи этих микросхем не превышают 0,25 мА. Пример входного буфера показан на рис1.
Малые входные токи микросхем серий КР1533 и КР1554 позволяют подключать к линии магистрали даже два входа таких микросхем.
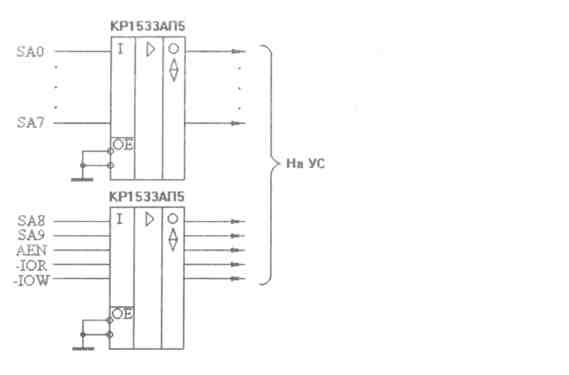
Рис. 1-Пример входного буфера.
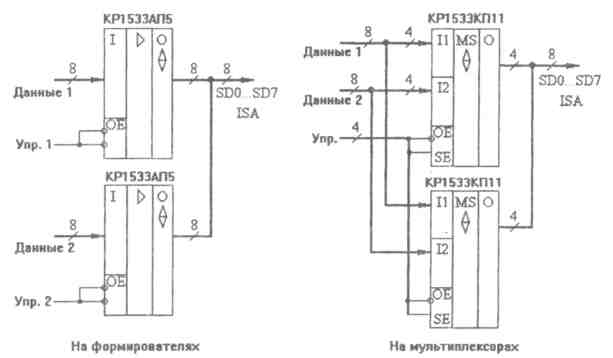
Рис. 2 - Мультиплексирование шины данных.
Теперь переходим к передатчикам. Требования к ним: большой выходной ток и высокое быстродействие. Часто они должны иметь также отключаемый выход (например, для шины данных), то есть иметь выход с открытым коллектором или с тремя состояниями. Это связано с необходимостью перехода УС в пассивное состояние в случае отсутствия обращения к нему. Выбор микросхем передатчиков гораздо больше, такие микросхемы есть практически в каждой серии (К155, К555, КР1533, К559 и т.д.).
Передатчики часто выполняют функцию мультиплексирования данных, которые должны поступать на шину данных ISA от различных источников. На рис. 2. упрощенно показано два наиболее распространенных подхода к решению данной задачи (для 8-разрядной шины данных). Отметим, что при использовании микросхем мультиплексоров надо брать те из них, которые имеют выходы с тремя состояниями и большие выходные токи.
И, наконец, приемопередатчики. Требования к ним включают в себя требования к приемникам и передатчикам, то есть малый входной ток, большой выходной ток, высокое быстродействие и обязательное отключение выходов. Надо отметить, что в простейшем случае (когда разрядов немного) приемопередатчики могут быть построены на микросхемах приемников и передатчиков с отключаемыми выходами. Однако при большом количестве разрядов надо использовать специальные микросхемы приемопередатчиков. Эти микросхемы бывают двух основных типов (рис. 3): с двумя двунаправленными шинами или с тремя шинами (одной двунаправленной, одной входной шиной и одной выходной шиной).
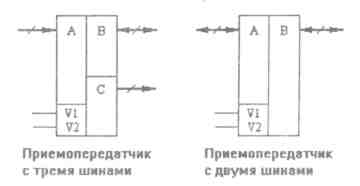
Рис.3. Типы приемопередатчиков.
Для управления работой приемопередатчиков используются два управляющих сигнала. Характеристики некоторых приемопередатчиков сведены в таблицу 1. В ней указаны разрядность шин, величины задержек и входных/выходных токов всех шин микросхем. В табл. 2. приведены режимы работы в зависимости от управляющих сигналов. Отметим такую особенность микросхемы КР59ИПЗ, как невозможность одновременного отключения ее двунаправленной и выходной шин. В таблице использованы следующие обозначения: ОК — выход с открытым коллектором, ЗС — выход с тремя состояниями. Отметим, что если приемопередатчики с открытым коллектором используются для буферирования шины данных, то на их выходах необходимо включать резисторы на шину +5В (если они не работают на линию, к которой эти резисторы уже подключены). Поэтому их применение иногда оказывается нежелательным. Это однако совсем не означает, что они не могут быть использованы, например, в операционной части УС. Особенностью микросхемы КР580ВА86 (87) является то, что шины имеют различные выходные токи, и только одна из них (В) удовлетворяет требованиям стандарта ISA. У других микросхем все двунаправленные шины выдают требуемые выходные токи. Те или иные сигналы управления могут быть более или менее удобны в каждом конкретном случае.
Табл. 1. Характеристики приемопередатчиков.
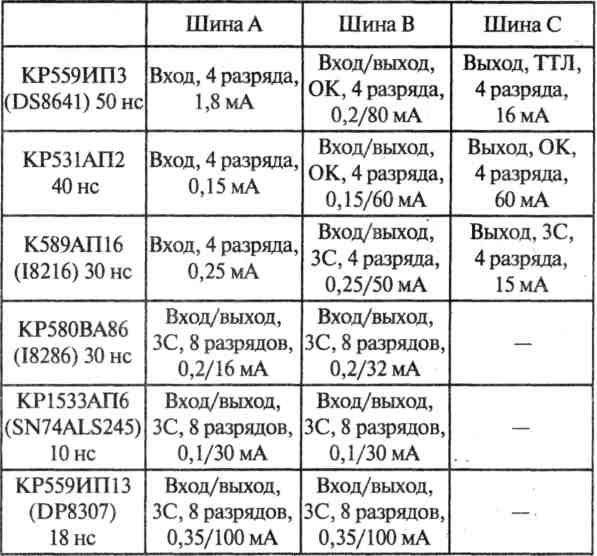
Табл. 2. Микросхемы приемопередатчиков.
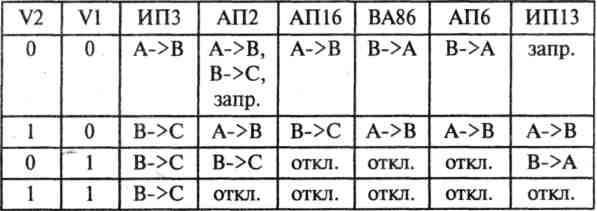
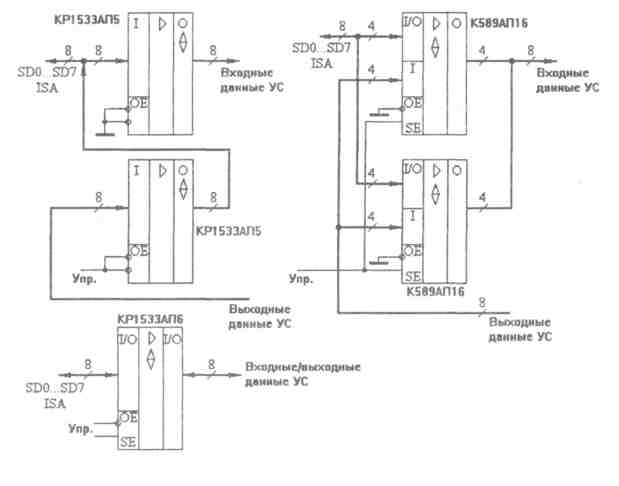
Рис. 4. Варианты построения приемопередатчиков данных.
В приемопередатчике с двумя шинами и на приемопередатчике с тремя шинами (для 8-разрядных данных).
Чаще нужны приемопередатчики с раздельными входными и выходными шинами данных УС, но при использовании многоразрядных микросхем ОЗУ или сдвиговых регистров типа КР1533ИР24 (SN74ALS299), которые имеют двунаправленную шину данных, удобнее применять приемопередатчики с совмещенными входными/выходными данными УС.
2.Анализ моделей и методов размещения в коммутационном- монтажном проектирование
Монтажно-коммутационное пространство (МКП) предназначено для размещения конструктивных модулей и трассировки соединений между их контактами, которые должны быть соединены электрическими цепями. Форма и, естественно, математическая модель МКП зависят от уровня модуля, для которого в данный момент решаются задачи конструирования (базовый матричный кристалл, печатная плата, панель и т. д.). В дальнейшем ограничимся только плоским монтажно-коммутационным пространством, соответствующим конструктивному модулю типа печатной платы.
Без потери общности будем считать, что пространство имеет прямоугольную форму, так как введением областей, в которых запрещается размещение конструктивных модулей более низкого уровня или трассировки соединений, можно придать пространству произвольную форму. Так как МКП служит для решения двух задач — размещения модулей и трассировки, — то модели МКП, используемые для решения каждой задачи, будут иметь отличия. Рассмотрим эти модели подробнее.
Наибольшее распространение для решения задач размещения конструктивных модулей в плоском МКП получили эвристические дискретные модели. Такие модели (будем их называть МКП1) строятся следующим образом: МКП разбивается на элементарные площадки (дискреты), каждая из которых предназначена для размещения одного конструктивного модуля более низкого уровня, например микросхемы на печатной плате. Эти площадки в дальнейшем будем называть дискретами рабочего поля (ДРП).
Каждый дискрет в процессе решения задачи размещения может находиться в одном из следующих состояний: свободен для размещения, занят, имеет определенный вес, запрещающий размещение в нем модуля, и т. д. Такая модель МКП отличается простотой и удобством использования в эвристических алгоритмах размещения, однако она не является полностью формализованной.
Одной из разновидностей модели МКП1 является модель с ортогональной сеткой, в узлах которой могут размещаться модули низкого уровня (рис. 2). Шаг сетки выбирается из условия возможности размещения модулей в соседних узлах сетки.
При размещении разногабаритных компонентов часто размер ДРП выбирают равным наибольшему общему делителю линейных размеров размещаемых модулей либо линейным размерам установочного места для наименьшего из модулей, если размеры всех модулей кратны. Заметим, что выбор шага дискретизации представляется весьма важным, так как при малых размерах ДРП увеличивается время решения задачи, зато повышается плотность заполнения МКП модулями низшего уровня.
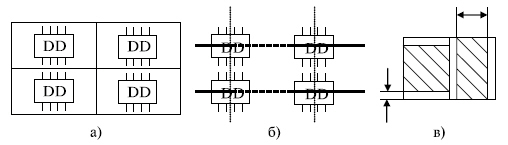
Рис. 2 - Дискретные модели МКП
Аналогичные дискретные модели используются и для решения задач трассировки. В этом случае дискрет является квадратом со сторонами, равными ширине проводника плюс зазор между ними. При этом считается, что проводник из каждого дискрета может быть проведен только в соседний ДРП.
Наибольшее распространение для решения задач размещения получили модели МКП в виде взвешенного графа VG(S, V), которые будем обозначать МКП2. Взвешенный граф VG представляет собой симметрический граф, в котором множество вершин S соответствует множеству установочных позиций в коммутационном пространстве для модулей низшего уровня, а множество ветвей интерпретирует множество связей между соответствующими установочными позициями. Каждой ветви графа uij присваивается вес pij — он равен числу условных единиц расстояния между центрами установочных позиций Si и Sj, интерпретируемых вершинами, которые инцидентны данной ветви. Вес ветви pij определяется в зависимости от метрики пространства по одной из формул.
Для описания взвешенного графа VG удобно использовать матрицу смежностей Q, строки и столбцы которой соответствуют вершинам графа, т. е. множеству установочных позиций в МКП, а элементы gij равны весу ветви, инцидентной i-й и j-й вершинам графа. Элементы, лежащие на главной диагонали матрицы смежностей Q, принимаются равными нулю.
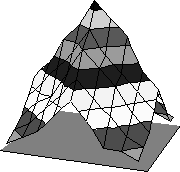
Рис.1.Модель распределения трасс на монтажно-коммутационном поле
3.Акселератор планирования размещения задач в кластерных вычислительных системах высокой готовности
С началом разработки отказоустойчивых многокомпьютерных и высокодоступных кластеров возрастают требования к скорости выполнения шагов планирования развертывания задач [1-4]. Быстрое восстановление правильного функционирования системы путем отключения неисправного процессора и перенастройки структуры системы путем замены его резервным процессором, обычно не относящимся к процессорам обработки Ваша конфигурация подключения существенно изменится. Формирование длинных маршрутов передачи данных. Их можно уменьшить путем перераспределения оперативных задач.
В то же время этапы планирования развертывания носят комбинаторный характер и отличаются высокой вычислительной сложностью, что может привести к значительному увеличению времени восстановления и снижению коэффициентов готовности системы. По этой причине не рекомендуется отказывать в переназначении задач до перезагрузки восстановленной системы. Это связано с тем, что увеличение задержек связи может привести к потерям производительности системы, которые превышают ожидаемые выгоды от использования интерактивной многопроцессорной параллельной многопроцессорной обработки. программа.
Следовательно, для сокращения времени восстановления многопроцессорной кластерной системы необходимо значительно сократить время, затрачиваемое на планирование размещения задач по сравнению с программной реализацией на управляющей машине кластера. Этого можно добиться, создав специальный ускоритель. При разработке алгоритмов этой функции целесообразно найти новые способы снижения вычислительной сложности процедуры планирования размещения задач на высокопроцессорных матричных блоках.
В связи с началом освоения отказоустойчивых мультикомпьютеров и кластеров высокой готовности повышаются требования к скорости выполнения процедур планирования размещения задач. Быстрое восстановление правильности функционирования системы путем реконфигурации ее структуры с отключением неисправного процессора и заменой его резервным, расположенным обычно вне поля обрабатывающих процессоров, приводит к существенному изменению конфигурации связей между ними и образованию длинных и перекрывающихся маршрутов передачи данных. Они могут быть уменьшены и разнесены путем оперативного переразмещения задач. В то же время процедуры планирования размещения являются комбинаторными, имеют большую вычислительную сложность и поэтому могут привести к существенному увеличению времени восстановления и снижению коэффициента готовности системы. Отказываться из-за этого от переразмещения задач перед рестартом восстанавливаемой системы нецелесообразно, так как возросшие коммуникационные задержки могут привести к такой потере системной производительности, которая превысит ожидаемый выигрыш от применения параллельной многопроцессорной обработки комплекса взаимодействующих программ. Поэтому для уменьшения времени восстановления многопроцессорных кластерных систем необходимо многократно снизить затраты времени на планирование размещения задач. Этого можно достичь путем создания специализированного ускоряющего вычислительного устройства (акселератора), а при разработке алгоритмов его функционирования целесообразно найти новый метод снижения вычислительной сложности процедур планирования размещения задач по процессорам матричных базовых блоков кластерных систем высокой готовности.
В связи с вышеизложенным актуальной является научно-техническая задача многократного повышения скорости выполнения процедур планирования размещения параллельно обрабатываемых задач по процессорам кластерной системы путем реализации названных процедур в специализированном вычислительном устройстве.
Разработанный метод ускорения поиска субоптимального варианта размещения задач по процессорам базового матричного кластерного блока основан на следующем подходе.
Пакет взаимодействующих программ (задач), запланированных к обработке в базовом блоке, аописывается графом взаимодействия задач
G=
а - аа (1)множество вершин графа G, вершины
акоторого соответствуюта задачам, а дуги связей между ними 
апри 
авзвешиваются объёмами данных 
, передаваемыми между задачами и сведенными в матрицу обмена информацией (МОИ) 
, где 
.Матричный базовый блок кластерной системы представляется топологической моделью в виде графа H=
, где
а - множество идентификаторова процессорных модулей базового блока, организованных в матрицу |P|n?n, где 
а- число процессорных модулей базового блока; 
- множество межмодульных связей, задаваемых матрицей смежности 
аразмером 
.Размещение пакета программ (задач), описываемых графом G (1), в параллельной системе (ПС) может быть аналитически описано отображением
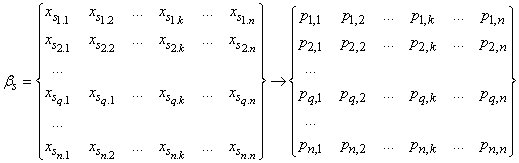 ,где  ,  ,  . | (2) |
Здесь
а - это номер очередной перестановки задач 
апо процессорным модулям 
, соответствующий -му варианту размещения. Мощность множества 
авсевозможных отображений (2) равна числу всевозможных перестановок задач 
ав матрице 
:
. Для описания множества длин 
акратчайших маршрутов передачи данных в пределах базового блока введем матрицу минимальных расстояний (ММР) 
, 
, которая строится по матрице смежности.Задачу планирования размещения, можно сформулировать как поиск такого отображения b*IY, что
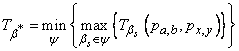, (3)где а
а - коммуникационная задержка при передаче данных между процессорными модулями 
аи 
, соответствующая отображению 
аи вычисляемая как произведение
,а (4)где
аи 
,а
.аа (5)Присутствующий в (4) сомножитель С не учитывается в выражениях (3,5) и последующем анализе, так как он обратно пропорционален постоянной скорости передачи данных и поэтому не влияет на результаты минимизации по (3).
Поиск наилучшего варианта размещения b* по критерию (3) является сложной переборной задачей. Одним из путей его ускорения может быть применение целенаправленных перестановок строк и столбцов матрицы МОИ с выбором в ней aк-го места перестановки ее элемента
апо критерию:
, аа (6)где
а - одноименные элементы матрицы ММР; а - элемент МОИ, которому соответствует 
, найденный в предыдущем шаге перестановок.Новизна подхода состоит в том, что общее число требуемых перестановок можно дополнительно уменьшить, если отбросить явно нецелесообразные из них, разрешая очередную перестановку по следующим дополнительным критериям:
,аа (7)
.аа (8)Многократное ускорение поиска возможно за счет допустимого снижения выигрыша на снижение величины коммуникационной задержки, например, не более, чем на 20-30%, по сравнению с лучшими результатами, достигаемыми при больших затратах времени на поиск. Для этого необходимо в ходе поиска контролировать степень уменьшения величины образующейся коммуникационной задержки (3) и принимать решение о целесообразности продолжения поисковых перестановок строк и столбцов матрицы МОИ. Процедура принятия решения основана на вычислении недостижимой минимальной оценки размещения Tinf (гипотетического минимума коммуникационной задержки) при допущении, что топологии графов G и H тождественны. При вычислении нижней оценки будем назначать дуги графа G с наибольшим весом
ана самые короткие маршруты в графе H, не обращая внимания на ограничения, накладываемые фактическими связями между задачами в графе G. Соответствующий формализованный алгоритм выглядит следующим образом.-
Переписать элементы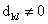
аматрицы D в вектор-строку 
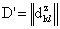атак, что 
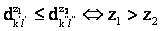, где z1 и z2 - порядковые номера элементов в D'. -
Переписать элементы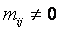
аматрицы M в вектор-строку 
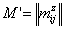атак, что 
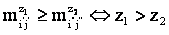, где z1 и z2 - порядковые номера элементов в M'. -
Положить
,гдеа
, а 
- мощность множества E, равная количеству дуг в графе G; 
, 
а - одноименные элементы векторов 
аи 
ас одинаковыми порядковыми номерами от начала названных выше векторЦстрок.Для многократного ускорения поиска разработана следующая методика ускоренного выполнения процедур планирования размещения задач.
1. Составляются две матрицы: обмена информацией между задачами (МОИ) и кратчайших маршрутов (ММР) между процессорами в коммуникационной среде базового блока.
2. Вычисляются гипотетический минимум коммуникационной задержки Tinf и коэффициент эффективности исходного произвольного размещения задач
=Tн/Тinf.3. По порогу эффективности
апринимается решение о целесообразности инициализации процедуры поиска субоптимального размещения. Под коэффициентом эффективности перестановок 
апонимается отношение реально полученной величины задержки (5) к гипотетической 
.4. Выполняются шаги целенаправленных перестановок столбцов и строк матрицы обмена информацией. Находится максимальное значение коммуникационной задержки (5) по предыдущему варианту перестановок задач.
5. Находится минимум (3) из максимумов задержек по всем вариантам перестановок и вычисляется коэффициент эффективности
.6. Если
аоказывается менее установленного порога эффективности 
, шаги поиска прекращаются и найденный вариант матрицы обмена информацией считается соответствующим субоптимальному размещению.Величина порога эффективности
, выбрана в результате статических исследований на программной модели алгоритма функционирования АПР.На основании разработанных в данной главе метода ускорения поиска и методики ускорения выполнения процедур планирования размещения составлен следующий алгоритм, программноЦаппаратно реализованный в двухуровневом микропроцессорном акселераторе.
-
Ввести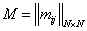
, 
, 
, 
, 
, 
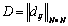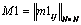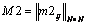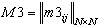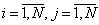а"mij=0, "m1ij=0, "m2ij=0, "m3ij=0.
2. Переписать "mij в
=
ас изменением порядка следования элементов так, что 
, где z1 и z2 порядковые номера элементов .3. Переписать "dij в
=
ас изменением порядка следования элементов так, что 
, где z1 и z2 порядковые номера элементов .Положить
, где 
, 
.5. Найти
, где N - число задач.6. Вычислить
. Если 
, то останов, иначе перейти к п.7.7. Принять Т0=Тн.
8. Выполнить
: 
.9. Принять k=1.
10. Выбрать
аиз .11. Найти
аиз M2 такой, что 
, и - соответствующий ему 
аиз D.12. Если
=1, то 
, k=k+1 и перейти к п.10, иначе п.13;13. Принять i=1.
14. Если
, то перейти к п. 15, иначе - п.25.15. Если
аи 
аи 
, то перейти к п.16, иначе i=i+1 и - п.14.16. Для
авыполнить операцию 
аи сформировать 
:
, 
,
, 
,
, 
, 
.17. Вычислить
. Если 
, то перейти к п.18, иначе 
аи - п.14.18. Вычислить
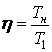. Если 
, то останов и выдача М1, иначе перейти к п.19.19. Принять
: 
.20. Принять Т0=Т1.
21. Принять
.22. Для
авыполнить операцию аи сформировать 
:
, 
,
, 
,
, 
, 
.23. Принять
: 
.24. Принять k=k+1 и перейти к п.26.
25.
, k=k+1.26. Если
, то останов и выдача М1, иначе перейти к п.9В третьей главе описаны программная модель разработанного алгоритма планирования размещения задач и результаты статистических исследований его эффективности.
Для моделирования и тестирования разработанного метода планирования размещения задач в кластерных системах была разработана на языке Си++ программная система, котораяа позволяет программно реализовать алгоритм размещения, строить графики изменения показателей эффективности
аи 
апри каждой пробной перестановке и с заданной точностью фиксировать время расчета.Целью исследования было определение величины выигрыша
ав снижении задержки в результате применения разработанного метода при разных видах и степенях заполнения МОИ, соответствующих широкому диапазону изменения степени связности между задачами пакета программ, запланированных к обработке в базовом матричном блоке. Результаты, соответствующие матрице наилучшего размещения 
, начальному и достигнутому отклонению задержки Т от Tinf: 
аи асоответственно, достигнутому выигрышу s в разах, а так же времени, затраченному на поиск, выводятся на экран.