Файл: Образовательная программа (направленность (профиль)) Автоматизация технологических процессов и производств в машиностроении.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.10.2023
Просмотров: 52
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рисунок 6 - Модель работающего гидравлического трансформатора автомобиля БЕЛАЗ выполненная в Ansys
Так же отдельно были выполнены расчеты пера лопатки турбинного колеса гидротрансформатора, так как при изучении натурных образцов, на предприятии изготовителя, на перьях лопаток колец турбинного и промежуточного, были обнаружены следы кавитационного разрешения и появление сети трещин. Однако, условия работы агрегата в целом, не могут быть причиной появления такого дефекта, Так же, при изучении конструкторской документации на предприятии изготовителе, были получены данные, о том, что замена рекомендуемого конструкционного материала не проводилась. Таким образом, изучение происходящих в процессе явлений так же является необходимым (Рисунок 7).
1
Например, на рисунке 1
В современных условиях машиностроительных предприятий, где наиболее приоритетными направлениями работы, в области повышения эффективности проведения изготовления или ремонта машин и механизмов является инженерный анализ. Инженерный анализ выполняется для отдельных узлов, деталей или механизма в целом.
Основными проблемами инженерного анализа, в особенностях при использовании его в условиях машиностроительных предприятий является учет большого количества физических процессов, неточность постановки задачи и различные подходы к формированию методики инженерного анализа вызывают, существенные проблемы при выборе как правильной методики, так и формированию конкретных результатов анализа.
В целях формирования определенной структуры методов анализа, нами было предложено разделить методы на определенные группы анализа:
1. Методы, подразумевающие определенные программные комплексы анализа;
2. Методы, использующие универсальные программные комплексы анализа;
3. Методы, использующие строго ориентированные комплексы анализа определенных узких проблем;
4. Методы, использующие анализ механизмом управления работой по подготовке всего комплекса производства.
Все методы являются, зачастую, программными продуктами, созданными для комплексного анализа всех процессов протекающих в анализируемом изделии. У каждой системы существуют свои технологии задания процессов, однако все описания процессов осуществляются с помощью наборов математических операторов, каким бы не был интерфейс задания параметров. Следовательно, исходя из выше сказанного, специалист осуществляющий инженерный анализ должен обладать широким спектром познаний как в области изучаемой темы так и в области математики и физики.
Так же в условиях большого количества различных методик анализа и соответственно программных систем, существуют сложности в системах взаимодействия между программами по созданию трехмерных моделей и их инженерным анализом. Особенно остро строит вопрос об анализе в области структурных данных о конструкции, линейного анализа выполненного на статическую устойчивость, анализ модов внутреннего резонанса, тепловые анализы, анализ конвекции.
Для решения задачи, поставленной в целях работы, необходимо провести анализ модов внутреннего резонанса, тепловой анализ, и общий инженерный анализ. Из существующих на сегодняшний момент программных комплексов наиболее полно подходят ряд систем:
1. ANSYS, Inc. (США);
2. SAMTECH (Бельгия);
3. MacNeal Schwendler Corporation (МSС) (США).
Зная цели исследования, и возможности предприятия, на котором будут собираться данные для анализа, необходимо провести анализ ступицы гидротрансформатора необходима программа использующие метод конечных элементов или (FEA). Следовательно, для решения определенной задачи необходим комплекс ANSYS, который позволяет оперировать не только методом конечных элементов, но и вносить условия для задаваемой методики анализа в виде математических операторов.
1.1 Основы метода конечных элементов как основной принцип современного инженерного анализа
Рассмотрим методику конечных элементов, которая базируется на методе математических матриц. То есть, вся поверхность тела, которое рассматривается, делится на большое количество полигонов, каждый из которых – можно описать уравнениями физики, математики в частных производных. Данным методом, возможно решать наиболее сложные аналитические задачи, такие как анализ механических, тепловых, гидростатических задач.
Необходимо
изучить этот метод анализа, так как он является основой всех автоматизированных методов проектирования и инженерного анализа (САПР).
Проанализируем метод конечных элементов, для понимания основ и задания верных параметров при проведении инженерного анализа конструкции. Для этого, изучим краткое описание применяемых уравнений и типов и видов конечных элементов, применяемых при использовании метода конечных элементов или МКЭ.
В специализированное литературе, многообразие методов описания конечных элементов с помощью математических формул можно разделить в несколько больших групп. Каждая группа описывает наиболее часто встречающийся тип элементов:
Уравнения, описывающие конечные элементы элептическими уравнениями:
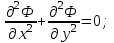
Уравнения, описывающие конечные элементы параболическими уравнениями:
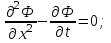
Уравнения, описывающие конечные элементы гиперболическими уравнениями:
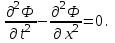
В условиях задач, решаемых в представленной работе, имеющий потенциальный тип, а так же при решении задач связанных с расчетом режимов в электростатике и магнитостатике при стационарных режимах работы, при определении режимов деформации тел, определении потоков возникающих в жидких и газообразных телах, теплотехнической физике. Наиболее часто с перечисленными уравнениями используют функции граничных условий:
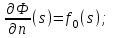
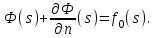
Решение задач по диффузному смешиванию, обязательно использование уравнений параболического типа. Так же обязательным, этот тип уравнений, является в решении задач электротехники. С этим типом уравнений обязательным является использование 2 типов граничных условий:
- обязательно выполнение условий Диркхле, Неймана;
-условие t=0.
Так же для анализа условий вибрации, вызванных механическими причинами и внутренним резонансом, и особенно анализ электромагнитных волн обязательно использование решений гиперболического типа.
Это уравнение может трансформироваться в уравнение эллиптического типа при периодическом возбуждении. Оно используется также для отыскания собственных мод вибрации твердых тел или мод электромагнитных волн [6].
Рассмотрим виды элементов, на которые возможно разделить тело для определения различных напряжений и усилий. Основные типы этих элементов изображены на рисунке 1.
Приведем краткую характеристику основных конечных элементов, используемых во всех CAD системах. Основным элементом, является фермовый конечный элемент (Рисунок 1а), наиболее полно используется при расчете и анализе пространственных конструкций выполненных по типу ферм и пространственных рам. Так же имеет особый тип использования в совокупности с другими элементами, может выступать в роли частичного закрепления конструкции в неподвижном основании.
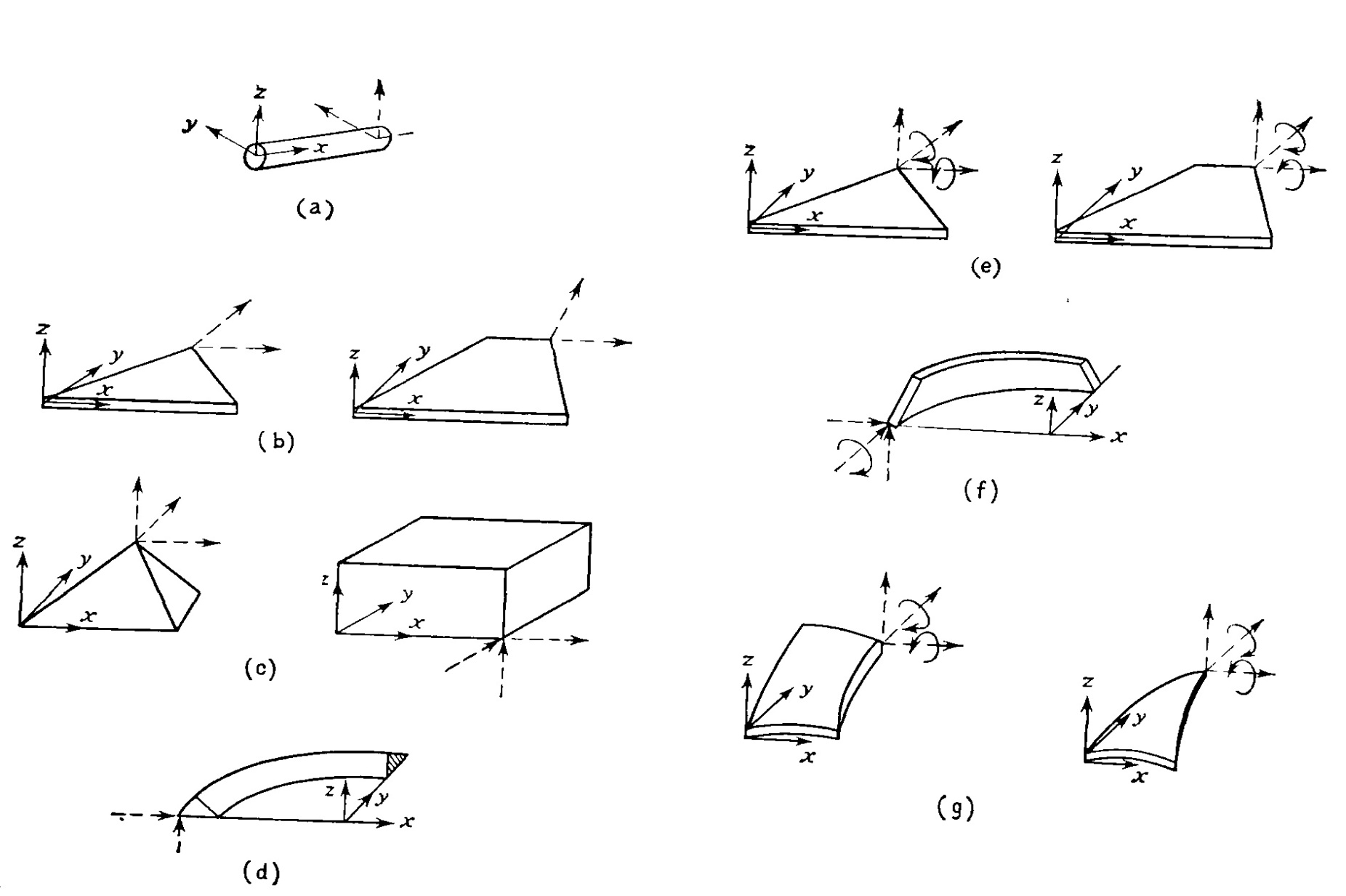
(а) стержневой (простой фермовой); (b) плоско-напряженный; (с) сплошные (трехмерные); (d) осесимметричный сплошной; (е) изгибаемый пластинчатый; (f) осесимметричный тонкостенный оболочечный; (g) искривленный тонкостенный оболочечный [4].
Рисунок 7 - Типы конечных элементов
Следующим по частоте использования при конечно-элементном моделировании является пластина, изображенная на рисунке 1b. Бывают пластины треугольные и четырех угольные, к подобному типу можно отнести и узко специализированные типы элементов. Подобный тип элементов является наиболее распространенным и большинство методик анализа, расчета строится именно на подобных типах элементов и достаточно хорошо изучены.
Следующим типом элементов являются трехмерные элементы, наиболее часто это тетраэдары и параллелипипеды. Применяются при моделировании строения грунтов, оценки воздействия последствий напряжений горного массива и оценки влияния радиоактивного излучения (Рисунок 4с). Следует так же обратить внимание, что подобные типы элементов используются повсеместно для CAD/CAE анализа и построений различных конструкций.
Одной из важнейших задач, решаемых с помощью метода конечных элементов это проектирование и анализ бетонных изделий, а так же анализ резервуаров. Иными словами, трехмерный анализ осесимметричных тел (рисунок 4d). Применяет совместно со всеми видами конечных элементов, так как в реальных условиях нагрузки или воздействия бывают приложены ассиметрично.
При анализе тонкостенных сооружений и конструкции используется тип конечных элементов, показанный на рисунке 4e. Так же используется при анализе плосконапряженных элементов.
Из наиболее новых элементов, используемых в последних версиях программ анализа, существуют элементы изображенные на рисунке 4f. В таком типе элементов происходит учет плоских тонких оболочек, теория плоских ассиметричных является промежуточной между теорией изгиба и растяжения тонкостенных элементов.
Преимуществами такого типа конечных элементов, является полный учет всех воздействий на поверхность анализируемого тела.
Для анализа поверхностей участвующих в сложных движениях используются элементы показанные на рисунке 4g. Данный тип объединяет в себе все выше перечисленные элементы и позволяет проводить расчеты сложных пространственных конструкции.
Следующим этапом рассмотрения анализа конструкций методом конечных элементов является понятия разбиения конструкции на конечные элементы и построение связи между ними, с помощью аппроксимации неизвестной функции.
Основной идей при использовании метода конечных элементов служит следующее определение конечного элемента. Подобным типом элементов, называют некую область обладающую несравнимо малую величину, по сравнению с общей конструкцией, но имеют конечный размер и подчиняются тем же физическим явлениям.
В большинстве случаев конечные элементы имеют вид треугольников или тетраэдоров. Так же каждый элемент характеризуется степенью аппроксимации неизвестной функции и степенью вовлеченности в общую конструкцию, иными словами геометрическими узлами. Степень аппроксимации может быть от 1 до 6.
На каждом конечном элементе определим аппроксимирующие функции
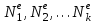таким образом, чтобы неизвестная функция была линейной комбинацией этих аппроксимирующих функций. Эти функции связаны с узлами элемента и служат его характеристикой [4].Для элементов сложной формы можно определить аппроксимирующие функции, называемые иногда функциями формы,которые получают посредством геометрических преобразований, начиная с некоторого стандартного элемента [4].
Основа метода конечных элементов состоит в определении способа разбиения области на подобласти (конечные элементы) без перекрытия и пересечения. На рисунках 2-4 приведено несколько примеров разбиения для плоских и объемных тел.
Когда разбиение будет осуществлено, исходная область Ω будет определяться сетью точек, являющихся общими узлами смежных элементов. Неизвестная функция после решения задачи будет характеризоваться ее значениями в каждом узле разбиения. Эта неизвестная функция будет интерполироваться в области