Добавлен: 24.10.2023
Просмотров: 43
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Автономная некоммерческая образовательная организация высшего образования «Сибирский институт бизнеса и информационных технологий»
КЕЙС
Дисциплина: Высшая математика
Выполнила студентка:
Cухоруков Ю.Е.
Город Омск
Омск 2022
ПРАКТИЧЕСКОЕ ЗАДАНИЕ №1. ЛИНЕЙНАЯ АЛГЕБРА
Задача 1. Модель межотраслевого баланса.
Втаблицеприведеныкоэффициентыпрямыхзатратиконечнаяпродукцияотраслейнаплановыйпериод,усл.ден.ед.
| Отрасль | Потребление | Конечныйпродукт | |||||
| Промышленность | Сельское хозяйство | ||||||
| Производство | Промышленность | a | b | t | |||
| Сельское хозяйство | c | d | f | ||||
Найти:
-
плановые объемы валовой продукции отраслей, межотраслевыепоставки,чистуюпродукцию отраслей; -
необходимый объем валового выпуска каждой отрасли, если конечноепотребление продукции сельского хозяйства увеличится на k%, апромышленностинаl%.
| Вариант | a | b | c | d | t | f | k | l |
| 13 | 0,4 | 0,25 | 0,5 | 0,4 | 300 | 200 | 30 | 40 |
РЕШЕНИЕ. Заполним таблицу данными варианта 13:
| Отрасль | Потребление | Конечный продукт | ||
| Промышленность | Сельское хозяйство | |||
| Производство | Промышленность | 0,4 | 0,25 | 300 |
| Сельское хозяйство | 0,5 | 0,4 | 200 | |
Найдем плановые объемы валовой продукции отраслей
 Х= Х= |  Х1 Х1 |
| Х2 |
Зная, что задана матрица

| А= | 0,4 |  0,25 0,25 |
| 0,5 | 0,4 |
прямых затрат и вектор конечного продукта
 Y= Y= |  300 300 |
| 200 |
Используем основную формулу межотраслевого баланса X (E A)1Y.
Обратная матрица к матрице

| E-A= |  0,6 0,6 | -0,25 |
| -0,5 | 0,6 |



Имеет вид Т
| (Е-А)-1= 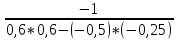 | 0,6 | -0,25 |  = = | 2,553 | 1,064 |
| -0,5 | 0,6 | 2,128 | 2,553 |

| Х =(Е-А)-1=Y= | 2,553 | 1,064 | 300 | = |  978,723 978,723 | |
 2,128 2,128 |  2,553 2,553 | 200 | 1148,936 | |
Таким образом, плановый объем валовой продукции отраслей равен
x1 978, 723 (промышленность), x2 1148, 936 (сельское хозяйство).
Найдем межотраслевые поставки. Коэффициент прямых затрат определяется как объём ресурса i, необходимый для производства единицы продукта j,
т.е. a
xij,
i, j 1, 2, 3. Отсюда можно найти x
a x
, i, j 1, 2, 3.

x
ij
j
ij ij j
Получаем:
x11 a11 x1 0, 4 978, 723 391, 489.
x21 a21 x1 0, 5 978, 723 489, 362.
x12 a12 x2 0, 25 1148, 936 287, 234.
x22 a22 x2 0, 4 1148, 936 459, 574.
Получаем таблицу:
| Отрасль | Потребление | Конечный продукт | ||
| Промышленность | Сельское хозяйство | |||
| Производство | Промышленность | 391,489 | 287,234 | 300 |
| Сельское хозяйство | 489,362 | 459,574 | 200 | |
Найдем условно чистую продукцию отраслей из формулы
xj x1 j x2 j zj, откуда
zj xj x1 j x2 j ,
j 1, 2 .
Получим:
z1 x1 x11 x21 97,872 ,
z2 x2 x12 x22 402,128




Найдем необходимый объем валового выпуска каждой отрасли, если конечное потребление продукции сельского хозяйства увеличится на 30%, а промышленности на 40%, то есть новый вектор конечной продукции примет вид:
300 1, 3 390
Y' .
200 1, 4 280

Тогда валовой выпуск будет равен:





X' (E A)1Y' 2, 553 1, 064 390 1293, 617 .
2,128 2, 553 280 1544, 681
Новый валовой выпуск для промышленности: 1293,617, для сельского хозяйства: 1544,681.
Решение
Для разложения вектора по базису запишем векторное уравнение: x 1 ⋅ p1 + x 2 ⋅ q 2 + x 3 ⋅ r 3 = х x1⋅p1+x2⋅q2+x3⋅r3=x Найдем определитель матрицы.
Так как определитель матрицы не равен нулю, то введённая система векторов является базисом. △ = 29 △=29

Показать подробное решение. Решим уравнение методом Гаусса:
| 1 | 0 | 0 | -3 |
| 0 | 1 | 0 |  2 |
| 0 | 0 | 1 | 0 |
Подставим значения из решения системы Гаусса в векторное уравнение x = − 3 a1 + 2 ⋅ a2 + 0 ⋅a3
Ответ:
x = −3a1 + 2a2 + 0a3
Задание 3
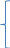
2х1+3х2-2х3+х4=0
х1+х2+3х3-5х4=0
-3х1-5х22+7х3-7х4=0
Решение
Выпишем основную матрицу системы:
| |
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (-1). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой:
| |
Умножим 2-ую строку на (3). Добавим 3-ую строку к 2-ой:
| |
Умножим 1-ую строку на (-2). Добавим 2-ую строку к 1-ой:
| |
Найдем ранг матрицы.
| |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 3.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2,x3, значит, неизвестные x1,x2,x3 – зависимые (базисные), а x4 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
| |
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
- 2x2 + 16x3 = 9x4
- 3x1 - 5x2 + 7x3 = - 6x4
Методом исключения неизвестных находим нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x1,x2,x3 через свободные x4, то есть нашли общее решение:
x3 = - 13x4
x2 = - 9/2x4
x1 = 19/2x4
