Файл: Проверка гипотезы о законе распределения генеральной.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 24

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Вариант 21


xi, xi1

[0;3)
[3;6)
[6;9)
[9;12)
[12;15)
[15;18)
[18;21)
[21;24)

ni
38
20
10
9
8
7
5
3

«Проверка гипотезы о законе распределения генеральной совокупности по критерию Пирсона»

Получены результаты (сгруппированные по интервалам) статистического обследования длительности 100 ремонтных операций, производимых мастерскими:

xi, xi1

[0;3)
[3;6)
[6;9)
[9;12)
[12;15)
[15;18)
[18;21)
[21;24)

ni
38
20
10
9
8
7
5
3

Требуется :

  1. Построить гистограмму частностей;

  2. Найти числовые характеристики выборки (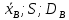 ; 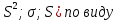гистораммы и замечаниям числовых характеристик выдвинуть гипотезу о законе распределения случайной величины X- длительности ремонтных операций, оценить параметры теоретического закона и записать его вид;

  3. Проверить выдвинутую гипотезу о законе распределения X по критерию Пирсона ( уровень значимости выбрать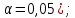

  4. Проверить две альтернативных гипотезы о законе распределения X по критерию Пирсона.

РЕШЕНИЕ:

  1. Для построения гистограммы строим вспомогательную таблицу :

Расчетная таблица для построения гистограммы частостей
Разряды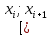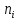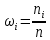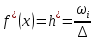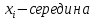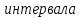










1
[0;3)
38
0,38
0,127
1,5

2
[3;6)
20
0,20
0,067
1,5

3
[6;9)
10
0,10
0,033
7,5

4
[9;12)
9
0,09
0,030
10,5

5
[12;15)
8
0,08
0,027
13,5

6
[15;18)
7
0,07
0,023
16,5

7
[18;21)
5
0,05
0,017
19,5

8
[21;24)
3
0,03
0,010
22,5

Контроль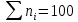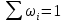













По данным таблицы построим гистограмму частостей ( рис. 1)



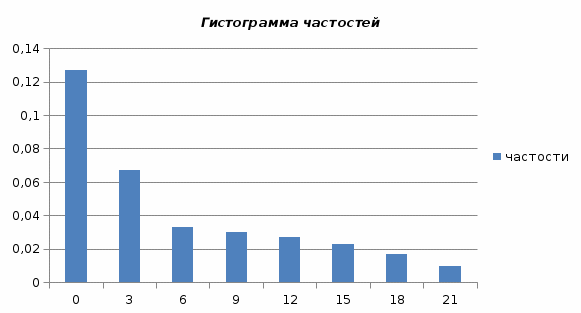
Рис. Гистограмма частостей


  1. Находим числовые характеристики выборки:



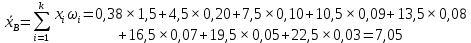
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).



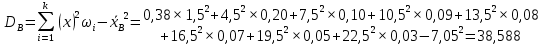
Среднее квадратическое отклонение.



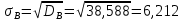
Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).





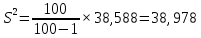
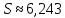
Каждое значение ряда отличается от среднего значения 7.05 в среднем на 6.212
Оценка среднеквадратического отклонения.



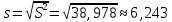
  1. Учитывая вид гистограммы и близость статистического среднего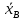 и выборочного среднего 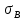по своим значениям , выдвигаем основную гипотезу в пользу показательного закона распределения, функция плотности которого имеет вид:





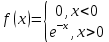
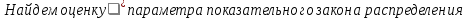
Выборочное среднее 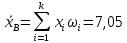несмещенная и состоятельная оценка математического ожидания.

Используя метод моментов , имеем

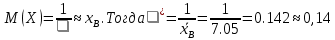
Заменяя

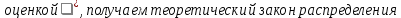
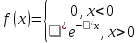т.е

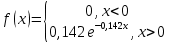
  1. В качестве меры расхождения между статистическим и гипотетическим (теоретическим) распределениями возьмем критерий Пирсона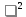

Мера расхождения в этом критерии определяется равенством

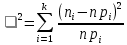
Где n –объем выборки ( у нас n=100) ;


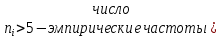
Элементов в i- м интервале); k-число интервалов ( у нас k=8);

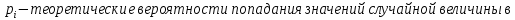
В рассмотренном эмпирическом распределении имеются частоты меньше 5. При использовании критерия Пирсона такие интервалы целесообразно объединить с соседними. После объединения интервалов с низкой степенью частоты получим интервальный ряд:

xi, xi1

[0;3)
[3;6)
[6;9)
[9;12)
[12;15)
[15;18)
[18;24)

ni
38
20
10
9
8
7
8

Находим теоретические вероятности



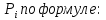
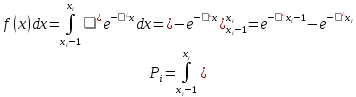
Где

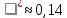
Для нахождения вероятностей воспользуемся данными таблицы ( приложение 6)















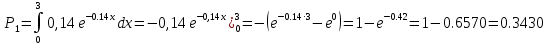
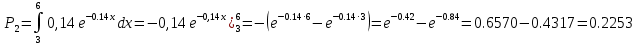
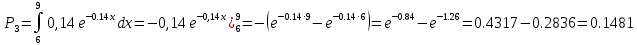
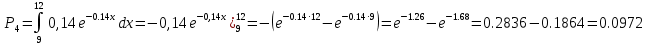
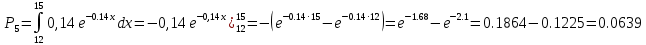
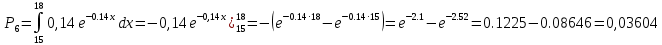
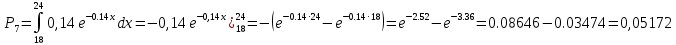
Дальше вычисления, необходимые для определения расчетного значения выборочной статистики

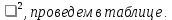
Расчетная таблица для проверки гипотезы о показательном законе распределения генеральной совокупности

xi, xi1

[0;3)
[3;6)
[6;9)
[9;12)
[12;15)
[15;18)
[18;24)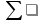


ni
38
20
10
9
8
7
8
100



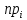34
23
15
10
7
4
5
98



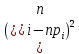16
9
25
1
1
9
16
-





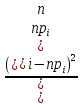0.47
0.39
1.67
0.1
0.14
2.25
3.2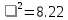


Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=1 (параметр λ).
Kkp(5,0.05) = 11.1; Kнабл = 8.22
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют показательный закон.

  1. Проверим альтернативную гипотезу о распределении генеральной совокупности по нормальному закону, функция плотности которого имеет вид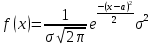

  2. Находим теоретические вероятности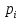 по формуле



















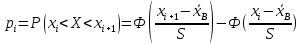
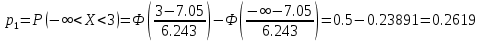
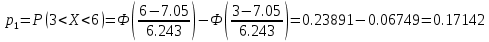
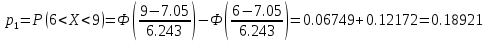
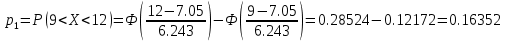
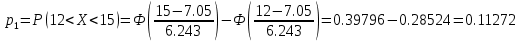
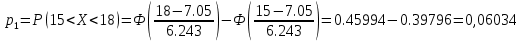
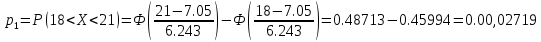
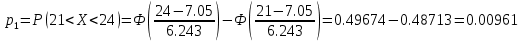
Все вычисления , необходимые для определения расчетного значения занесем в таблицу

xi, xi1

[0;3)
[3;6)
[6;9)
[9;12)
[12;15)
[15;18)
[18;24)


ni
38
20
10
9
8
7
8
100



26
17
19
16
11
6
3
98



144
9
81
49
9
1
25
-





5,5
0,53
4,3
3,1
0,82
2.25
0,17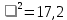

Смотрите также файлы