Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение K_набл, тем сильнее довод против основной гипотезы.Поэтому критическая область для этой статистики всегда правосторонняя: [K_kp;+∞).Её границу K_kp = χ²(k-r-1;α) находим по таблицам распределения χ² и заданным значениям s, k (число интервалов), r=1 (параметр λ).Kkp(6,0.05) = 12,6; Kнабл = 17,2
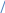
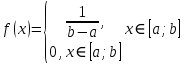
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл Kkp, поэтому есть оснований отвергать альтернативную гипотезу гипотезу. 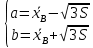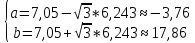предположение о том, что данные выборки имеют нормальный закон отвергается.Проверим альтернативную гипотезу о распределении генеральной совокупности по равномерному закону , функция плотности которого имеет вид:Оценим по выборке параметры а и в равномерного закона распределения по методу моментов Тогда Заменим a и b найденными оценками , получаем вид теоретического закона распределения f(x)=0.046Находим теоретические вероятности : 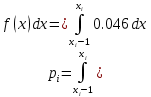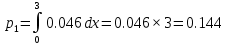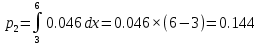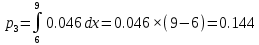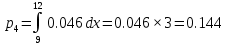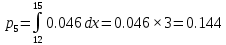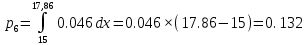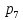Все вычисления необходимые для определения расчетного значения выборочной статистики χ²

xi, xi1 	[0;3)	[3;6)	[6;9)	[9;12)	[12;15)	[15;24)
ni	38	20	10	9	8	15	100
	14,4	14,4	14,4	14,4	14,4	13,2	85,2
	556,96	31,36	19,36	29,16	40,96	37,24	-

---

Смотрите также файлы

• Первая помощь при ожогах и отморожениях.docx

• Темы эссе Преимущества использования исуп.docx

• У больного с приступами удушья при проведении пикфлоуметрии выявлена положительная проба с бронхолитиком (прирост 30%).docx

• Программа среднего профессионального образования Право и организация социального обеспечения соо дисциплина Английский язык. Практическое задание 2.docx

• 9шоцваысш0щзльуцкавыс0чшщзльдукцавысш0щлзьдцукуавысшщлзьдуцкавышщлзь0ш.docx