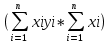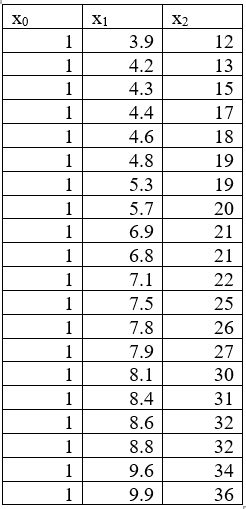
По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов x₁ (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих x₂ (%).

Требуется:

1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.

2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.

3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации .

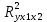5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора x₁ после x₂ и фактора x₂ после x₁.

6. Составить уравнение линейной парной регрессии, оставив лишь значащий фактор.

Номер предприятия	y	x1	x2	Номер предприятия	y	x1	x2
1	7	3.9	12	11	11	7.1	22
2	7	4.2	13	12	12	7.5	25
3	7	4.3	15	13	13	7.8	26
4	7	4.4	17	14	12	7.9	27
5	8	4.6	18	15	13	8.1	30
6	8	4.8	19	16	13	8.4	31
7	9	5.3	19	17	13	8.6	32
8	9	5.7	20	18	14	8.8	32
9	10	6.9	21	19	14	9.6	34
10	10	6.8	21	20	14	9.9	36

---

Рассчитаем сначала парные коэффициенты корреляции по формуле



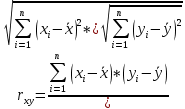
Получим:

ryx1	ryx2	rx1x2
0.983	0.963	0.970

Связь между факторной переменной и результативной сильная. Также наблюдается сильная связь между факторными переменными.

Они указывают на весьма сильную связь каждого фактора с результатом, а также высокую межфакторную зависимость.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.

Коэффициент множественной детерминации можно определить через матрицы парных коэффициентов корреляции:



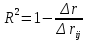
Находим определитель матрицы парных коэффициентов корреляции:

∆r
1	0.983	0.963
0.983	1	0.970
0.963	0.970	1
0.001908007

определитель матрицы межфакторной корреляции:

∆rij
1	0.970
0.970	1
	0.058653

Коэффициент множественной детерминации:

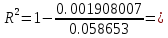0.967469445

Коэффициент множественной детерминации указывает на весьма сильную связь всего набора факторов с результатом.

Коэффициент множественной детерминации

---

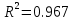
оценивает долю дисперсии результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 96,7% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.

Оценку надежности уравнения регрессии в целом и показателя тесноты связи дает F-критерий Фишера:

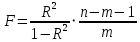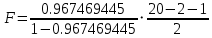= = 252.7928071

В нашем случае фактическое значение F-критерия Фишера = 255,8

Получили, что F_факт=255 > F_табл=3,59 (при n = 20), т.е. вероятность случайно получить такое значение F-критерия не превышает допустимый уровень значимости 5%. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения.

Вычислим коэффициенты множественной регрессии матричной формулой системы уравнений метода наименьших квадратов:

b = ((X^TX)^-1)*(X^TY)

матрица X



Матрица X^T



Получим

b = ((XTX)-1)*(XTY)
b0	1.554
b1	1.130
b2	0.059

Таким образом, получили следующее уравнение множественной регрессии:



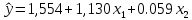
Уравнение регрессии показывает, что при увеличении ввода в действие основных фондов на 1 (при неизменном уровне удельного веса рабочих высокой квалификации) выработка продукции на одного рабочего увеличивается в среднем на 1.130 тыс. руб., а при увеличении удельного веса рабочих высокой квалификации в общей численности рабочих на 1% (при неизменном уровне ввода в действие новых основных фондов) выработка продукции на одного рабочего увеличивается в среднем на 0.059 тыс. руб.

---

Вычислим частный критерий Фишера

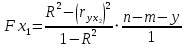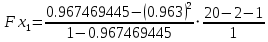= = 20,92

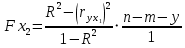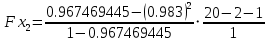= = 0,80

F_крит = 4,45

Получили, что Fx₂ = 0.80 < F_крит = 4.45 < Fx₁ = 21

Следовательно, включение в модель фактора x₂после того, как в модель включён фактор х₁ статистически нецелесообразно: прирост факторной дисперсии за счёт дополнительного признака х₂ оказывается незначительным, несущественным; фактор х₂ включать в уравнение после фактора х₁ не следует.

Получить влияние одного фактора и исключить воздействие остальных (элиминирование).

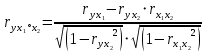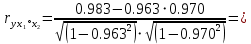= 0.743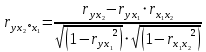

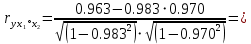= 0.212

Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.

Оценка параметров уравнения регрессии в стандартизованном масштабе

Коэффициенты β₁ и β₂ стандартизованного уравнения регрессии 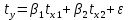  находятся по формуле:

β_j

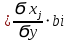
Ϭy	2.58
Ϭx1	1.89
Ϭx2	7.02

β₁ 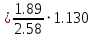= 0.826231

β₂

---

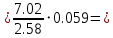
0.161397

Т.е. стандартизованное уравнение будет выглядеть следующим образом:

.

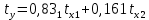Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что ввод в действие новых основных фондов оказывает большее влияние на выработку продукции, чем удельный вес рабочих высокой квалификации.

Оценка параметров уравнения регрессии в стандартизованном масштабе

β_j

Коэффициент эластичности показывает, на сколько процентов изменится в среднем результативная переменная, если факторная переменная изменится на 1%.







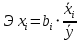
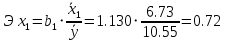
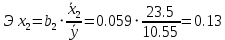
Т.е. увеличение только основных фондов (от своего среднего значения) или только удельного веса рабочих высокой квалификации на 1% увеличивает в среднем выработку продукции на 0,72% или 0,13% соответственно. Таким образом, подтверждается большее влияние на результат у фактора х₁, чем фактора х₂.

Общий вывод состоит в том, что множественная модель с факторами х₁ и х₂ содержит неинформативный фактор х₂ , то можно ограничиться уравнением парной регрессии вида:



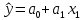
Найдём его параметры:





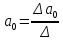
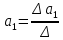
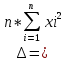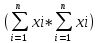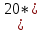) - = 976.98) -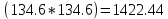

-

---

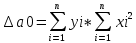Смотрите также файлы

• Основы банковского дела Тема Роль и функции банков.pdf

• Международный менеджмент индустрии гостеприимства.docx

• Программа среднего профессионального образования 44. 02. 03 Педагогика дополнительного образования (в области социальнопедагогической деятельности) Дисциплина Физическая культура Практическое задание 6.doc

• Тема Прокурорский надзор за исполнением законов судебными приставами и за исполнением наказаний и иных мер принуждения.docx

• Дыхательная гимнастика.pptx