Введение

Криптография – специальная система изменения обычного письма, используемая с целью сделать текст понятным лишь для ограниченного числа лиц, знающих эту систему.

Криптография – наука о защите информации с использованием математических методов.

Современная криптография включает в себя:

• 
  симметричные криптосистемы;
  
• 
  асимметричные криптосистемы;
  
• 
  системы электронной цифровой подписи (ЭЦП);
  
• 
  хеш-функции;
  
• 
  управление ключами;
  
• 
  получение скрытой информации;
  
• 
  квантовая криптография.
  

Симметричное шифрование - симметричными называются алгоритмы, в которых для шифрования и дешифрования используется один и тот же (известный только отправителю и получателю) секретный ключ.

Асимметричные криптоалгоритмы призваны в первую очередь устранить основной недостаток симметричных криптосистем – сложность управления и распространения ключей.

Основой всех асимметричных криптоалгоритмов является большая вычислительная сложность восстановления открытого текста без знания закрытого ключа.
Основная часть

Алгоритм RSA (буквенная аббревиатура от фамилий Rivest, Shamir и Adleman) – криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел. Криптосистема RSA стала первой системой, пригодной и для шифрования, и для цифровой подписи.

1. 
   История создания
   

Трое учёных Рональд Ривест (англ. Ronald Linn Rivest), Ади Шамир (англ. Adi Shamir) и Леонард Адлеман (англ. Leonard Adleman) из Массачусетского Технологического Института (MIT) приступили к поискам математической функции, которая бы позволяла реализовать сформулированную Уитфилдом Диффи и Мартином Хеллманом модель криптографической системы с открытым ключом. После работы над более чем 40 возможными вариантами, им удалось найти алгоритм, основанный на различии в том, насколько легко находить большие простые числа и насколько сложно раскладывать на множители произведение двух больших простых чисел, получивший впоследствии название RSA. Система была названа по первым буквам фамилий её создателей.

---

2. 
   Описание алгоритма
   

Первым этапом любого асимметричного алгоритма является создание пары ключей – открытого и закрытого и распространение открытого ключа "по всему миру".

1. 
   Создание ключей
   

Для алгоритма RSA этап создания ключей состоит из следующих операций:

1. 
   Выбираются два очень больших простых числа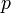   and  .
   
2. 
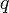   Вычисляется их произведение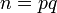  , которое называется модулем.
   
3. 
   Вычисляется значение функции Эйлера от числа  :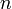
   

4. 
   Выбирается произвольное число   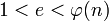(  ), взаимно простое со значением функции  .
   

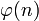Число   называется открытой экспонентой

5. 
   С помощью алгоритма Евклида вычисляется число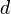  , которое удовлетворяет условию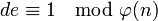 
   
6. 
   Пара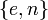   публикуется в качестве открытого ключа RSA.
   
7. 
   Пара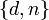   играет роль закрытого ключа RSA и держится в секрете.
   

2. 
   Шифрование и расшифрование
   

Предположим, отправитель хочет послать получателю сообщение 

---

.

Сообщениями являются целые числа в интервале от 0 до  , т.е .  . На рисунке 1 представлена схема алгоритма RSA.



Рисунок 1 – Схема алгоритма RSA

Алгоритм Отправителя:

1. 
   Взять открытый ключ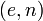   получателя
   

8. 
   Взять открытый текст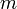 
   
9. 
   Зашифровать сообщение с использованием открытого ключа получателя:
   

Алгоритм Получателя:

1. 
   Принять зашифрованное сообщение 
   

10. 
    Взять свой закрытый ключ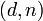 
    
11. 
    Применить закрытый ключ для расшифрования сообщения:
    

Уравнения (1) и (2), на которых основана схема RSA, определяют взаимно обратные преобразования множества   [5].

3. 
   Пример использования
   

В таблице 1 представлен пример использования алгоритма RSA. Отправитель отправил зашифрованное сообщение «111111» и получатель, используя свой закрытый ключ, расшифровал его.

Таблица 1 – Поэтапное выполнение алгоритма RSA

Этап	Описание операции	Результат операции
Генерация ключей	Выбрать два простых числа
	Вычислить модуль
	Вычислить функцию Эйлера
	Выбрать открытую экспоненту
	Вычислить секретную экспоненту
	Опубликовать ''открытый ключ''
	Сохранить ''закрытый ключ''
Шифрование	Выбрать текст для зашифровки
	Вычислить шифротекст
Расшифрование	Вычислить исходное сообщение

---

Заключение

В данном реферате был подробно рассмотрен алгоритм ассиметричного шифрования RSA. Была описана история его создания, описаны алгоритмы создания ключей, шифрования и расшифровки. Также представлен пример практического использования алгоритма RSA.

---

Смотрите также файлы

• Р. М. Каменева Практическая работа 1 Тема Особенности содержания обновленных фгос ооо, фгос соо.docx

• Введение Производственная практика по пм. 05 Выполнение работ по одной или нескольким профессиям рабочих, должностям служащих проходила в ооо Бутурлинское жкх с 21 июня 2023 года по 27июня 2023 года, которое расположено в р п..docx

• Профессиональные компетенции (код).doc

• Спектроскопия ямр на ядрах 19f слайд 2.docx

• 1. There is a village near the station. Is there a village near the station.docx