Задача 1.



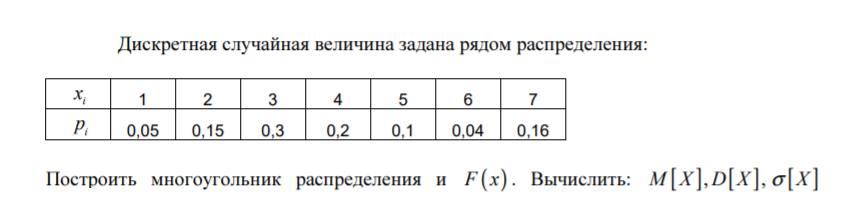
Решение





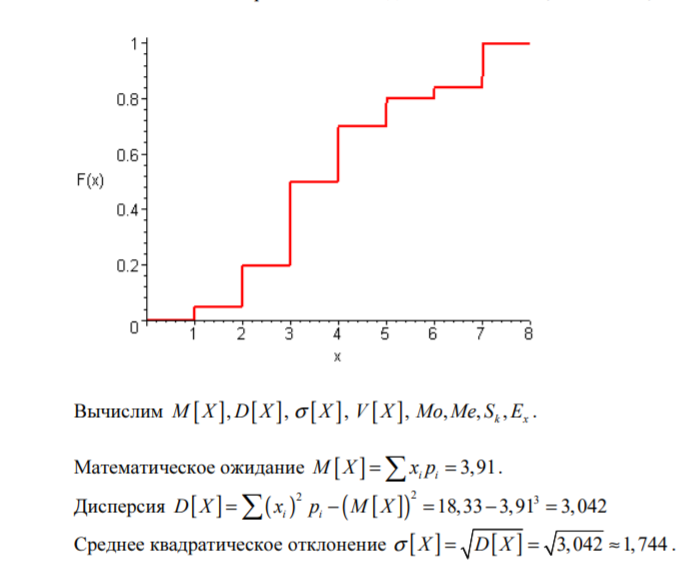
Задача 2.

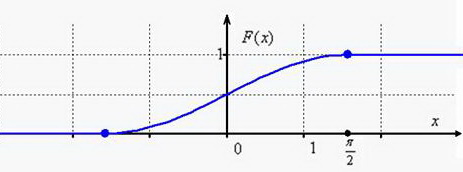
Непрерывная случайная величина   задана функцией распределения вероятностей (в вашем случае ее надо записать. Подсказка: вспомните, например, как строить прямую по двум точкам. Смотрите контрольную работу №1):


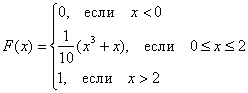
Вычислить  , построим ещё графики   и  .

Решение.

Начнём с графика функции распределения. Функция задана кусочно. Кубическую параболу, например, можно построить с помощью дополнительных точек:

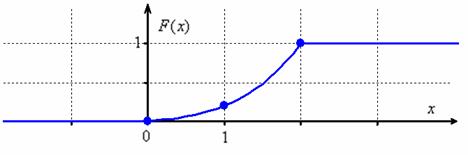
Найдем функцию плотности распределения вероятностей:


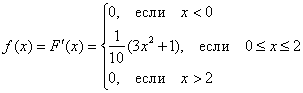
И снова опорные точки:   с чертежом:

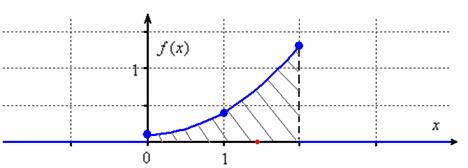
Проверим, что найденная нами функция – функция плотности ( )

 – данный результат равен заштрихованной площадии с вероятностной точки зрения означает тот факт, что случайная величина 

---

достоверно примет одно из значений отрезка  .

Вычислим:
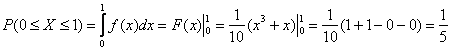 – вероятность того, что случайная величина   примет значение из промежутка 

Математическое ожидание:


 

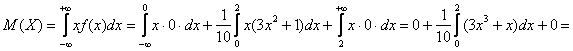
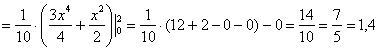
Дисперсию вычислим по формуле:


Сначала удобно разобраться с интегралом:


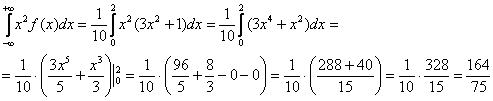
Таким образом:


И, наконец, среднее квадратическое отклонение:


Ответ: 

Задача 3.

Непрерывная случайная величина   задана функцией плотности распределения:


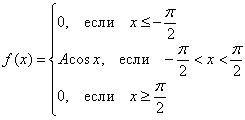
Найти значение   и составить функцию распределения вероятностей. Вычислить  . Построить графики  .

Решение.

Найдём константу 

---

. Используем свойство  . В данном случае:

На практике нулевые интегралы можно опускать, а константу сразу выносить за знак интеграла:

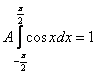
Пользуясь четностью подынтегральной функции вычислим:
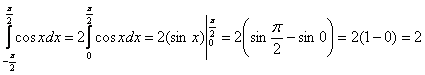 и подставим результат в уравнение:
, откуда выразим 

Таким образом, функция плотности распределения:


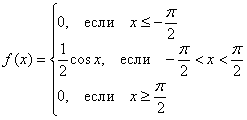
Функция распределения вероятностей – есть интеграл:


Так как наша   состоит из трёх кусков, то решение разобьётся на 3 шага:

1) На промежутке  , поэтому:


2) На интервале  , и мы прицепляем следующий вагончик:

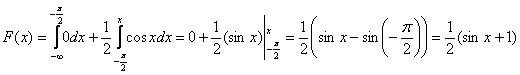
3) И, наконец, на  , и детский паровозик отправляется в путь:


Запишем получившуюся функцию распределения:


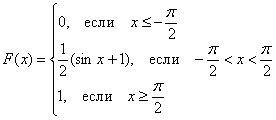
Найдем вероятность, 1 способ:

---

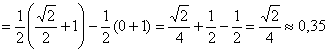 – вероятность того, что случайная величина   примет значение из промежутка 

2 способ:
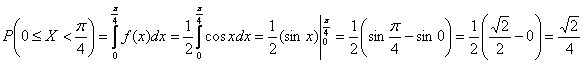, Выполним чертежи. График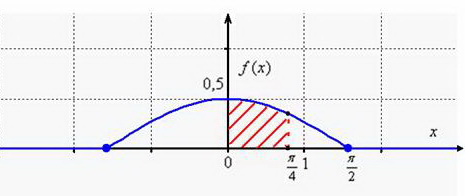   представляет собой график косинуса, сжатого вдоль оси ординат в 2 раза:

Осталось изобразить функцию распределения. График   представляет собой сжатуюв 2 раза вдоль оси ординат ОУ  синусоиду, сдвинутую на   вверх:

---

Смотрите также файлы

• Правила выполнения контрольных работ по учебной дисциплине теория вероятностей и математическая статистика ( Б. 6) для направления.docx

• 1. Таймменеджмент в современных условиях понятие, историческое развитие, сущность и содержание Задание Прочитайте одну из предложенных Вам ниже статей, опубликованных в современных научных журналах. Составьте краткий анализ прочитанного (на примере 1 стат.docx

• Применение vrтехнологий в области охраны труда производственное обучение, стажировка, инструктаж.docx

• Практическая работа арм кадры.docx

• Выполнение практических заданий по дисциплине профессиональная этика.docx