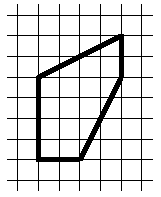
Муниципальный этап олимпиады школьников по математике, 6 класс, 2020-2021 уч. г.Максимальный балл – 31 балл1. Разрежьте изображённый на рисунке пятиугольник на две одинаковые (совпадающие при наложении) части. (5 баллов)2. Пять спортсменов: футболист, велосипедист, пловец, гимнаст и боксёр, из разных стран: Германии, Франции, Италии, Украины и России встретились на Олимпийских играх.Спортсмены из Франции и Украины никогда не играли в футбол. Спортсмены из Германии и Украины не любят ездить на велосипеде. Француз и немец обменялись адресами с гимнастом. Немец и итальянец посетили выступления пловца и футболиста. Велосипедист не француз.Определите, какой спортсмен из какой страны. (6 баллов)3. В ряд выписано 12 девяток 999999999999. Поставьте между ними знаки:+ , - , : , ^. , скобки, так чтобы получилось 2014 – год Олимпийских игр в Сочи. (6 баллов)4. Три купчихи - Сосипатра Титовна, Олимпиада Карповна и Поликсена Уваровна - сели пить чай. Олимпиада Карповна и Сосипатра Титовна выпили вдвоём 11 чашек, Поликсена Уваровна и Олимпиада Карповна - 15, а Сосипатра Титовна и Поликсена Уваровна - 14. Сколько чашек чая выпили все три купчихи вместе? (7 баллов)5. Шесть девочек взяли напрокат двухместную лодку. Сколько времени потребуется девочкам, чтобы всем покататься друг с другом, если каждая пара будет кататься по 15 минут? (7 баллов)Муниципальный этап олимпиады школьников по математике, 6 класс, 2020-2021 уч. г.Максимальный балл – 31 балл1. Разрежьте изображённый на рисунке пятиугольник на две одинаковые (совпадающие при наложении) части. 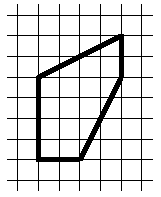(5 баллов)2. Пять спортсменов: футболист, велосипедист, пловец, гимнаст и боксёр, из разных стран: Германии, Франции, Италии, Украины и России встретились на Олимпийских играх.

---

Спортсмены из Франции и Украины никогда не играли в футбол. Спортсмены из Германии и Украины не любят ездить на велосипеде. Француз и немец обменялись адресами с гимнастом. Немец и итальянец посетили выступления пловца и футболиста. Велосипедист не француз.Определите, какой спортсмен из какой страны. (6 баллов)3. В ряд выписано 12 девяток 999999999999. Поставьте между ними знаки:+ , - , : , ^. , скобки, так чтобы получилось 2014 – год Олимпийских игр в Сочи. (6 баллов)4. Три купчихи - Сосипатра Титовна, Олимпиада Карповна и Поликсена Уваровна - сели пить чай. Олимпиада Карповна и Сосипатра Титовна выпили вдвоём 11 чашек, Поликсена Уваровна и Олимпиада Карповна - 15, а Сосипатра Титовна и Поликсена Уваровна - 14. Сколько чашек чая выпили все три купчихи вместе? (7 баллов)5. Шесть девочек взяли напрокат двухместную лодку. Сколько времени потребуется девочкам, чтобы всем покататься друг с другом, если каждая пара будет кататься по 15 минут? (7 баллов)Муниципальный этап олимпиады школьников по математике, 6 класс, 2020-2021 уч. г. (решения, ответы, критерии оценивания):1. Разрежьте изображённый на рисунке пятиугольник на две одинаковые (совпадающие при наложении) части. (5 баллов)

Ответ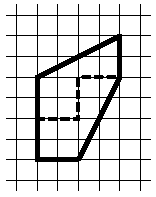

2. Пять спортсменов: футболист, велосипедист, пловец, гимнаст и боксёр, из разных стран: Германии, Франции, Италии, Украины и России встретились на Олимпийских играх.Спортсмены из Франции и Украины никогда не играли в футбол. Спортсмены из Германии и Украины не любят ездить на велосипеде. Француз и немец обменялись адресами с гимнастом. Немец и итальянец посетили выступления пловца и футболиста. Велосипедист не француз.Определите, какой спортсмен из какой страны. (6 баллов)Решение: решим задачу с помощью таблицы.

	футболист	велосипедист	пловец	гимнаст	боксёр
Германия	-	-	-	-	+
Франция	-	-	+	-	-
Италия	-	+	-	-	-
Украина	-	-	-	+	-
Россия	+	-	-	-	-

---

Ответ: футболист из России, велосипедист из Италии, пловец из Франции, гимнаст из Украины, боксёр из Германии.Основные принципы оценивания приведены в таблице.

Баллы	Правильность (ошибочность) решения
6	Полное верное решение.
5-6	Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
4-5	Решение содержит незначительные ошибки, пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений или дополнений.
4	Верно рассмотрен один из двух (более сложный) существенных случаев.
2-3	Доказаны вспомогательные утверждения, помогающие в решении задачи.
1	Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).
0	Решение неверное, продвижения отсутствуют.

3. В ряд выписано 12 девяток 999999999999. Поставьте между ними знаки:+ , - , : , ^. , скобки, так чтобы получилось 2014 – год Олимпийских игр в Сочи. (6 баллов)Решение: возможны варианты:а) 999 + 999 + 9 + 9 - 9 : 9 - 9 : 9 .Основные принципы оценивания приведены в таблице.

Баллы	Правильность (ошибочность) решения
6	Полное верное решение.
5-6	Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
4-5	Решение содержит незначительные ошибки, пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений или дополнений.
4	Верно рассмотрен один из двух (более сложный) существенных случаев.
2-3	Доказаны вспомогательные утверждения, помогающие в решении задачи.
1	Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).
0	Решение неверное, продвижения отсутствуют.

---

4. Три купчихи - Сосипатра Титовна, Олимпиада Карповна и Поликсена Уваровна - сели пить чай. Олимпиада Карповна и Сосипатра Титовна выпили вдвоём 11 чашек, Поликсена Уваровна и Олимпиада Карповна - 15, а Сосипатра Титовна и Поликсена Уваровна - 14. Сколько чашек чая выпили все три купчихи вместе? (7 баллов)Ответ: 20 чашекРешение: СТ+ОК=11 - по условию задачи ПУ+ОК=15 - по условию задачи СТ+ПУ+2ОК=26,СТ+ПУ=14- по условию задачи14+2ОК=262ОК=12ОК=6СТ=5ПУ=9ОК+СТ+ПУ=20Основные принципы оценивания приведены в таблице.

Баллы	Правильность (ошибочность) решения
7	Полное верное решение.
6-7	Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
5-6	Решение содержит незначительные ошибки, пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений или дополнений.
4	Верно рассмотрен один из двух (более сложный) существенных случаев.
2-3	Доказаны вспомогательные утверждения, помогающие в решении задачи.
1	Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).
0	Решение неверное, продвижения отсутствуют.

5. Шесть девочек взяли напрокат двухместную лодку. Сколько времени потребуется девочкам, чтобы всем покататься друг с другом, если каждая пара будет кататься по 15 минут? (7 баллов).Ответ: 225 мин.Решение: Найдем, сколько разных пар могут образовать 6 девочек. Для этого нужно, чтобы каждая из 6 девочек могла покататься с каждой из оставшихся 5 девочек:(6 * 5)/2 = 15 (пар).Каждой паре нужно 15 минут времени:15 * 15 = 225 (мин)Основные принципы оценивания приведены в таблице.

Баллы	Правильность (ошибочность) решения
7	Полное верное решение.
6-7	Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
5-6	Решение содержит незначительные ошибки, пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений или дополнений.
4	Верно рассмотрен один из двух (более сложный) существенных случаев.
2-3	Доказаны вспомогательные утверждения, помогающие в решении задачи.
1	Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).
0	Решение неверное, продвижения отсутствуют.

---

Смотрите также файлы

• Словарные диктанты.docx

• Технологии эффективного найма.docx

• Учебный курс Учебный модуль.pdf

• Работа классного руководителя в рамках реализации фгос.docx

• Мир во второй половине xx ввека содержание.docx