САНКТ-ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ

им. проф. М.А. БОНЧ-БРУЕВИЧА
ФАКУЛЬТЕТ ВЕЧЕРНЕГО И ЗАОЧНОГО ОБУЧЕНИЯ

Контрольная работа

по курсу

МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ В ИНФОКОММУНИКАЦИЯХ
Факультет _______

Группа _______

Студент ______________________

№ зач. кн. _______

Вариант 00

Проверил


г. Санкт-Петербург

2021 г.
КОНТРОЛЬНАЯ РАБОТА
Вариант 00
Задача 1. ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ

[1, с. 6-15, 60-83]; [2, с. 5-13, 35-53]

При неизменных условиях проведен ряд независимых измерений напряжения.

№	1	2	3	4	5
U, мB	2590	2606	2632	2598	2625

Предполагая, что случайная погрешность имеет нормальный закон распределения, оценить:

− среднее значение измеряемого напряжения;

− среднюю квадратическую погрешность однократного измерения;

− среднюю квадратическую погрешность результата измерения;

− доверительный интервал погрешности результата измерения при доверительной вероятности 0,90.

Ввести поправку на известную систематическую погрешность, равную - (минус) 29 мВ, и записать, соблюдая правила, результат измерения вместе с доверительным интервалом.

Решение:

Определим среднее значение напряжения по формуле





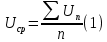
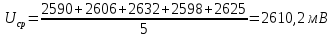
Найдем отклонения случайной величины от среднего значения:











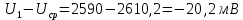
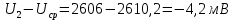
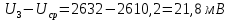
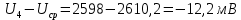
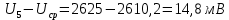
Найдем сумму отклонений:



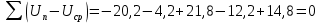
Сумма

---

отклонения равна нулю, следовательно, среднее значение вычислено верно.

Среднюю квадратическую погрешность однократного измерения (среднеквадратичное отклонение погрешности результата наблюдений) найдем по формуле ([1] 4.23):



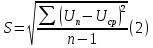
где n – количество измерений.

Найдем сумму квадратов отклонений:



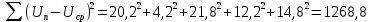
Среднеквадратичное отклонение погрешности результата наблюдений по (2) при n = 5:



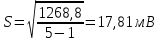
Средняя квадратическая погрешность результата измерения определяется формулой ([1], 4.30):



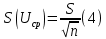
где S −среднеквадратичное отклонение погрешности результата наблюдений (стандартной неопределенности единичного измерения);

n – число измерений.


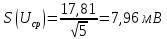
Доверительный интервал ε вычисляется по формуле:



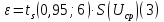
где t_S(P;n) — коэффициент Стьюдента для n измерений при доверительной вероятности Р = 0,9;

Коэффициент Стьюдента для 5 измерений при доверительной вероятности Р = 0,9:

t_S(0,9;5) = 2,015

Границы доверительного интервала погрешности по (3):



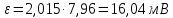
Оставим в погрешности результата 2 значащие цифры.



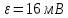
Как видно, систематическая погрешность 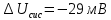по абсолютной величине больше доверительного интервала ε, что доказывает существование систематической погрешности.

Результат измерения в соответствии с правилами представления результата МИ 1317-2004 запишем следующим образом:






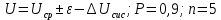
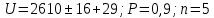
Задача 2. ИЗМЕРЕНИЕ ТОКА И НАПРЯЖЕНИЯ

[1, с. 21-43, 85-110]; [2, с. 30-34, 47-48, 54-109]

Вольтметром постоянного напряжения класса точности 1,5 и электростатическим вольтметром класса точности 4,0 на пределе 250 В измеряют напряжение периодического сигнала, форма которого показана на рис. 2.1. Определите показания приборов, абсолютную и относительную погрешности измерения напряжения этими двумя вольтметрами. Запишите в соответствии с правилами результаты измерений.

---

Т


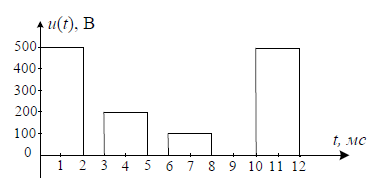
Рис. 2.1 Форма исследуемого напряжения.

Решение:

Запишем аналитическое выражение сигнала в пределах одного периода.



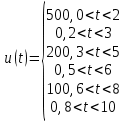
Период сигнала: Т = 10 мс

Вольтметры постоянного напряжения (магнитоэлектрические приборы) измеряют постоянную составляющую или среднее значение сигнала. Определенный интеграл дает площадь, ограниченную графиком исследуемой функции, таким образом, показания шкалы магнитоэлектрического амперметра [1, с. 27, ф.3.1]:



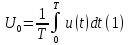
Подставляя аналитическое выражение данного сигнала, получаем:



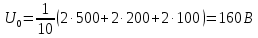
Показание вольтметра постоянного напряжения:

U_пв = U₀ = 160 В

Электростатические вольтметры измеряют действующее значение напряжения, или среднеквадратическое значение [1, с. 27, ф.3.3]:.





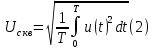
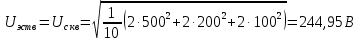
Оценим погрешности.

Относительная погрешность:



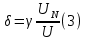
Абсолютная погрешность:



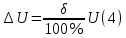
Предел измерения U_N = 250 В

Для вольтметра постоянного напряжения с классом точности γ = 1,5

Относительная погрешность по (3):



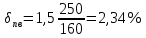
Абсолютная погрешность по (4):



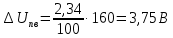
Для вольтметра постоянного напряжения с классом точности γ = 4

Относительная погрешность по (3):



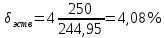
Абсолютная погрешность по (4):



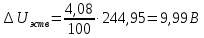
Результат измерения в соответствии с правилами представления результата МИ 1317-2004 запишем следующим образом:
U_пв = (160,0 ± 3,8) B; Р = 0,997, условия измерения нормальные

---

или

U_пв = (160,0 ± 2,3%) B; Р = 0,997, условия измерения нормальные
U_эств = (245 ± 10) B; Р = 0,997, условия измерения нормальные

или

U_эств = (245 ± 4,1%) B; Р = 0,997, условия измерения нормальные
Задача 3. ПРИМЕНЕНИЕ ЭЛЕКТРОННО-ЛУЧЕВОГО ОСЦИЛЛОГРАФА

[1, с. 166-192, 203-205]; [2, с. 171-204]

На экране осциллографа появилось изображение в виде окружности. Постройте для этого случая в одном и том же масштабе времени сигналы, поданные на вертикально и горизонтально отклоняющие пластины электронно-лучевой трубки осциллографа

Решение:

Изображение в виде окружности на экране осциллографа представляет собой фигуру Лиссажу — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Для того, чтобы на экране образовалась окружность необходимо выполнение условия между частотами сигнала и развертки:

u_c = u_y∙sin(ωt); u_p = u_x∙sin(ωt + π/2)

u_y = u_x

Образование изображения на экране ЭЛТ при воздействии двух напряжений — развертки (u_p = u_x) и сигнала (u_c = u_y) — соответственно на пластинах X и Y показано на рис. 3.2. Период, развертки условно разбит на пять равных интервалов с грани­цами, отмеченными на рис. 3 через t₀, t₁....t₅,. В момент t₀ u_y = 0, а u_x имеет положительное максимальное значение, и световое пятно находится в точке 1. В момент t₂ напряжение сигнала также имеет положительное максимальное значение, а u_y = U_max и пятно находится в точке 2. Аналогичным путем можно найти положе­ние точек 2, 3, ... 8, на экране ЭЛТ.

В последующие циклы развертки образование осциллограммы будет происходить так же, причем все ее точки совпадут с аналогичными точками осциллограммы, изо­браженной на рис. 3.2. Таким образом, наблюдатель видит изображение, образован­ное наложением на одни и те же места экрана целой серии осциллограмм. Число таких первичных изображений, зафиксированных в зрительном образе, зависит от периода развертки, длительности послесвечения люминофора и зрительной памяти человека.


2. Область сигнала на входе Y

осциллографа

1. Область экрана осциллографа

---

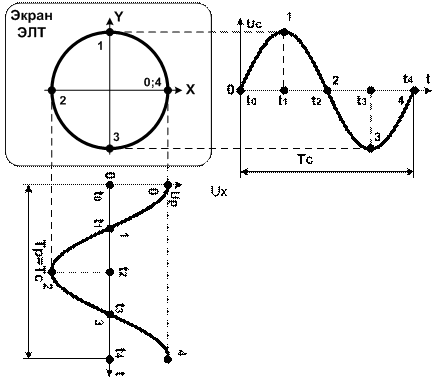
4. Формируемое изображение

3. Область сигнала на входе Х

осциллографа


Задача 4. ЦИФРОВЫЕ ИЗМЕРЕНИЯ ЧАСТОТЫ И ИНТЕРВАЛОВ ВРЕМЕНИ

[1, с. 213-221]; [2, с. 252-255, 273-276]

Постройте график зависимости суммарной относительной погрешности электронно-счетного (цифрового) частотомера в режиме измерения частоты от частоты измеряемого сигнала в диапазоне 10 Гц − 10 МГц. Воспроизведите соответствующую формулу и назовите составляющие суммарной погрешности. Значение относительной погрешности опорного кварцевого генератора частотомера примите равным ± 5·10^-7. Время измерения (время счета) примите равным t₀ = 10 с. При построении используйте логарифмический масштаб по осям координат. Оцените абсолютную погрешность измерения частоты сигнала 543210,9878 кГц при указанном времени счета. Запишите результат измерения с указанием всех значащих цифр, которые будут отображены на отсчетном устройстве частотомера.

Решение:

Результирующая (суммарная) предельная относительная погрешность измерения частоты 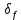определяется двумя составляющими [2, форм. 5.5].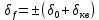



где 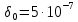 предельная погрешность опорного генератора;

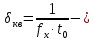предельная погрешность квантования (дискретности);

f_x - частота измеряемого сигнала, Гц.

t₀ – время счета, c.





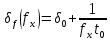
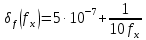
Построим график, задаваясь частотой измеряемого сигнала в диапазоне 10 Гц − 10 МГц. Результаты расчёта сведём в Таблицу №1:













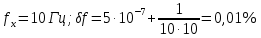
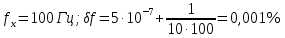
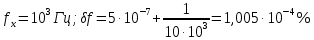
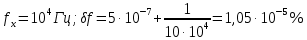
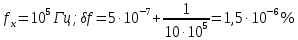
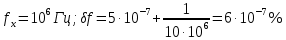
Таблица №1

fх , Гц	10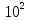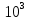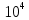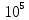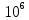
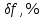	0,01	0,001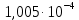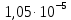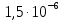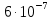

---

Смотрите также файлы

• Содерж.docx

• Фамилия Имя Класс Химия, 9 класс. Вариант хи4602.docx

• Практическая работа 1. Арм менеджера.docx

• Перспективы возделывания калины в почвенноклиматических условиях Республики Беларусь.docx

• Контрольная работа состоит из двух частей теоретическая и практическая. Для выполнения теоретической части контрольной работы необходимо выбрать 1 тему и раскрыть ее на 35 страниц из предложенного списка по последней цифре зачетной книжки.docx