Частное профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ»

Практическое задание

по	Статистика

дисциплине

Выполнил(а) студент(ка)	Морозов Сергей Александрович
			фамилия имя отчество
Идентификационный номер:		2109-0710-2100796

Пермь 2022г.Задача №1Имеются следующие данные за год по заводам одной промышленной компании:

Завод	Среднее число рабочих, чел.	Основные фонды, млн руб.	Продукция, млн руб.	Завод	Среднее число рабочих, чел.	Основные фонды, млн руб.	Продукция, млн руб.
1	700	250	300	9	1 400	1 000	1 600
2	800	300	360	10	1 490	1 250	1 800
3	750	280	320	11	1 600	1 600	2 250
4	900	400	600	12	1 550	1 500	2 100
5	980	500	800	13	1 800	1 900	2 700
6	1 200	750	1 250	14	1 700	1 750	2 500
7	1 100	700	1 000	15	1 900	2 100	3 000
8	1 300	900	1 500

---

На основании приведенных данных составьте групповую таблицу зависимости выработки на одного рабочего от величины заводов по числу рабочих. Число групп – три.РЕШЕНИЕ:Выработку на одного рабочего определим путем деления общего объема продукции на число рабочих.

Завод	Основные фонды, млн. руб.	Выработка на одного рабочего, тыс. руб.
1	250	428,6
2	300	450
3	280	426,7
4	400	666,7
5	500	816,3
6	750	1041,7
7	700	909,1
8	900	1153,8
9	1000	1142,9
10	1250	1208,1
11	1600	1406,3
12	1500	1354,8
13	1900	1500
14	1750	1470,6
15	2100	1578,9

Величина интервала Получаем следующие группы:1-я 250-866,7 2-я 866,7-1483,4 3-я 1483,4-2100,1Для формирования аналитической группировки строим вспомогательную таблицу:

№ группы	Интервал	№ завода	Основные фонды, млн. руб	Выработка на одного рабочего, тыс. руб.
1	250-866,7	1	250	428,6
		2	300	450
		3	280	426,7
		4	400	666,7
		5	500	816,3
		6	750	1041,7
		7	700	909,1
	Итого группы	7	3180	4739,1
2	866,7-1483,4	8	900	1153,8
		9	1000	1142,9
		10	1250	1208,1
	Итого группы	3	3150	3504,8
3	1483,4-2100,1	11	1600	1406,3
		12	1500	1354,8
		13	1900	1500
		14	1750	1470,6
		15	2100	1578,9
	Итого группы	5	8850	7311

---

На основании разработочной таблицы формируем аналитическую группировку:

№ группы	Интервал	Число заводов	Основные фонды, млн. руб.			Выработка на одного рабочего, тыс. руб.
			Всего	На 1 з-д	Всего		На 1 з-д
1	250-866,7	7	3180	454,29	4739,1		677,01
2	866,7-1483,4	3	3150	1050	3504,8		1168,27
3	1483,4-2100,1	5	8850	1770	7311		1462,2
	Итого	15	15180	1012	15554,9		1036,99

На основании аналитической группировки необходимо сделать вывод о прямой связи между переменными, т. к. они одновременно в среднем растут. Задача №2Выпуск продукции на заводе в 2020 г. составил 160 млн руб. По плану на 2021 г. предусматривалось выпустить продукции на 168 млн руб., фактически же выпуск составил 171,36 млн руб. Вычислите относительные величины планового задания и выполнения плана.РЕШЕНИЕ:Относительный показатель планового заданияПлан составил 105%, т. е. предусматривается увеличить показатели выпуска продукции на 5%.Относительный показатель выполнения плана:

---

План выполнен на 102%, т. е. перевыполнен на 2%.Задача №3На основании данных, представленных в таблице, определите установленную среднюю продолжительность трудового дня производственного рабочего по заводу в целом:

Показатель	1 цех	2 цех	3 цех	4 цех
Количество смен	3	3	2	1
Число рабочих в смену	600	800	400	200
Продолжительность смены	8	8	8	6

РЕШЕНИЕ:Задача №4Имеются следующие данные о распределении рабочих цеха по размеру месячной заработной платы:

Размер зарплаты, тыс. руб.	до 5,0	5,0-7,5	7,5-10,0	10,0-12,5	свыше 12,5
Число рабочих, чел.	15	15	25	65	30

Определите среднюю месячную зарплату рабочих цеха, моду и медиану, среднеквадратическое отклонение и коэффициент вариации.РЕШЕНИЕ:Таблица 1. Расчет вспомогательных значений для определения показателей ряда распределения

№	Размер зарплаты,  тыс. руб.	Середина интервала, Xi	Число рабочих, чел., fi			Кумулята, S
1	до 5,0	3,75	15	56,25	601,0335	15
2	5,0-7,5	6,25	15	93,75	220,0335	30
3	7,5-10,0	8,75	25	218,75	44,2225	55
4	10,0-12,5	11,25	65	731,25	88,9785	120
5	свыше 12,5	13,75	30	412,5	404,067	150
	Итого		150	1512,5	1358,335

---

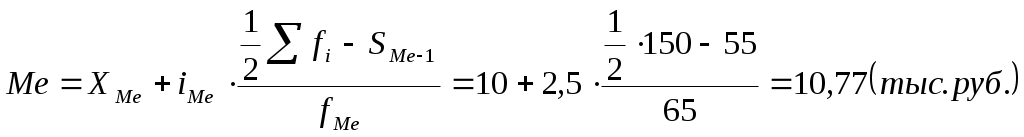
Средняя месячная зарплата рабочих цеха:Мода:Большинство рабочих имеют среднюю заработную плату 11,33 тыс. рублей.Медиана:Половина рабочих имеют среднюю заработную плату менее 10,77 тыс. рублей, другая половина – более 10,77 тыс. рублей.Дисперсия:Среднее квадратическое отклонение:Коэффициент вариации:, следовательно, совокупность считается однородной.Задача №5Объем продукции на промышленном предприятии повысился в 2016 году по сравнению с 2011 годом на 100 млн рублей в сопоставимых ценах, или на 25 %. В 2021 году объем продукции увеличился по сравнению с 2016 годом на 20 %.Определите:

1. 
   объем выпуска продукции предприятия в 2011, 2016, 2021 годах;
   
2. 
   среднегодовые темпы прироста выпуска продукции за:  а) 2011-2021 гг.; б) 2016-2021 гг.; в) 2011-2016гг.;
   

 РЕШЕНИЕ:Объёмы продукции обозначим: А-2011, В-2016, С-2021Значит B(2016)=1.25*A, C(2021)=1.2*BЗная что, 0.25*A=100 (млн руб.), получаем:A(2011)=100/0.25= 400 (млн.руб.)B(2013)=1.25*400= 500 (млн руб.)C(2018)=500*1.2= 600 (млн руб.)Темпы прироста:A) 2011-2021 гг.; Б) 2016-2021 гг.;     В) 2011-2016г. A) 0,25/5=0,05 или 5%Б) 0,2/2=0,04 или 4%В) (600-400)/400/10 = 200/400/10 = 0,5 / 10 = 0,05 или 5%Задача №6

---

Смотрите также файлы

• Курсовая работа по дисциплине Теория электрической связи (наименование учебной дисциплины согласно учебному плану).docx

• Наша партия Мудрости Совета против этого. Мы говорим нет этому хаосу!.docx

• Лабораторная работа по дисциплине правоведение Группа 22П176в Студент.docx

• Бизнес Идея Кальянный магазин Морозов Сергей Александрович.pptx

• Приложение 4 Педагогическая копилка фикультминуток разного видадля уроков в начальной школе.docx