Файл: Тест по статистике.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 74

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



Тест по статистике

  1. Что понимается под вероятностью события А в случае, когда результаты опыта образуют полную группу равновозможных и несовместных элементарных исходов ?
Ответ : 1. Сумма числа всех элементарных исходов благоприятных для события А .2. Отношение числа всех элементарных исходов благоприятных для события А к общему числу всех элементарных исходов.3. Отношение общего числу всех элементарных исходов к числу всех элементарных исходов благоприятных для события А.

  1. Набирая номер телефона, абонент забыл одну цифру и набрал её наудачу. Найти вероятность того, что набрана нужная цифра.
Ответ : 1. 1/10.2. 1/7 .3. 7/10.

  1. Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4.
Ответ : 1. 1/36.2. 3/36 .3. 4/36 .

  1. Как связаны между собой число сочетаний из n по m –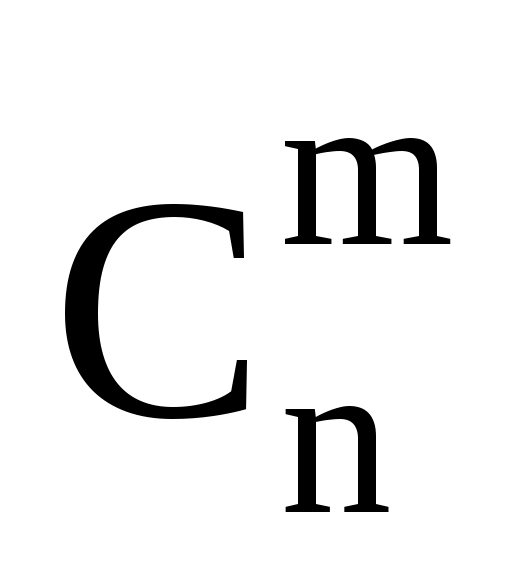 и число перестановок из n по m – ?
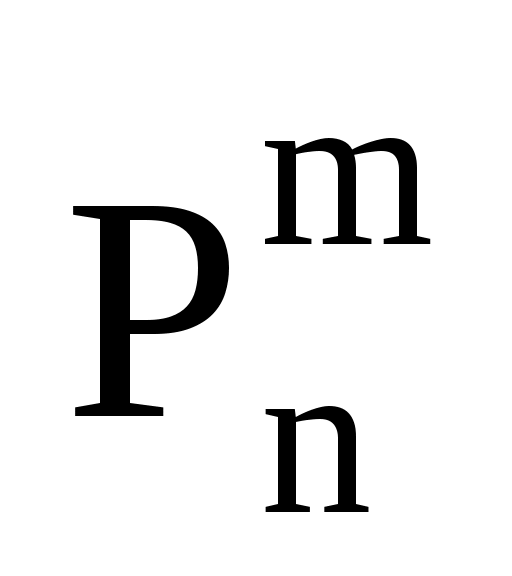Ответ : 1. = m! .2. = m!.3. = m!.

  1. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартных.
Ответ : 1. 4/6 .2. (·)/ .3. (+) /

.


  1. В каком случае вероятность суммы двух событий равна сумме вероятностей этих событий, т.е. P(A + B) = P(A) + P(B) .
Ответ : 1. Если в результате опыта эти события не могут наступить одновременно.

  1. Если событие А наступает только при условии наступления события В.

  2. Если событие В наступает только при условии наступления события А

  1. Стрелок стреляет по мишени, разделённой на 3 области. Вероятность попадания в первую область равна 0,45 , а во вторую 0,35. Найти вероятность того, что стрелок при одном выстреле попадёт либо в первую, либо во вторую область.
Ответ : 1. 1.2. 0,2 .

  1. 0,8 .

  1. Чему равна вероятность события В при условии, что произошло событие А, т.е. РА(В) ?
Ответ : 1. Р(АВ).

  1. Р(АВ)/Р(А).

  2. Р(АВ)/Р(В)

  1. Используя правило умножения вероятностей найти вероятность того, что, извлекая наугад из коробки с 5-ю белыми и 4-мя чёрными шарами последовательно два шара (без возврата), в первый раз извлекается белый шар, а во второй раз чёрный шар.
Ответ : 1. 5/9 · 4/8 .2. 5/9 · 4/9 .

  1. 2/9 .

  1. Если событие F может наступить только при условии наступления одного из событий А1, А2, . . . , Аn , образующих полную группу, то как по формуле полной вероятности найти вероятность события F ?
Ответ : 1. P(F) = P(А1) · P(А2) · . . . · P(Аn) . 2. P(F) = P(А1) + P(А2) +  . . . + P(Аn).3. P(F) = P(А1) + P(А2) + . . . + P(Аn) .

  1. В каком случае вероятность вытащить на экзамене «хороший» билет для студента выше: когда он берёт наудачу билет первым или вторым ? Можно считать, что студент подготовил только 10 билетов из 20.
Ответ : 1. Вероятность выше, когда студент берёт билет первым.2. Вероятность выше, когда студент берёт билет вторым.

  1. Вероятности в обоих случаях совпадают.

  1. Если событие F может наступить только при условии наступления одного из событий А1, А2, . . . , Аn , образующих полную группу, то как по формуле Байеса найти условную вероятность ?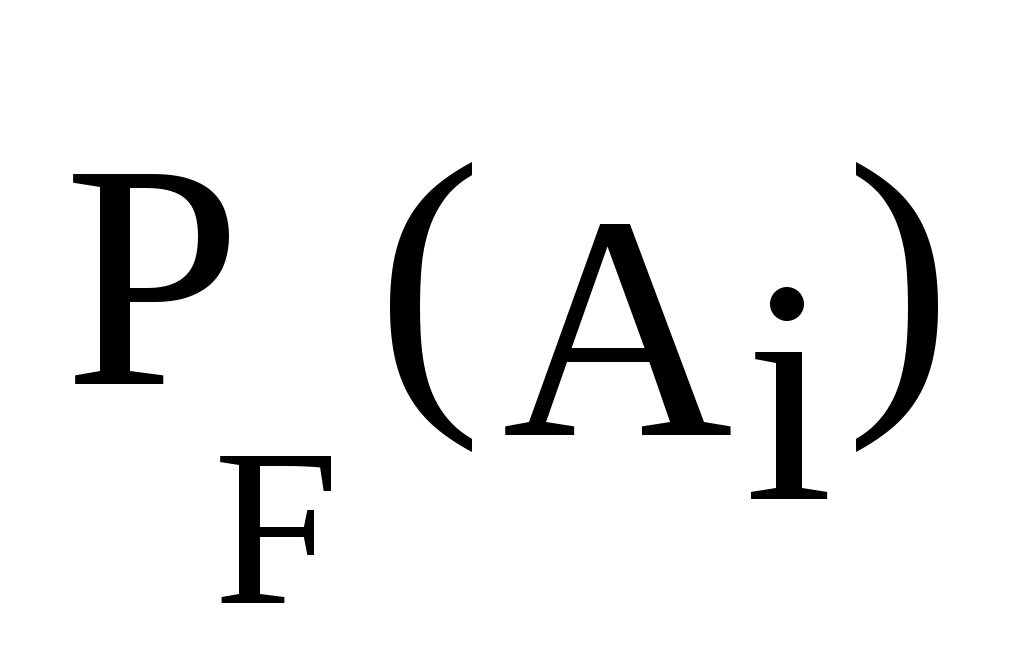
Ответ : 1. = P(А1) · P(А2) · . . . · P(Аn) .2. = ( P(А1) · P(А2) · . . . · P(Аn) ) / P(F) .3. = ( P(Аi) ) / P(F) .

  1. Если вероятность наступления события А в каждом испытании постоянна и равна р, то чему равна вероятность Рn(k) – наступления события А ровно k раз в n независимых испытаниях ?
Ответ : 1. pk .2. pk(1-p)n-k.3. pn-k (1-p)k .

  1. Вероятность для каждого из 10 банков разориться в течении года равна 0,1 . Найти вероятность того, что за год разорятся точно 3 из этих 10 банков.
Ответ : 1. (0,1)3 (0,9)7 .2. (0,1)3 .3. (0,1)3 (0,9)7 .

  1. Используя таблицу значений функции Пуассона, найти вероятность того, что из 10 000 упаковок товара ровно 10 упаковок составлены с нарушением стандарта ( Р10000(10) ), если вероятность нарушения стандарта для одной упаковки равна 0,001 .
Ответ : 1. Р10000(10) ≈ 0,125 .2. Р10000(10) ≈ 0,213 .3. Р10000(10) ≈ 0,012 .

  1. Пусть закон распределения дискретной случайной величины Х задаётся таблицей :

xi
1
3
4
6
9
10

pi
0,1
0,1
0,2
0,3
0,1
0,2

. Определить из какого интервала (1;5) или (5;8) случайная величина Х примет значение с большей вероятностью ?

Ответ : 1. Р(1 P(5
2. Р(1


  1. Р(1




  1. Как определяется функция распределения случайной величины Х – F(х) ?

Ответ : 1. F(х) = P(0

  1. F(х) = P(X

  2. F(х) = P(X>x).

  1. Пусть функция распределения случайной величины Х имеет вид: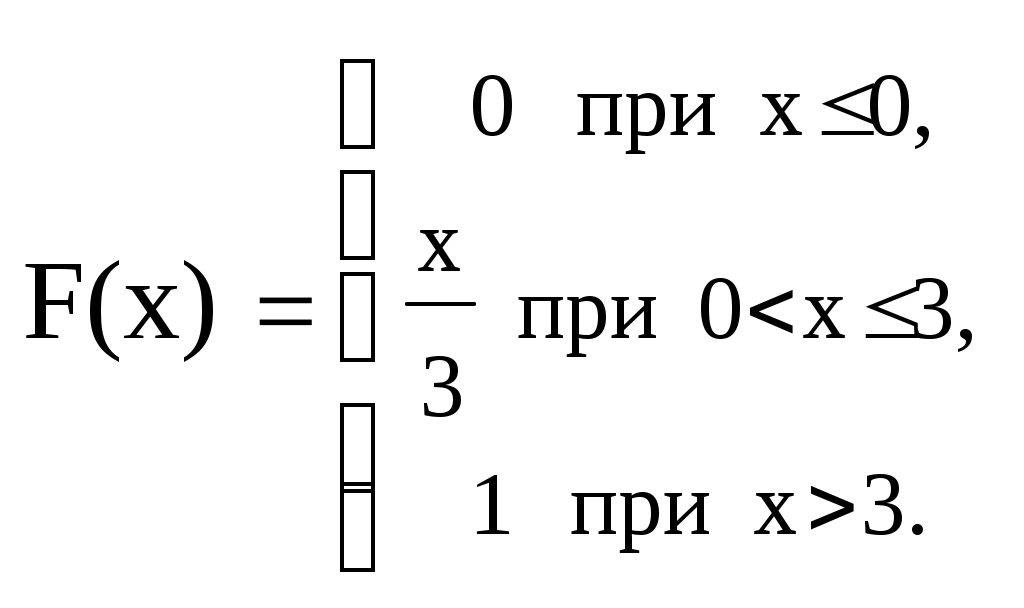 . Найти вероятность того, что случайная величина Х примет значение из интервала [1;4).

Ответ : 1. Р(1≤X<4) = F(1) = 1/3.

2. Р(1≤X<4) = F(4) – F(1) = 2/3 .

3. Р(1≤X<4) = 4/3 – 1/3 = 1.

  1. Какая из числовых характеристик дискретной случайной величины характеризует среднее значение этой величины ?

Ответ : 1. Дисперсия.

2. Математическое ожидание.

3. Среднее квадратическое отклонение.


  1. Найти математическое ожидание числа лотерейных билетов, на которые выпадает выигрыш, если приобретено 20 билетов, причём вероятность выигрыша по одному билету равна 0,4.

Ответ : 1. Математическое ожидание равно 20/2 = 10 билетам.

2. Математическое ожидание равно 20/4 = 5 билетам .

3. Математическое ожидание равно 20·0,4 = 8 билетам.

  1. Найти математическое ожидание суммы числа очков, которые могут выпадать при бросании двух игральных костей, если математическое ожидание числа очков, которое может выпадать на первой кости (на второй кости) равно 7/2.

Ответ : 1. Математическое ожидание равно 7/2 + 7/2 = 7 .

2. Математическое ожидание равно 7/2.

3. Математическое ожидание равно 7/2 · 7/2 = 49/4.



  1. Чему равна вероятность того, что непрерывная случайная величина Х примет одно определённое значение хо, т.е. найти Р(Х = хо) .

Ответ : 1. Р(Х = хо) = 0.

2. Р(Х = хо) = 1 .

3. Р(Х = хо) – зависит от числового значения хо .


  1. Как связаны функция распределения F(х) и плотность вероятности φ(х) непрерывной случайной величины Х ?

Ответ : 1. F(x) = φ'(x) .

2. φ(x) = F' (x) .

3. φ(х) = .

  1. Дана плотность вероятности случайной величины Х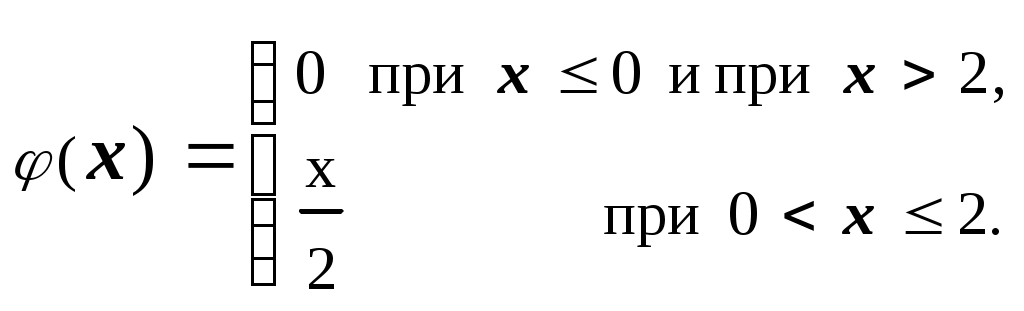 . Найти вероятность того, что случайная величина Х примет значение из интервала [1; 2], т.е. Р(1≤X≤2) .

Ответ : 1. Р(1≤X≤2) = .

2. Р(1≤X≤2) = φ(2) – φ(1) = 1/2 .

3. Р(1≤X≤2) = φ(2) = 1.

  1. Текущая цена акций может быть смоделирована с помощью нормального закона распределения с математическим ожиданием а = 10 ден.ед. и средним квадратическим отклонением σ = 0,1 ден.ед. . Найти вероятность того, что цена акций меньше 10,1 ден.ед. , т.е. Р(X.<10 ,1).

Ответ : 1. Р(X<10 ,1) = Ф( (10,1– 0,1) /0,1 ) ≈ 1,7 , где Ф(х) – функция Лапласа.

2. Р(X<10 ,1) = 0,5 + 0,5Ф( (10,1– 10) /0,1 ) ≈ 0,8 , где Ф(х) – функция Лапласа.

3. Р(X<10 ,1) ≈ 0,5.

  1. Коробки конфет упаковываются автоматически и, следовательно, можно считать, что их масса Х имеет нормальный закон распределения. Известно, что средняя масса коробки равна 250г, а среднее квадратическое отклонение 5г . Определить границы, в которых с вероятностью близкой к 1 будет колебаться масса упакованной коробки Х .

Ответ : 1. 235г ≤ Х ≤ 265г .

2. 245г≤ Х ≤ 255г .

3. 250г ≤ Х ≤ 255г .

  1. Случайная величина Х имеет нормальный закон распределения с математическим ожиданием а = 25 и средним квадратическим отклонением σ = 2 . Найти вероятность попадания Х в интервал [22; 28] , т.е. Р(22≤X≤28) .

Ответ : 1. Р(22≤X≤28) = Ф(3/2) ≈ 0,866 , где Ф(х) – функция Лапласа.

2. Р(22≤X≤28) = Ф(28/25) ≈ 0,737 , где Ф(х) – функция Лапласа.

3. Р(22≤X≤28) ≈ 0,999.

  1. Если случайная величина Х равна сумме 1000 независимых случайных величин: Х1, Х2, … , Х1000 , имеющих один и тот же закон распределения, одинаковые математические ожидания и одинаковые дисперсии, то какой вывод можно сделать о характере распределения случайной величины Х

Ответ : 1. М(Х) = М(Хi) , где i = 1, 2, … , 1000.

2. D(Х) = D(Хi) , где i = 1, 2, … , 1000.

3. Закон распределения случайной величины Х близок к нормальному.

  1. Если для случайной величины Х имеется полигон частот, построенный по некоторой выборочной совокупности случайной величины Х, то можно ли по этому полигону частот найти значения выборочной средней и выборочной дисперсии случайной величины Х ?

Ответ : 1. Нет, нельзя.

2. Да, можно.

3. Можно только в том случае, если известен объём всей генеральной совокупности.

  1. В каком случае статистическая оценка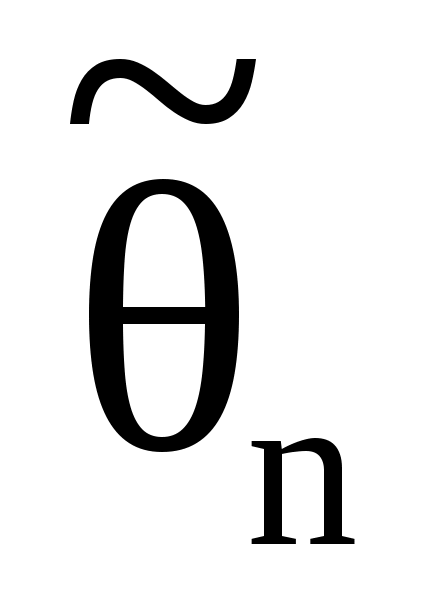 параметра распределения 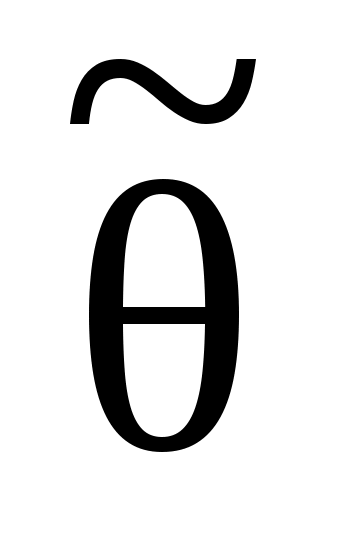называется несмещённой ?

Ответ : 1. Если математическое ожидание равно 0, т.е. М( ) = 0 .

2. Если математическое ожидание равно 1, т.е. М( ) = 1.

3. Если математическое ожидание равно , т.е. М( ) = .



  1. В каком случае статистическая оценка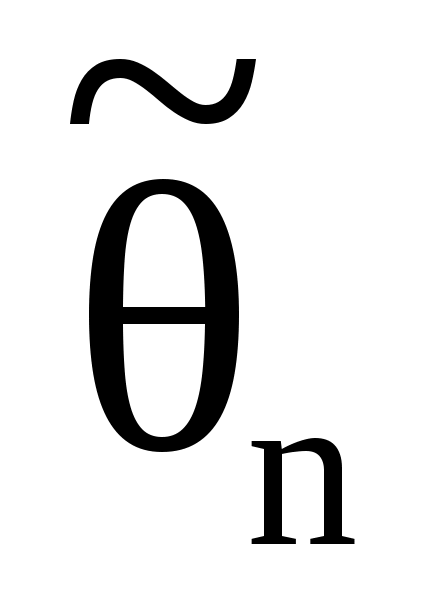 параметра распределения 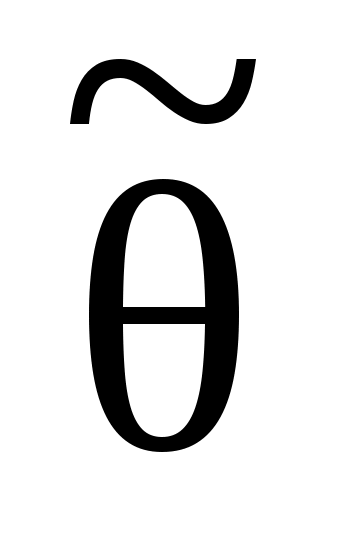называется состоятельной ?

Ответ : 1. Если дисперсия стремится к 0, т.е. 0 при .

2. Если дисперсия равно 1, т.е. D( ) = 1.

3. Если математическое ожидание равно 0, т.е. М( ) = 0 .


  1. Является ли выборочная средняя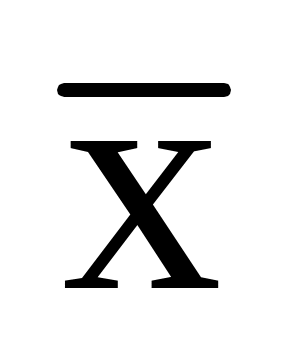 несмещённой и состоятельной оценкой для генеральной средней ?

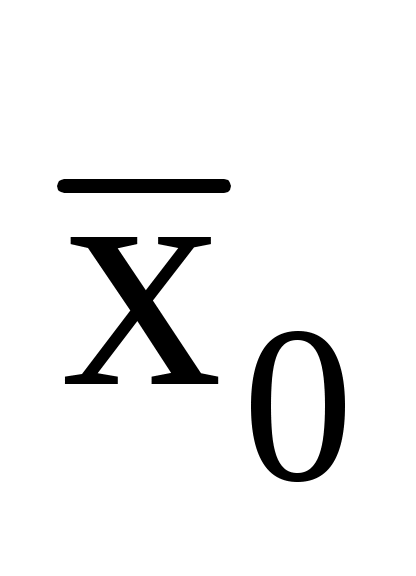Ответ : 1. Да, - несмещённая и состоятельная оценка для

2. Нет, - смещённая и состоятельная оценка для .

3. Нет, - смещённая и несостоятельная оценка для .



  1. Является ли выборочная дисперсия s2 несмещённой и состоятельной оценкой для генеральной дисперсии σ2 ?

Ответ : 1. Да, s2 - несмещённая и состоятельная оценка для σ2 .

2. Нет, s2 - смещённая и состоятельная оценка для σ2.

3. Нет, s2 - смещённая и несостоятельная оценка для σ2 .


  1. При обследовании производительности труда рабочих одного цеха в отчётном году была произведена случайная выборка. Известно, что средняя производительность рабочих по выборке равна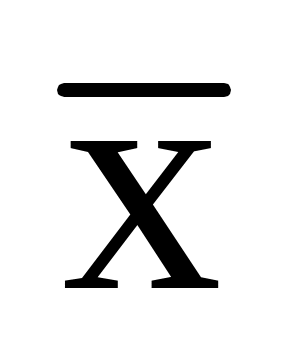 = 110%, а средняя квадратичная ошибка выборки для средней равна 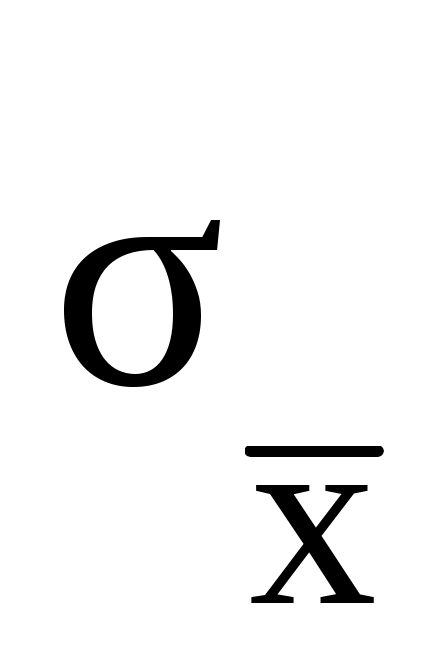= 0,8%. Найти вероятность того, что средняя производительность рабочих цеха ( 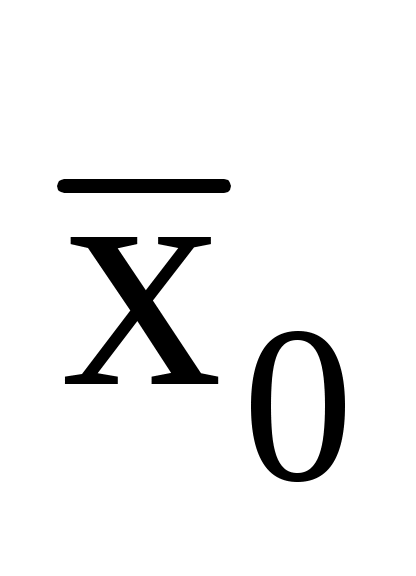) отличается по модулю от средней производительности по выборке ( 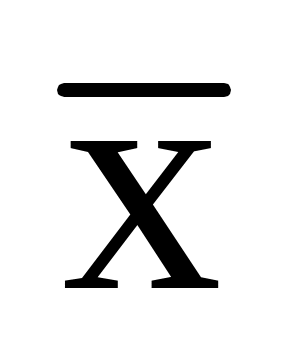) не более чем на 1%, т.е. Р( | 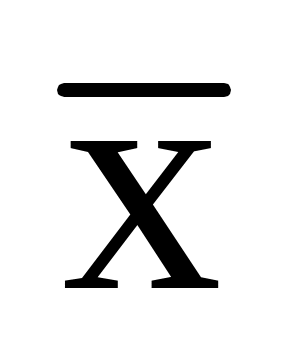– 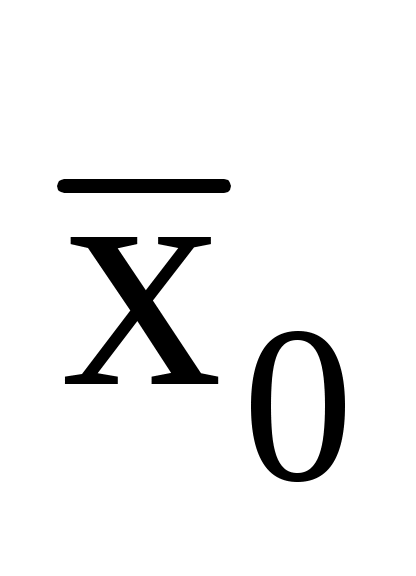| ≤ 1%).

Ответ : 1. Р( | – | ≤ 1%) = Ф(1) ≈ 0,68 , где Ф(х) – функция Лапласа.

2. Р( | – | ≤ 1%) = Ф(1/0,8) ≈ 0,79 , где Ф(х) – функция Лапласа.

3. Р( | – | ≤ 1%) = Ф(0,8) ≈ 0,58, где Ф(х) – функция Лапласа.


  1. Из большой партии деталей для проверки произведена случайная выборка. Доля нестандартных деталей в выборке равна w = 0,8 , а средняя квадратичная ошибка выборки для доли равна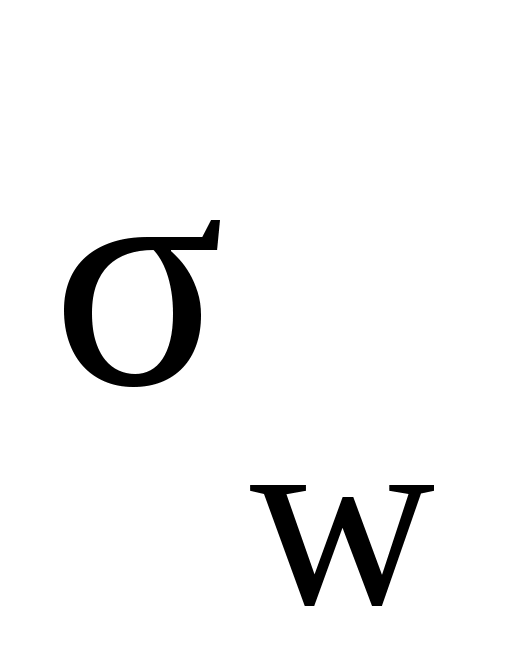 = 0,02. Найти вероятность того, что доля нестандартных деталей во все партии (р) отличается по модулю от доли нестандартных деталей в выборке (w) не более чем на 0,03, т.е. Р( | р – w | ≤ 0,03 ) .

Ответ : 1. Р( | р – w | ≤ 0,03 ) = Ф(0,8) ≈ 0,79 , где Ф(х) – функция Лапласа.

2. Р( | р – w | ≤ 0,03 ) = Ф(0,02/0,03) ≈ 0,50 , где Ф(х) – функция Лапласа.

3. Р( | р – w | ≤ 0,03 ) = Ф(0,03/0,02) ≈ 0,87 , где Ф(х) – функция Лапласа.

  1. Известно, что средние размеры детали, найденные по случайной выборке равны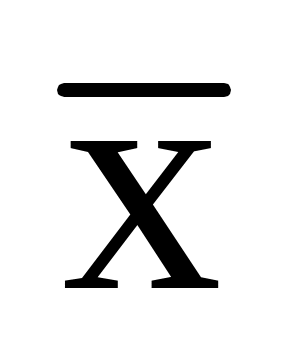 = 30, а средняя квадратичная ошибка выборки для средней равна 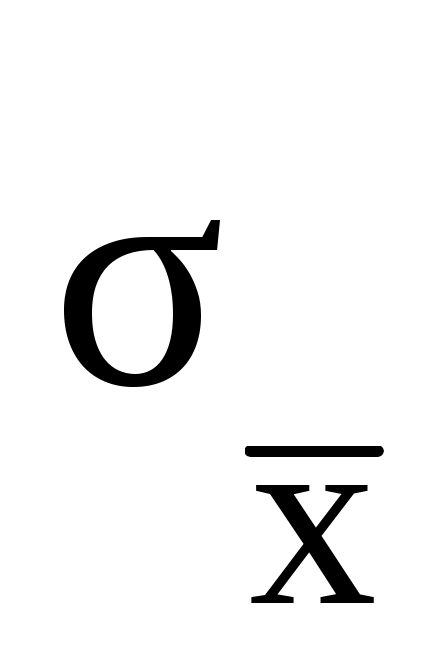= 0,6 . Найти с надёжностью 0,99 (γ = 0,99) ошибку репрезентативности для выборочной средней 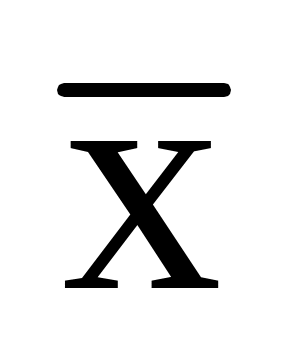, т.е. найти Δ , где | 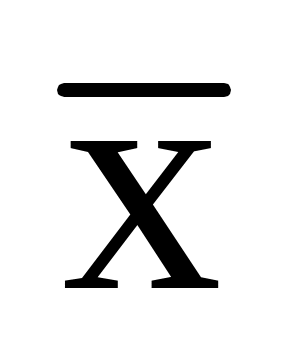– 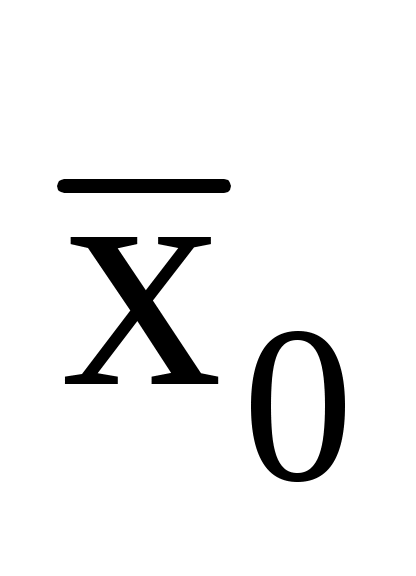| ≤ Δ , 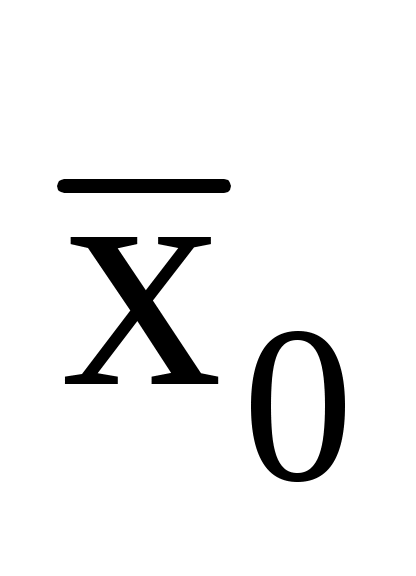- средние размеры детали во всей партии.

Ответ : 1. Δ = Ф-1 (0,99)·0,6 ≈ 1,5 , где Ф-1(х) – функция обратная к функции Лапласа.

2. Δ = Ф (0,99)·0,6 ≈ 0,4 , где Ф(х) – функция Лапласа.

3. Δ ≈ 0,6.

  1. Найти границы (доверительный интервал: [w – Δ ; w + Δ] ), в которых заключена доля вкладчиков банка, имеющих вклад более 10 000 руб., если доля таких вкладчиков в случайной выборке равна w = 70%, при этом ошибка выборочной доли (ошибка репрезентативности) равна Δ = 10%.

Ответ : 1. [60% ; 70%] .

2. [60% ; 80%] .

3. [70% ; 80%] .

  1. Как изменится ошибка репрезентативности Δ для выборочной доли, если сохраняя все параметры выборки увеличить надёжность (доверительную вероятность γ) этой ошибки ?

Ответ : 1. Ошибка репрезентативности Δ увеличится.

2. Ошибка репрезентативности Δ уменьшится.

3. Ошибка репрезентативности Δ не изменится.

  1. Можно ли «сжать» доверительный интервал для генеральной средней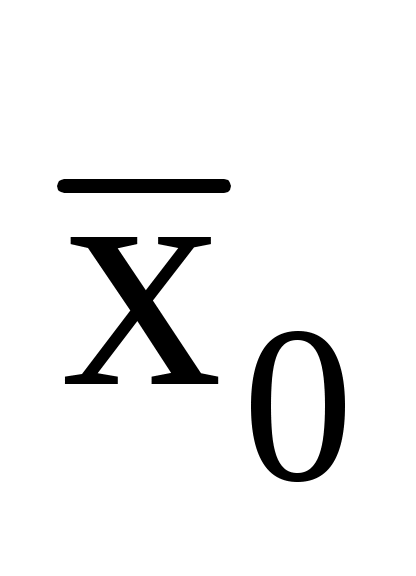 : [ 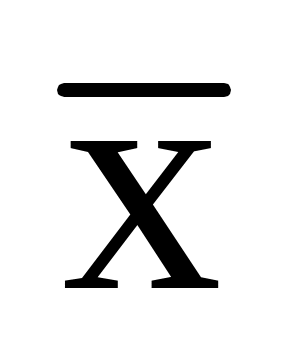– Δ ; 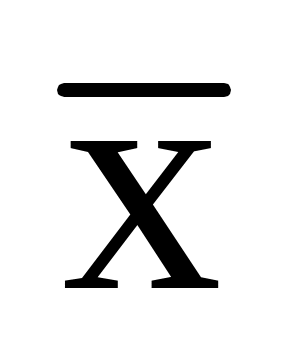+ Δ], не меняя параметров выборки ?

Ответ : 1. Нет нельзя.

2. Можно, если увеличить доверительную вероятность γ .

3. Можно, если уменьшить доверительную вероятность γ.


  1. Известно, что доверительный интервал (найденный по случайной выборке) для доли нестандартных деталей во всей партии деталей (р) имеет вид: [0,02 ; 0,04], а доля нестандартных деталей в выборке равна w = 0,03. Найти ошибку репрезентативности для доли нестандартных деталей в выборке, т.е. такое минимальное Δ,что | w – р | ≤ Δ.

Ответ : 1. Δ = 0,02 .

2. Δ = 0,01 .

3. Δ = 0,005 .

  1. В чём состоит ошибка первого рода при проверке статистической гипотезы ?

Ответ : 1. Принять гипотезу, когда она неверна.

2. Отвергнуть гипотезу, когда она верна.

3. Отвергнуть как саму гипотезу, так и её отрицание.


  1. В чём состоит ошибка второго рода при проверке статистической гипотезы ?

Ответ : 1. Принять гипотезу, когда она неверна.

2. Отвергнуть гипотезу, когда она верна.

3. Принять как саму гипотезу, так и её отрицание.


  1. Что называется уровнем значимости критерия при проверке статистической гипотезы ?

Ответ : 1. Вероятность допустить ошибку 2-го рода.

2. Вероятность не допустить ошибку 1-го рода.

3. Вероятность допустить ошибку 1-го рода.


  1. Что называется мощностью критерия при проверке статистической гипотезы ?

Ответ : 1. Вероятность отвергнуть гипотезу, когда она неверна.

2. Вероятность допустить ошибку 2-го рода.

3. 1 – α , где α – значение уровнем значимости критерия.



  1. Выработка
    94-104
    104-114
    114-124
    124-134
    134-144

    Количество

    рабочих
    6
    20
    45
    24
    5
    На уровне значимости критерия  = 0,05 проверить с помощью критерия Пирсона гипотезу о нормальном распределении случайной величины Х – выработки рабочих одного цеха, если известны распределение 100 рабочих цеха по выработке: и наблюдаемое значение статистики2=1,45.


Ответ : 1. Гипотезу следует отвергнуть.

2. Гипотезу следует принять.

3. Критерий Пирсона не позволяет дать ответ на поставленный вопрос.


  1. Пусть с помощью критерия Пирсона проверяется гипотеза о нормальном распределении. Из статистических данных известно, что значение наблюдаемой статистики равно 2 = 3,64 , а число степеней свободы равно k = 3. По таблице найти наибольшее значение уровня значимости критерия , при котором гипотеза будет принята.

Ответ : 1.  = 0,30 .

2.  = 0,01 .

3.  = 0,90 .

  1. Известно, что выборочный коэффициент корреляции между величиной производственных фондов Х и выработкой продукции Y равен r(X,Y) = 0,93. Описать характер связи между случайными величинами X и Y.

Ответ : 1. Связь между X и Y близка к линейной: y = kx + b , где k<0 .

2. Между X и Y линейная связь отсутствует.

3. Связь между X и Y близка к линейной: y = kx + b , где k>0.


  1. Владельцу акций предприятия Y стало известно, что акции предприятия Х скоро упадут в цене. Произведя финансовый и статистический анализ, удалось установить, что коэффициент корреляции между стоимостью акций этих предприятий отрицательный и равен (–0,93) . В сложившейся ситуации какие действия с акциями предприятия Y следует предпринять их владельцу ?

Ответ : 1. Следует срочно продавать все акции предприятия Y .

2. Следует повременить с продажей акций предприятия Y, ожидая роста их стоимости.

3. Продать ровно половину акций предприятия Y.

  1. Если уравнение линейной регрессии, связывающее цены на нефть – Х с индексом нефтяных компаний – Y имеет вид: y = 10x + 3800, то чему приблизительно равен индекс нефтяных компаний при цене нефти в 20 ден.ед. ?

Ответ : 1. Индекс нефтяных компаний равен 4200.

2. Индекс нефтяных компаний равен 4000.

3. Индекс нефтяных компаний равен 3600.

  1. Если коэффициент корреляции между случайными величинами Х и Y близок к нулю, т.е. r(X,Y) ≈ 0, то какой вывод можно сделать о характере связи между случайными величинами Х и Y ?

Ответ : 1. Между случайными величинами X и Y отсутствует линейная связь .

2. Между случайными величинами X и Y имеется линейная связь.

3. Между случайными величинами X и Y нет никакой статистической зависимости. 0>10>10>10>10>

Смотрите также файлы