Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная/очно-заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Моделирование экономических процессов
Группа 20Э211
Студент
Улинич Н.К


МОСКВА 2023
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
№1. Составить план производства продукции, обеспечив максимум прибыли, учитывая ограничения, заданные в таблице 1.

Таблица 1. Линейная оптимизация

	Расход сырья (доли)				Прибыль от реализации единицы продукции, руб.
	Сырье 1	Сырье 2	Сырье 3	Сырье 4
Продукт 1	0,2	0,3	0,1	0,4		120
Продукт 2	0,4	0,1	0,3	0,2		150
Продукт 3	0,6	0,1	0,1	0,2		110
Наличие сырья на складе, кг	850	640	730	1000

Решение:

Подготовим исходные данные для решения задачи в MS Excel:

---

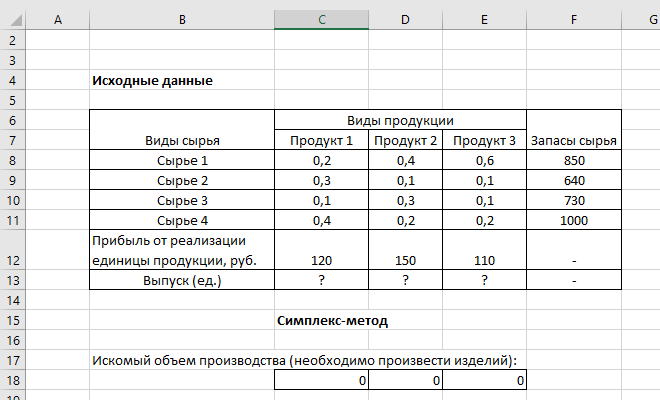Далее составим целевую функцию (максимум прибыли):


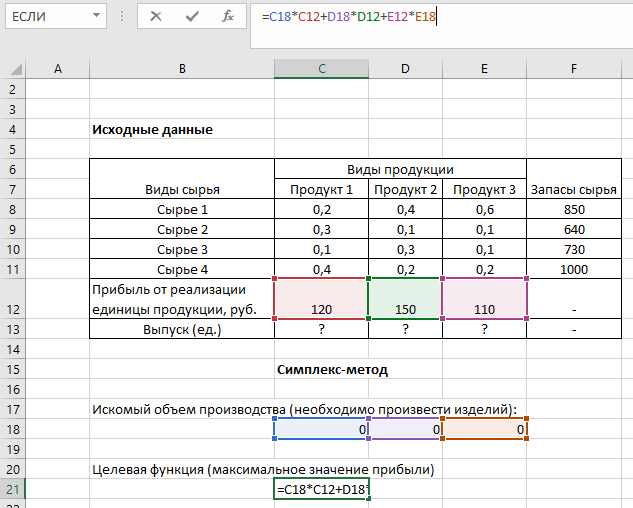Далее составим систему ограничений:


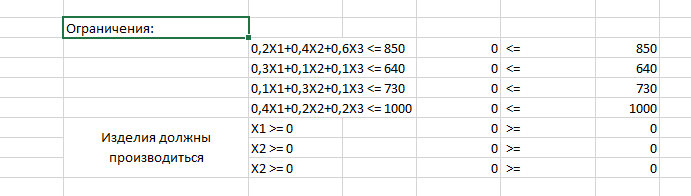Далее выбираем «Поиск решения» и дублируем обозначенные ограничения там:


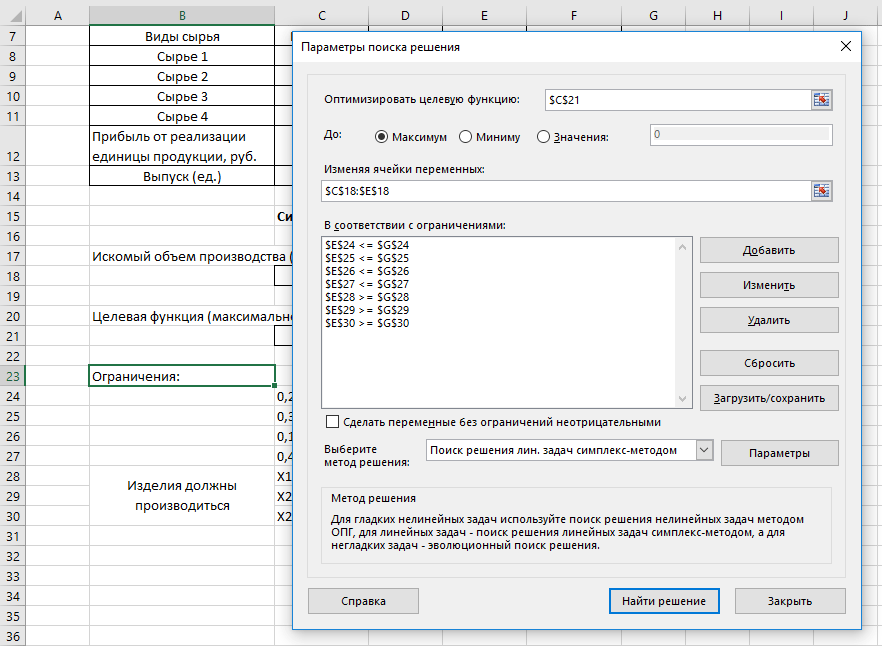Нажав кнопку «Найти решение», получаем результаты расчетов:

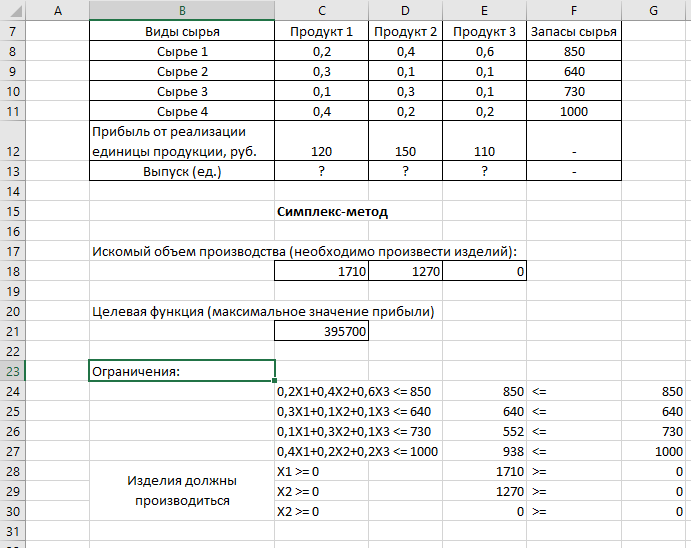Таким образом, для получения максимального объема прибыли предприятию необходимо произвести 1710 единиц Продукта №1 и 1270 единиц Продукта №2. Прибыль при этом составит 395700 руб.
№ 2. Распределить план перевозок однотипного груза от трёх поставщиков к четырём потребителям, обеспечив минимальные затраты на перевозку.

Исходные данные представлены в таблице 2.

Таблица 2. Транспортная задача.

	Тарифы по перемещению единицы груза, тыс.руб.
	Потребитель1	Потребитель2	Потребитель2	Потребитель4	Возможности поставщика
Поставщик1	7	4	9	3	400
Поставщик2	2	11	8	4	550
Поставщик 3	3	8	6	5	300
Потребности потребителя	450	250	200	350

---

Решение:
Проверим необходимое и достаточное условие разрешимости задачи:.
∑a = 400 + 550 + 300 = 1250
∑b = 450 + 250 + 200 + 350 = 1250
Условие баланса соблюдается. Запасы равны потребностям.

Следовательно, модель транспортной задачи является закрытой.
Занесем исходные данные в распределительную таблицу.

	B1	B2	B3	B4	Запасы
A1	7	4	9	3	400
A2	2	11	8	4	550
A3	3	8	6	5	300
Потребности	450	250	200	350

Этап I. Поиск первого опорного плана.
1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i, или b_j.
Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку, и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.

---

Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

Искомый элемент равен c₂₁=2. Для этого элемента запасы равны 550, потребности 450. Поскольку минимальным является 450, то вычитаем его.
x₂₁ = min(550,450) = 450.

x	4	9	3	400
2	11	8	4	550 - 450 = 100
x	8	6	5	300
450 - 450 = 0	250	200	350

Искомый элемент равен c14=3. Для этого элемента запасы равны 400, потребности 350. Поскольку минимальным является 350, то вычитаем его.
x14 = min(400,350) = 350.

x	4	9	3	400 - 350 = 50
2	11	8	x	100
x	8	6	x	300
0	250	200	350 - 350 = 0

Искомый элемент равен c12=4. Для этого элемента запасы равны 50, потребности 250. Поскольку минимальным является 50, то вычитаем его.
x12 = min(50,250) = 50.

x	4	x	3	50 - 50 = 0
2	11	8	x	100
x	8	6	x	300
0	250 - 50 = 200	200	0

---

Искомый элемент равен c33=6. Для этого элемента запасы равны 300, потребности 200. Поскольку минимальным является 200, то вычитаем его.
x33 = min(300,200) = 200.

x	4	x	3	0
2	11	x	x	100
x	8	6	x	300 - 200 = 100
0	200	200 - 200 = 0	0

Искомый элемент равен c32=8. Для этого элемента запасы равны 100, потребности 200. Поскольку минимальным является 100, то вычитаем его.
x32 = min(100,200) = 100.

x	4	x	3	0
2	11	x	x	100
x	8	6	x	100 - 100 = 0
0	200 - 100 = 100	0	0

Искомый элемент равен c22=11. Для этого элемента запасы равны 100, потребности 100. Поскольку минимальным является 100, то вычитаем его.
x22 = min(100,100) = 100.

x	4	x	3	0
2	11	x	x	100 - 100 = 0
x	8	6	x	0
0	100 - 100 = 0	0	0

---

Смотрите также файлы

• Проектирование микроволнового диодного смесителя.doc

• "Роль детской игрушки в развитии и воспитании ребенкадошкольника." по дисциплине "Теоретические основы дошкольного образования".docx

• Контрольные вопросы для самостоятельной подготовки по теме семинарского занятия 1 Общие положения об административном праве.docx

• Улучшающая инновация, т к.docx

• Тема Имущественное страхование Типовая задача 2.docx