Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Эконометрика



Группа
Студент

МОСКВА 2023

1.

1. 
   Постановочный (цели исследования, выбор показателей).
   
2. 
   Априорный (предмодельный анализ сущности явления).
   
3. 
   Параметризация (выбор модели, формы связей).
   
4. 
   Информационный (сбор статистической информации).
   
5. 
   Идентификация модели (статистическое оценивание параметров). Верификация модели (сопоставление реальных и модельных данных, оценка точности).
   
6. 
   Прогнозирование и управление.
   

2.

1) линейная y_t =a₀+a₁х_1t+...+a_nх_nt +e_t, (1.5)

2)степенная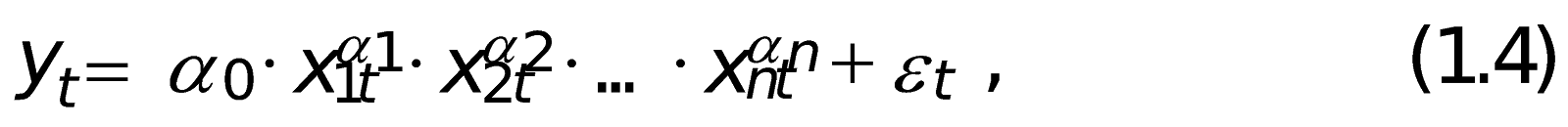

3) полулогарифмическая y_t=a₀+a₁ lnx_1t +...+a_n lnх_nt +e_t (1.6)

4) гиперболическая y_t =a₀+a₁/х_1t+...+a_n /х_nt+e_t (1.7)

5) экспоненциальная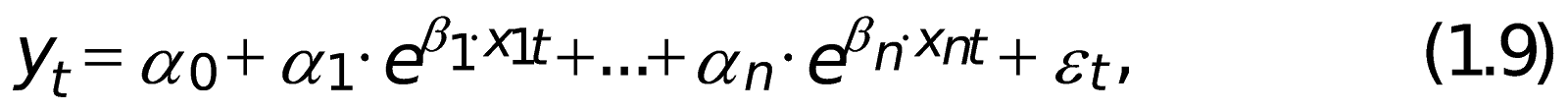

Могут применяться также комбинации рассмотренных зависимостей. 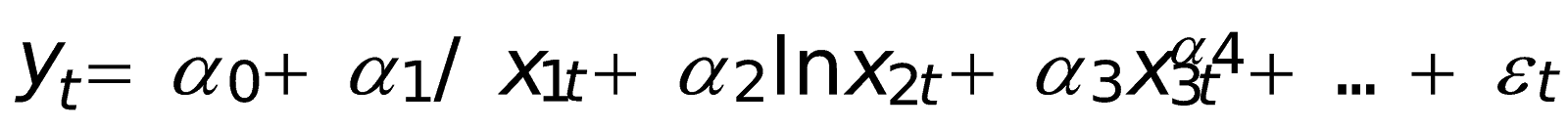Например,.

Здесь необходимо отметить, что большинство функций f(á, x_t) с помощью определенного набора преобразований могут быть приведены к линейной форме (1.5). Например, если у и х_i связаны зависимостью у

1/х_i

---

(выражение (1.7)), то, введя переменные u_i=1/х_i, получим выражение (1.4) с точностью до преобразования исходных факторов.

При выборе вида аналитической зависимости важную роль играют требования простоты модели и наличия наглядной экономической интерпретации ее параметров. Исходя из этих соображений, наиболее часто используются линейная и степенная функции.В линейной модели параметры bi при факторах хi характеризуют величину среднего изменения зависимой переменной y с изменением соответствующего фактора хi на единицу, в то время как значения остальных факторов остаются неизмененными. В степенной модели (1.4) параметры bj при факторах хi являются коэффициентами эластичности. Они показывают, на сколько процентов в среднем изменяется зависимая переменная y при изменении соответствующего фактора хi на 1 % в условиях неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.

---

Смотрите также файлы

• Приведите определения информации и дайте описание е конкретных разновидностей.pdf

• Практическое занятие 5.rtf

• Муниципальное бюджетное общеобразовательное учреждение Клюевская средняя общеобразовательная школа.docx

• эссе.docx

• Для транспорта разгазированной нефти с Хорлорского до.docx