Файл: Лабораторная работа 1 Разработка графического алгоритма решения задач по дисциплине Основы алгоритмизации и программирования 2023.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 262
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования «Алтайский государственный университет
им. И.И. Ползунова»
Университетский технологический колледж
Кафедра «Информационные системы в экономике»
Лабораторная работа №1
«Разработка графического алгоритма решения задач»
по дисциплине
«Основы алгоритмизации и программирования»
2023
Цель работы: разработать алгоритм решения задачи и представить его в графическом виде.
Задачи работы:
1 Изучить Требования Единой системы программной документации (ЕСПД) ГОСТ 19.002-80 и ГОСТ 19-003-80.
2 Повторить темы из школьной программы по математике, посвя-щённые уравнениям графиков различных функций.
3 Представить алгоритм решения уравнений в виде блок-схем.
4 Оформить отчет согласно требованиям ГОСТ 2.105-95 ЕСКД. «Общие требования к текстовым документам».
Постановка задачи:
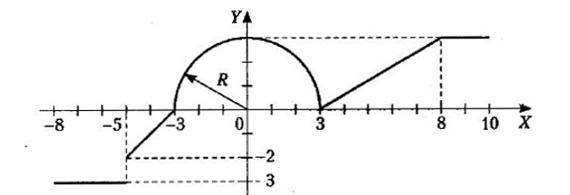
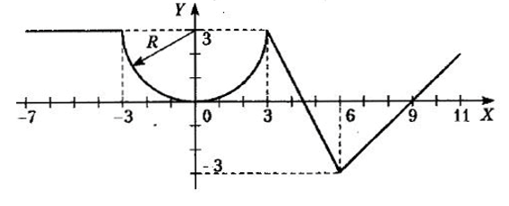
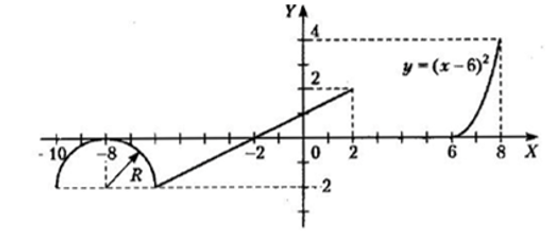
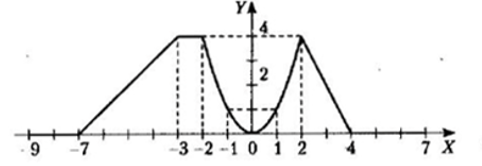
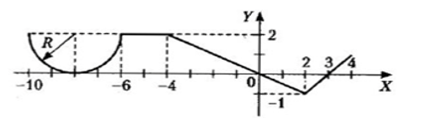
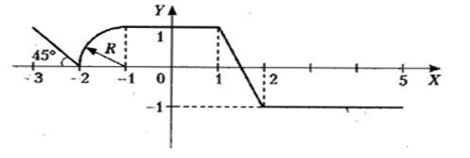
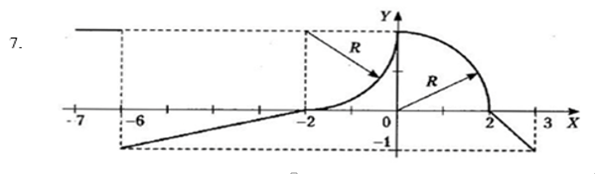
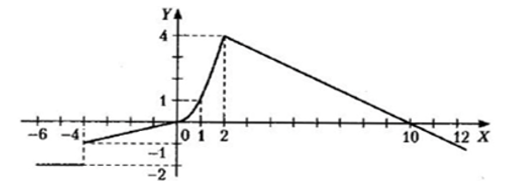
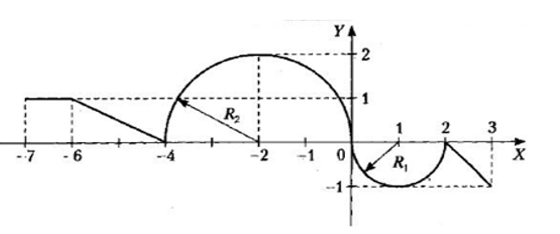
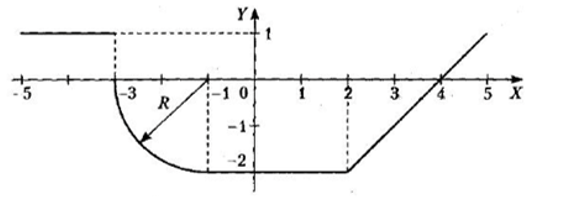
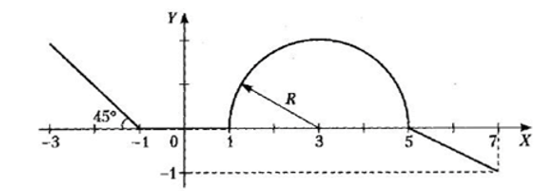
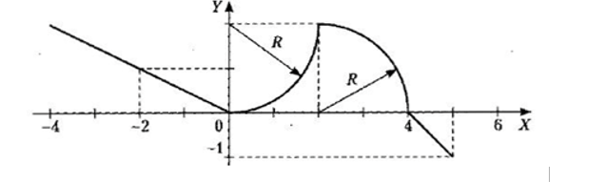
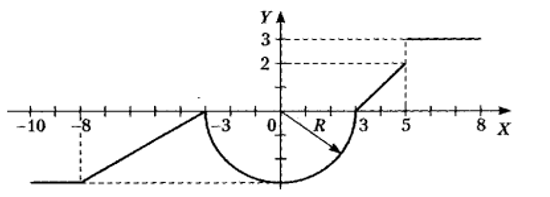
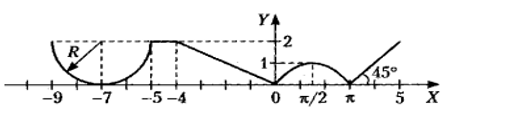
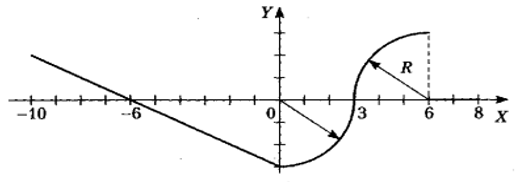
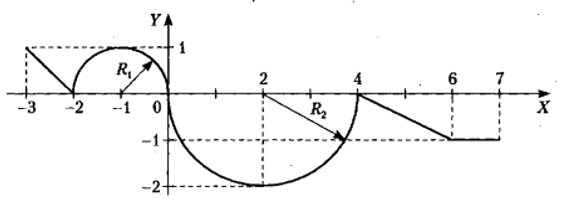
1 Для всех 18-ти комбинированных графиков на каждом из числовых интервалов, на которые разбита ось Х системы координат, найти уравнение соответствующей функции.
2 Определиться, в какие именно интервалы будут включены их крайние точки, общие для двух графиков функций.
3 Для своего варианта разработать графический алгоритм решения уравнений с учётом следующих требований:
3.1 Значение переменной Х и радиуса Rвводятся в начале алгоритма.
3.2 Алгоритм должен последовательно проверить, попадает ли введённое значение Х в какой-либо обозначенный интервал, рассчитать значение Y по соответствующей формуле и вывести его на экран.
3.3 В случае, если в разных интервалах оси Х уравнение функций одинаково, можно проверить оба условия в одном блоке.
Выполнение работы.
Для всех 18-ти комбинированных графиков на каждом из числовых интервалов, на которые разбита ось Х системы координат, найти уравнение соответствующей функции. Определиться, в какие именно интервалы будут включены их крайние точки, общие для двух графиков функций.
Для поиска уравнений следующих графиков функций будут использованы следующие базовые уравнения.
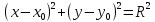- уравнение окружности, где 
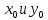– координаты центра окружности, соответственно по формуле
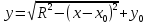получаем значение y.
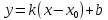– уравнение прямой, где k – коэффициент наклона, b – перемещение по оси y, 
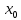– перемещение по оси x.
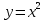– уравнение параболы 
y =
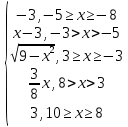
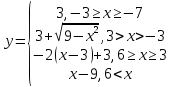
y =
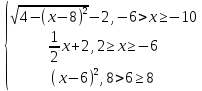
y =
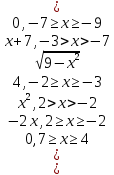
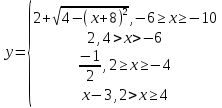
y =
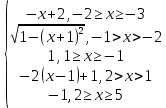
y =
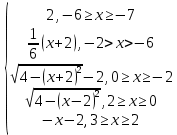
y =
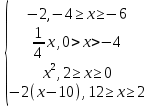
y =
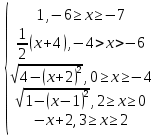
y =
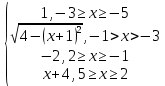
y =
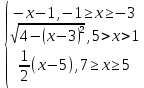
y =
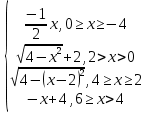
y =
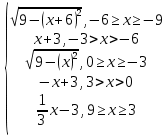
y =
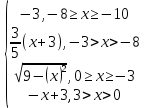
y =
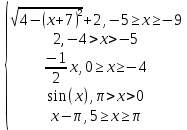
y =
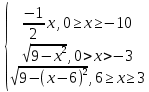
y =
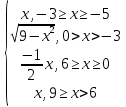
y =
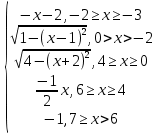
Для своего варианта разработать графический алгоритм решения уравнений с учётом следующих требований:
3.1 Значение переменной Х и радиуса Rвводятся в начале алгоритма.
3.2 Алгоритм должен последовательно проверить, попадает ли введённое значение Х в какой-либо обозначенный интервал, рассчитать значение Y по соответствующей формуле и вывести его на экран.
3.3 В случае, если в разных интервалах оси Х уравнение функций одинаково, можно проверить оба условия в одном блоке.
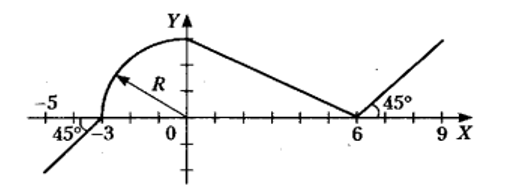
Вариант 13.
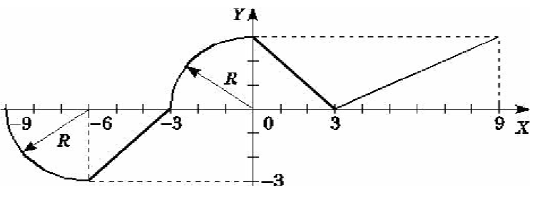
y =
Листинг кода
import math
# Ввод переменной Х и радиуса R
x = float(input("Введите значение X: "))
r = float(input("Введите значение R: "))
# Проверка, попадает ли значение Х в обозначенный интервал
if -(6+r) <= x <= -6:
# Рассчитать значение Y по соответствующей формуле
y = -math.sqrt(r*r-(x+6)*(x+6))
print("Y =", y)
elif -6 < x < -r:
y = x+3
print("Y =", y)
elif -r <= x <= 0:
y = math.sqrt(r*r-x*x)
print("Y =", y)
elif 0 < x < 3:
y = -x + 3
print("Y =", y)
elif 3 <= x <= 9:
y = (1/3)*x - 3
print("Y =", y)
else:
print("Значение Х не попадает в заданный интервал.")
Заключение
В рамках данной лабораторной работы были получены уравнения функций по графикам, а также написана программа, возвращающая значение y по введенным значениям x и радиуса окружности.
Список использованных источников
1 Поляков, К. Ю. Программирование. Python. C++. Часть 1 [Текст] : Учебное пособие / К.Ю. Поляков. – М. : БИНОМ. Лаборатория знаний, 2019. – 144 с.
2Ахмедханлы, Д. М. Основы алгоритмизации и программирования [Текст] : учеб.-метод. пособие / Д.М. Ахмедханлы, Н.В. Ушмаева. – Тольятти : Изд-во ТГУ, 2016. – 123 с.