ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 15
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
| (наименование института полностью) |
| |
| (Наименование учебного структурного подразделения) |
| |
| (код и наименование направления подготовки / специальности) |
| |
| (направленность (профиль) / специализация) |
Практическое задание № 4
по учебному курс «Высшая математика-2»
(наименование учебного курса)
Вариант 6 (при наличии)
| Обучающегося | | |
| | (И.О. Фамилия) | |
| Группа | | |
| | | |
| Преподаватель | | |
| | (И.О. Фамилия) | |
Тольятти 2023
Бланк выполнения задания 4
| № п/п | Задача | Ответ |
| 1. | Вычислить определённые интегралы. Для несобственных интегралов решить вопрос об их сходимости или расходимости: | |
| Условие задачи: а) 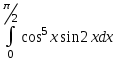 | 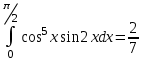 | |
| Подробное решение: 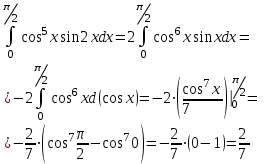 | ||
| Условие задачи: б) 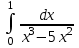 | 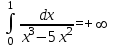 | |
| Подробное решение: При х > 0 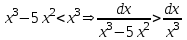 Следовательно 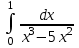 расходится по признаку сравнения с расходится по признаку сравнения с 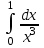 , , 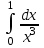 расходится, т.к. n = 3 > 1. расходится, т.к. n = 3 > 1.Проверим, вычислив 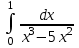 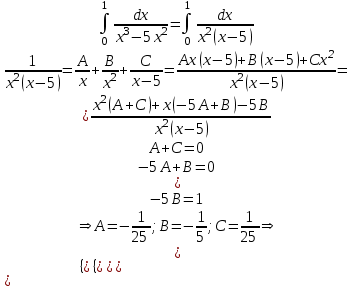 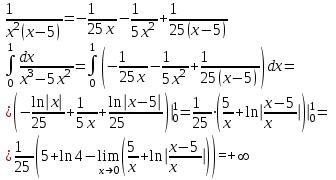 Интеграл равен конечному числу, он сходится. | ||
| Условие задачи: в) 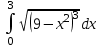 | 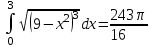 | |
| Подробное решение: 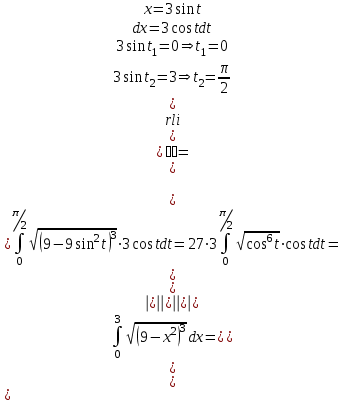 | ||
| Условие задачи: г) 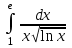 | 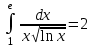 | |
| Подробное решение: 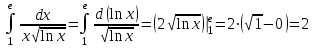 | ||
| 2. | Сделать чертеж области, ограниченной заданными линиями. Вычислить площадь полученной фигуры: | |
| Условие задачи: 2x2 - 2y = 0; 2x - 2y + 1 = 0 | S = 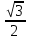 | |
| Чертёж области: 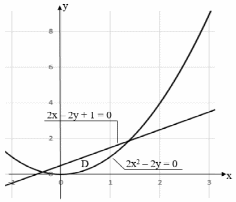 | ||
| Подробное решение: Вычислим площадь фигуры D. Определим границы интегрирования для переменной х: 2x2 - 2y = 0, у = х2; 2x – 2y + 1 = 0, у = х + 1/2; х2 = х + 1/2, х2 - х – 1/2 = 0, х1 = 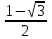 , х2 = , х2 = 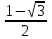 Площадь фигуры (расположена выше оси Ох): 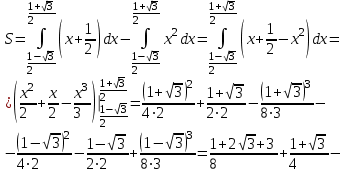 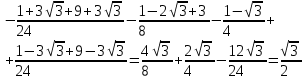 |