Файл: Контрольные вопросы Какие электрические цепи называются цепями переменного синусоидального тока.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 128
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.4. Контрольные вопросы1. Какие электрические цепи называются цепями переменного синусоидального тока? Электрические цепи, в которых значения и направления ЭДС, напряжения и тока периодически изменяются со временем по синусоидальному закону, называются цепями синусоидального тока. Иногда их называют просто цепями переменного тока.Для переменного тока была выбрана синусоидальная форма, так как она обеспечивает более экономичные производство, передачу, распределение и использование электрической энергии.2. Опишите процесс получения синусоидальных сигналов. U1 & U2 & U3 & 1 I & 2 I & 3 I & + j +1 0 48.Каждый параметр режима электрической цепи (i, u, e) изменяется по синусоидальному закону:Где f(t) – мгновенное значение функции; Am – амплитуда функции; ω – угловая частота; Ψ – начальный фазный угол.Аргумент синусоидальной функции – фазовый угол или фаза. В момент времениt = 0 значение фазового угла называют начальной фазой. Аргумент синусоидальной функции может выражаться в градусах или радианах.3. Какие характеристики синусоидальных сигналов Вы знаете? Синусоидальный сигнал - - простейший вид сигнала. И характеристик у него всего три. Амплитуда, частота и фаза. Притом фазу можно указать только относительно какого-то другого сигнала той же частоты. Так что у изолированного сигнала будет только две характеристики - - амплитуда и частота. Синусоидальный ток – это переменный ток, мгновенное значение которого изменяется с течением времени по закону синуса или косинуса – U (t)=Ua sin (wt+фи)4. В чем заключается расчет электрической цепи переменного синусоидального тока методом комплексных амплитуд? Сущность метода состоит в том, что синусоидальные токи, напряжения и ЭДС изображаются комплексными числами, а геометрические операции над векторами заменяются алгебраическими операциями над комплексными числами. Этот метод позволяет рассчитывать цепи синусоидального тока алгебраически аналогично цепям постоянного тока.5. Как выполняется переход от комплексной амплитуды тока к его мгновенному значению? Мгновенное значение величины, а показывает закон ее изменения и записывается в виде:А = Аm sin(ωt +ψ ),Где Аm – амплитуда (максимальное значение) величины;Ω- угловая частота, рад/с;T– текущее значение времени, с;Ψ – начальная фаза.Мгновенные значения тока i , напряжения u или ЭДС e записываются в виде:
I = Im sin(ωt +ψi ),U =U m sin(ωt +ψu )E = Em sin(ωt +ψe ).Аргумент синуса (ωt +ψ ) называется фазой. Угол ψ равен фазе в начальный момент времени t =0 и поэтому называется начальной фазой.Угловая частота ω связана с периодом T и частотой f = 12πΩ =Или ω = 2πf ,Частота f, равная числу колебаний в 1с., измеряется в герцах (Гц). ПриF=50 Гц имеем ω =314 рад/с.Сучетом (3.5) формула (3.1) может иметь вид:I1 = Im1 sin(ωt +ψ1 ); i2 = Im2 sin(ωt +ψ2 ).6. Какие идеальные элементы схем замещения электрических цепей используются для описания процессов, происходящих в реальных электрических цепях? Чтобы описать динамическое состояние реальной цепи необходимо в каждой ветви установить связь между напряжением и током, которая может быть довольно сложной. Для упрощения описания в теории электрических цепей вводится понятие идеальных элементов цепи. Связь между напряжением и током на них вводятся формально на основании законов электромагнетизма.7. Запишите уравнение резистивного элемента. Какой сдвиг фаз вносит резистивный элемент между напряжением и током? Резистивный элемент. Пусть к зажимам резистивного элемента (рис.3.4а) приложено синусоидальное напряжение . а бРисунок 3.4 — Резистивный элемент в цепи синусоидального тока и его ЧХВ соответствии с законом Ома переменный ток, проходящий через резистивный элемент, определяется как , причем .Полученное выражение означает, что:врезистивной цепи синусоиды тока и напряжения одинаковы по частоте и совпадают по фазе. Таким образом,на резистивном элементе не образуется сдвиг фаз между током и напряжением. Активное сопротивление
не зависит от частоты сигнала (рис.3.4б).Мгновенная мощность, передаваемая от источника к резистивному элементу, определяется какили .Из полученного выражения следует
до , колеблясь вокруг среднего значения . 9. Запишите уравнение емкостного элемента. Какой сдвиг фаз вносит емкостной элемент между напряжением и током? Пусть к емкостному элементу (рис.3.6а) приложено синусоидальное напряжение . Тогда ток через емкостной элемент определяется как , где .а бПолученное выражение означает, что:вцепи с емкостным элнментом синусоида тока опережает синусоиду напряжения на
. Таким образом,на емкостном элементе образуется сдвиг фаз между током и напряжением. Если сравнить полученное выражение с записью закона Ома, то сомножитель будет иметь размерность проводимости. Обратная величина называется емкостным сопротивлением. Емкостное сопротивление 
обратно пропорционально частоте сигнала (рис.3.6б).Мгновенная мощность, передаваемая от источника к емкостному элементу, определяется как .Из полученного выражения следует, что мгновенная мощность цепи с емкостным элементом может быть как положительной, так и отрицательной величиной, т.е. при возрастании напряжения энергия емкостном элементе накапливается, т.е. конденсатор заряжается. При убывании накопленная энергия возвращается в цепь. 10. Как определяется полное комплексное сопротивление электрической цепи? Пассивный элемент в цепи синусоидального тока определяется своим комплексным сопротивлением
,где — вещественная часть комплексного сопротивления, равная активному сопротивлению цепи; — мнимая часть комплексного сопротивления, равная реактивному сопротивлению цепи; — модуль комплексного сопротивления цепи, равен ; — аргумент комплексного сопротивления, равный углу сдвига фаз между током и напряжением, .Комплексное сопротивление определяется как отношение комплексного напряжения к комплексному току : .Комплексные сопротивления отдельных пассивных элементов приведены в табл.3.2. Для резистивного элемента комплексное сопротивление является чисто активным, а для индуктивного и емкостного — чисто реактивным. 11. Как определяется полная комплексная проводимость электрической цепи? Связь между комплексным сопротивлением и проводимостью. Установим соответствие между величинами комплексного сопротивления и проводимости: ; ; ; ; ; .Мощность в линейной
-цепи синусоидального тока. Для цепи с напряжением на участке цепи и током полная мощность в комплексной форме определяется следующим образом:
I = Im sin(ωt +ψi ),U =U m sin(ωt +ψu )E = Em sin(ωt +ψe ).Аргумент синуса (ωt +ψ ) называется фазой. Угол ψ равен фазе в начальный момент времени t =0 и поэтому называется начальной фазой.Угловая частота ω связана с периодом T и частотой f = 12πΩ =Или ω = 2πf ,Частота f, равная числу колебаний в 1с., измеряется в герцах (Гц). ПриF=50 Гц имеем ω =314 рад/с.Сучетом (3.5) формула (3.1) может иметь вид:I1 = Im1 sin(ωt +ψ1 ); i2 = Im2 sin(ωt +ψ2 ).6. Какие идеальные элементы схем замещения электрических цепей используются для описания процессов, происходящих в реальных электрических цепях? Чтобы описать динамическое состояние реальной цепи необходимо в каждой ветви установить связь между напряжением и током, которая может быть довольно сложной. Для упрощения описания в теории электрических цепей вводится понятие идеальных элементов цепи. Связь между напряжением и током на них вводятся формально на основании законов электромагнетизма.7. Запишите уравнение резистивного элемента. Какой сдвиг фаз вносит резистивный элемент между напряжением и током? Резистивный элемент. Пусть к зажимам резистивного элемента (рис.3.4а) приложено синусоидальное напряжение 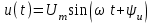. 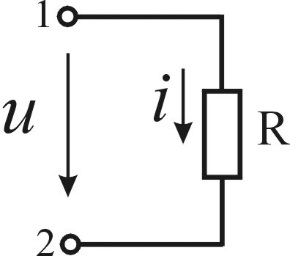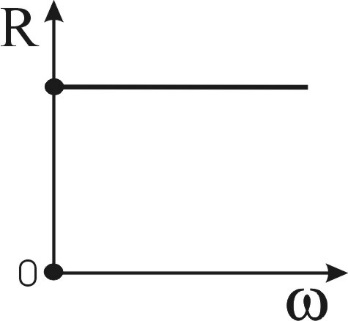а бРисунок 3.4 — Резистивный элемент в цепи синусоидального тока и его ЧХВ соответствии с законом Ома переменный ток, проходящий через резистивный элемент, определяется как 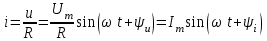, причем 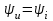.Полученное выражение означает, что:врезистивной цепи синусоиды тока и напряжения одинаковы по частоте и совпадают по фазе. Таким образом,на резистивном элементе не образуется сдвиг фаз между током и напряжением. Активное сопротивление
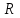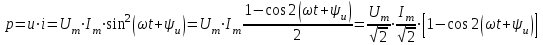
не зависит от частоты сигнала (рис.3.4б).Мгновенная мощность, передаваемая от источника к резистивному элементу, определяется какили 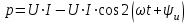.Из полученного выражения следует
, мгновенная мощность цепи с резистивным элементом всегда положительна, т.е. энергия только потребляется, превращаясь в тепло. Значение мгновенной мощности изменяется периодически от 0 до 
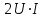, колеблясь вокруг среднего значения 
.
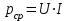8. Запишите уравнение индуктивного элемента. Какой сдвиг фаз вносит индуктивный элемент между напряжением и током?
Пусть через индуктивный элемент (рис.3.5а) протекает синусоидальный ток 
. 
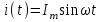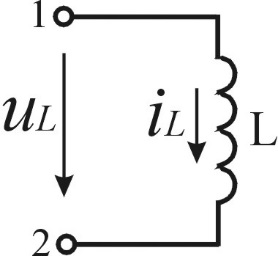
а б
Рисунок 3.5 — Индуктивный элемент в цепи синусоидального тока и его ЧХ
На основании закона электромагнитной индукции напряжение на индуктивном элементе определяется как
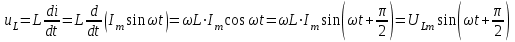, где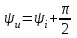 
.
Полученное выражение означает, что:
в цепи с индуктивным элементом синусоида напряжения опережает синусоиду тока на 
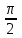. Таким образом, на индуктивном элементе образуется сдвиг фаз между током и напряжением.
Если сравнить полученное выражение с записью закона Ома, то сомножитель 
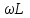будет иметь размерность сопротивления. Величина 
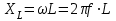называется индуктивным сопротивлением, которое учитывает влияние ЭДС самоиндукции в цепи.
Индуктивное сопротивление 
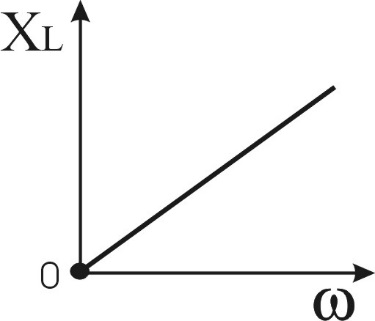
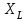линейно зависит от частоты сигнала (рис.3.5б).
Мгновенная мощность, передаваемая от источника к индуктивному элементу, определяется как
.
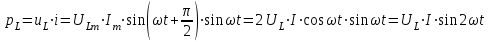Из полученного выражения следует, что мгновенная мощность цепи с индуктивным элементом может быть как положительной, так и отрицательной величиной, т.е. при возрастании тока энергия магнитного поля в индуктивном элементе накапливается, а при убывании тока энергия возвращается в цепь. Значение мгновенной мощности изменяется периодически от
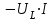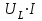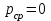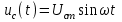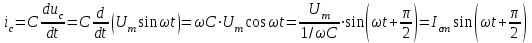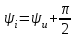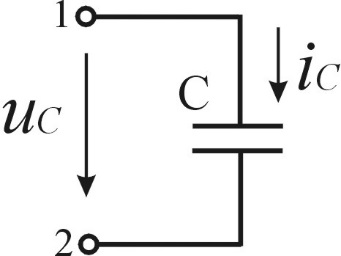
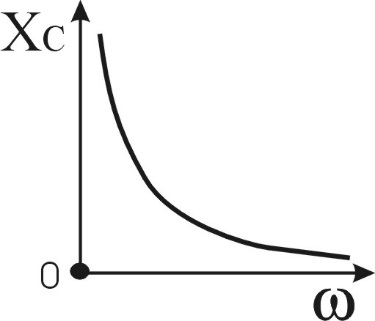
до , колеблясь вокруг среднего значения . 9. Запишите уравнение емкостного элемента. Какой сдвиг фаз вносит емкостной элемент между напряжением и током? Пусть к емкостному элементу (рис.3.6а) приложено синусоидальное напряжение . Тогда ток через емкостной элемент определяется как , где .а бПолученное выражение означает, что:вцепи с емкостным элнментом синусоида тока опережает синусоиду напряжения на
. Таким образом,на емкостном элементе образуется сдвиг фаз между током и напряжением. Если сравнить полученное выражение с записью закона Ома, то сомножитель 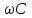будет иметь размерность проводимости. Обратная величина 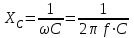называется емкостным сопротивлением. Емкостное сопротивление 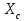обратно пропорционально частоте сигнала (рис.3.6б).Мгновенная мощность, передаваемая от источника к емкостному элементу, определяется как 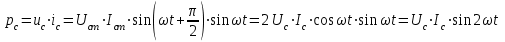.Из полученного выражения следует, что мгновенная мощность цепи с емкостным элементом может быть как положительной, так и отрицательной величиной, т.е. при возрастании напряжения 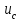энергия емкостном элементе накапливается, т.е. конденсатор заряжается. При убывании 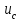накопленная энергия возвращается в цепь. 10. Как определяется полное комплексное сопротивление электрической цепи? Пассивный элемент в цепи синусоидального тока определяется своим комплексным сопротивлением
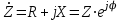,где — вещественная часть комплексного сопротивления, равная активному сопротивлению цепи;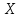 — мнимая часть комплексного сопротивления, равная реактивному сопротивлению цепи; 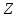— модуль комплексного сопротивления цепи, равен 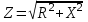; 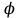— аргумент комплексного сопротивления, равный углу сдвига фаз между током и напряжением, 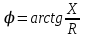.Комплексное сопротивление определяется как отношение комплексного напряжения к комплексному току : 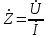.Комплексные сопротивления отдельных пассивных элементов приведены в табл.3.2. Для резистивного элемента комплексное сопротивление 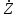является чисто активным, а для индуктивного и емкостного — чисто реактивным. 11. Как определяется полная комплексная проводимость электрической цепи? Связь между комплексным сопротивлением и проводимостью. Установим соответствие между величинами комплексного сопротивления и проводимости: 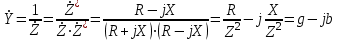; ; 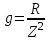; ; 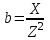; 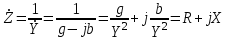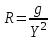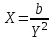.Мощность в линейной
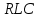-цепи синусоидального тока. Для цепи с напряжением на участке цепи 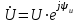и током 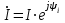полная мощность в комплексной форме определяется следующим образом: