Файл: Решение Перепишем систему в векторноматричной форме.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 13
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решить систему методом Ньютона:
| № | Система уравнений | Точность |
| 12 | 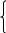 14 14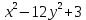 =0 =02x+ 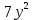 -9=0 -9=0 | 0.0001 |
Решение:
Перепишем систему в векторно-матричной форме:
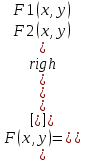
Запишем итерационную формулу метода Ньютона:
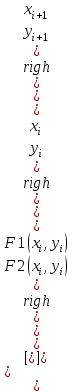
и перепишем ее, переходя от вычисления обратной матрицы к решению системы линейных алгебраических уравнений:
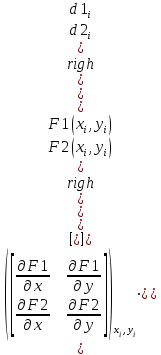 ;
;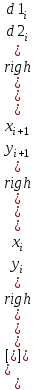 .
.Таким образом, на каждой итерации надо вычислить якобиан и функцию F, решить возникшую систему линейных алгебраических уравнений (например, методом Крамера) относительно [d1i; d2i]T и по ним найти xi+1, yi+1. Итерации закончатся, когда квадрат нормы вектора приращений переменных станет меньше заданной точности.
Решение на Паскале:
Program task3; { Решение системы методом Ньютона }
Const EPS = 0.0001; { Точность расчета }
{ Процедура, вычисляющая первую и вторую функции системы [ F1(X,Y) = 0; F2(X,Y) = 0 ] }
Procedure F(X, Y: Real; Var F1, F2: Real);
Begin
F1 := 14.0*X*X - 12.0*Y*Y + 3.0;
F2 := 2.0*X + 7.0*Y*Y - 9.0
End;
{ Процедура, вычисляющая якобиан системы функций [ F1(X,Y) = 0; F2(X,Y) = 0 ] }
{ Результатом является матрица = [ dF1/dX dF1/dY ] = [ G11 G12 ] }
{ [ dF2/dX dF2/dY ] [ G21 G22 ] }
Procedure G(X, Y: Real; Var G11, G12, G21, G22: Real);
Begin
G11 := 28.0*X;
G12 := -24.0*Y;
G21 := 2.0;
G22 := 14.0*Y
End;
{ Процедура, реашющая систему линейных уравнений методом Крамера: }
{ A1*X1 + B1*X2 = C1 }
{ A2*X2 + B2*X2 = C2 }
Procedure Solve(A1, B1, C1, A2, B2, C2: Real; Var X1, X2: Real);
Var D: Real; { Определитель системы }
Begin
D := A1*B2 - A2*B1;
X1 := (C1*B2 - C2*B1)/D;
X2 := (A1*C2 - A2*C1)/D
End;
Var X0, Y0: Real; { Предыдущая точка решения }
X1, Y1: Real; { Следующая точка решения }
D1, D2: Real; { Приращения X и Y }
F1, F2: Real; { Значения функций системы }
G11, G12, G21, G22: Real; { Компоненты якобиана }
k: Integer; { Число итераций }
D: Real; { Невязка }
Begin
{ Ввод исходных данных }
WriteLn('Vvedite nachalnuyu tochku:');
Write('X0 = '); ReadLn(X0);
Write('Y0 = '); ReadLn(Y0);
k := 1;
F(X0, Y0, F1, F2); { Вычисляем функции системы }
D1 := 0.0; D2 := 0.0;
Repeat { Цикл расчета }
G(X0, Y0, G11, G12, G21, G22); { Вычисляем градиент }
Solve(G11, G12, -F1, G21, G22, -F2, D1, D2); { Находим приращения, решая систему Jacobian*D = -F, что }
{ эквивалентно нахождению D = (Jacobian^(-1))*(-F) }
X1 := X0 + D1;
Y1 := Y0 + D2;
F(X1, Y1, F1, F2); { Вычисляем функции системы }
WriteLn(k:2, '. X = ', X1:8:5, ' : Y = ', Y1:8:5);
WriteLn(' F1(X,Y) = ', F1:8:5, ' : F2(X,Y) = ', F2:8:5);
D := D1*D1 + D2*D2;
WriteLn(' Nevyazka = ', D:8:5);
X0 := X1;
Y0 := Y1;
Inc(k);
Until D <= EPS; // Пока невязка не станет меньше точности расчета
ReadLn
End.
Результат (скриншоты):
Обнаружилось, что система имеет четыре решения, которые удалось получить, изменяя начальную точку.
Первое решение:

Второе решение:
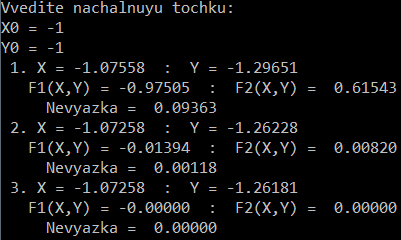
Третье решение:
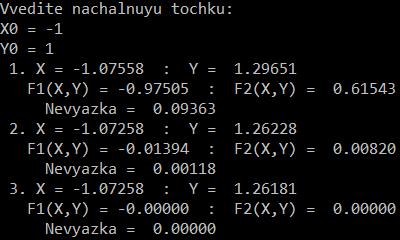
Четвертое решение: