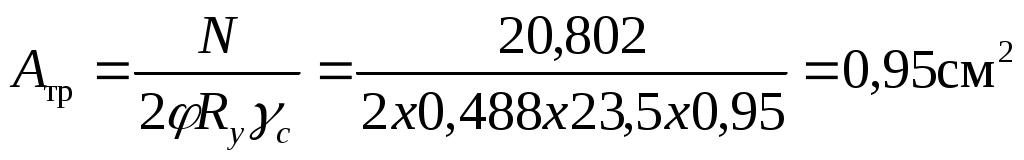
: N=20,802 кН; l=4,208 мПлощадь сечения верхнего сжатого пояса определяют по формуле (1). 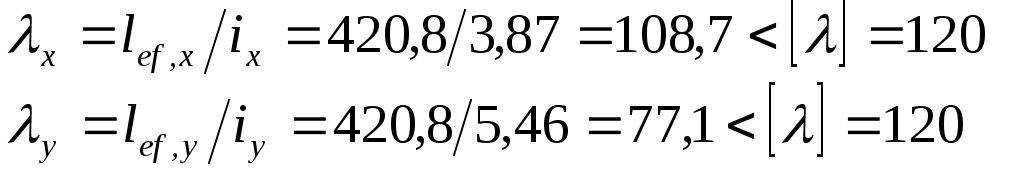Принимаем ƛ=????√R_y/E=100√23,5/20*10³=3,43По таблице Д1 СП16.13330-2017, принимаемφ=0,488Требуемая площадь сечения одного уголкаОпределим требуемые радиусы инерции: =0,8*420,8/100=3,37 см = 420,8/100=4,2 см Из сортамента находим равнополочные уголки 125х8, А =19,69 см²., радиусы инерции сечения верхнего пояса равны: i_x= 3,87 см; i_y= 5,46 см.Гибкости стержнягде [ λ ] = [120] – предельная гибкость (СП16.13330-2017 )Проверка устойчивости стержня.Проверка устойчивости стержня проводим по наименьшему значению коэффициента φ_х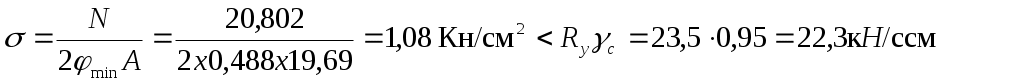Устойчивость стержня обеспечена.Подбираем сечение сжатой стойки 0-1: N=52,005 кН; l=2,20 мПлощадь сечения верхнего сжатого пояса определяют по формуле (1). 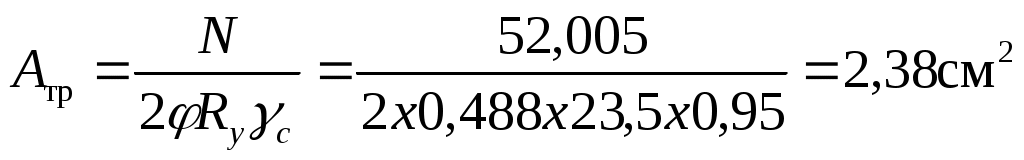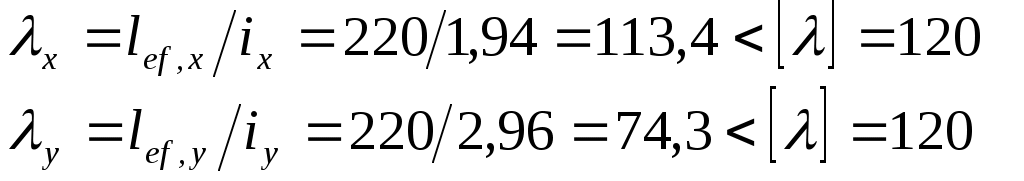Принимаем ƛ=????√R_y/E=100√23,5/20*10³=3,43По таблице Д1 СП16.13330-2017, принимаемφ=0,488Требуемая площадь сечения одного уголкаОпределим требуемые радиусы инерции: =0,8*220/100=1,76 см = 220/100=2,2 см Из сортамента находим равнополочные уголки 63х5, А =6,13 см²., радиусы инерции сечения верхнего пояса равны: i_x= 1,94 см; i_y= 2,96 см.Гибкости стержнягде [ λ ] = [120] – предельная гибкость (СП16.13330-2017 )Проверка устойчивости стержня.Проверка устойчивости стержня проводим по наименьшему значению коэффициента φ_х

---

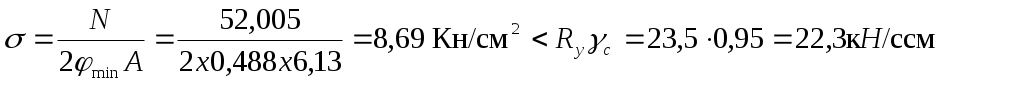
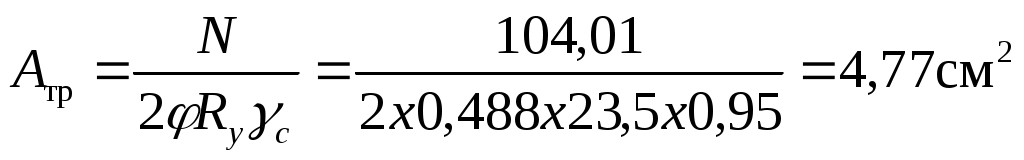
Устойчивость стержня обеспечена.Подбираем сечение сжатой стойки 3-4: N=104,01 кН; l=2,70 мПлощадь сечения верхнего сжатого пояса определяют по формуле (1). 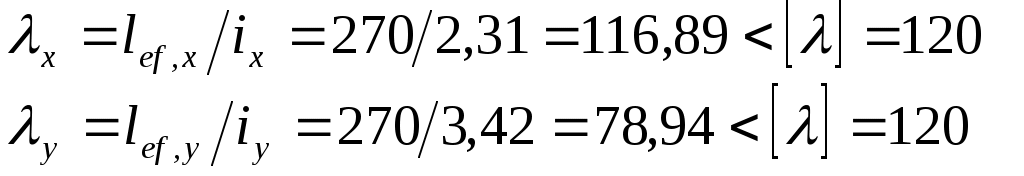Принимаем ƛ=????√R_y/E=100√23,5/20*10³=3,43По таблице Д1 СП16.13330-2017, принимаемφ=0,488Требуемая площадь сечения одного уголкаОпределим требуемые радиусы инерции: =0,8*270/100= 2,16 см = 270/100=2,7 см Из сортамента находим равнополочные уголки 75х5, А =7,39 см²., радиусы инерции сечения верхнего пояса равны: i_x= 2,31 см; i_y= 3,42 см.Гибкости стержнягде [ λ ] = [120] – предельная гибкость (СП16.13330-2017 )Проверка устойчивости стержня.Проверка устойчивости стержня проводим по наименьшему значению коэффициента φ_х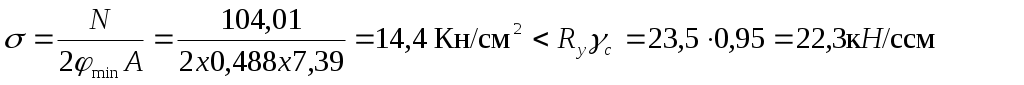Подбираем сечение растянутой стойки 6-7: N=31,203 кН; l=3,2мТребуемая площадь сечения одного уголка при _с=0,95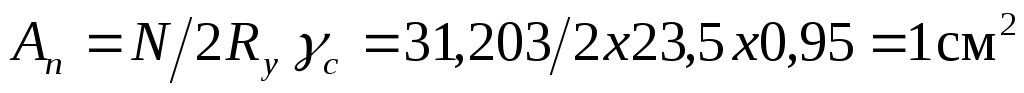По сортаменту находим равнополочные уголки 63х5; А=6,13 см²; i_x=1,94см; i_y=2,96 см.Расчетная длина: l_x=6м – расстояние между смежными узлами фермы;l_y=6м – расстояние между узлами связей по нижнему поясу.Гибкость элемента;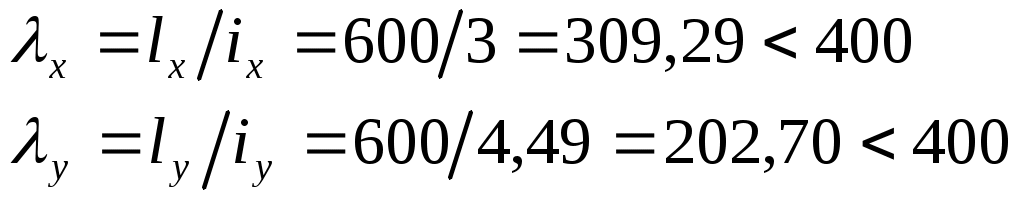Устойчивость стержня обеспечена.Расчет сварных швов узла 1Расчет сварного соединения с угловыми швами при действии силы N, проходящего через центр тяжести соединений, следует выполнять на срез (условный) по одному из двух сечений по формулам: при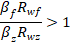 по металлу шва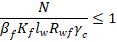 при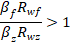

---

по металлу границы сплавления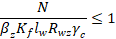

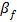-при катете шва 3-8-1,1; 9-12-0,9

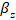-при катет шва 3-8-1,15; -12-1,05

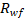-расчетное сопротивление срезу по металлу шва

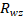-расчетное сопротивление по металлу границы сплавления
При электроде Э50 и марке проволоки Св-08Г2С -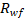 =215Н/мм²;

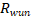=490 Н/мм²,

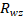=0,45* 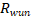=0,45*400 (по таблице С16)=180 мПа

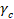=0,8 (по таблице СП16)
Определяем сварной шов сжатого раскоса 4-5: N=145,614 кН



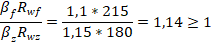
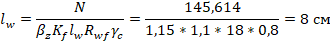
Определяем сварной шов растянутого раскоса 2-3: N=322,431 кН



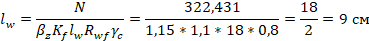
Определяем сварной шов сжатой стойки 3-4: N=104,01 кН


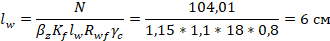
Вывод:

Верхний пояс-2 уголка 160х11

Нижний пояс- 2 уголка 110х10

Стойки (0-1; 6-7)-2 уголка 63х5

(3-4)-2 уголка 75х5

Раскосы (1-2)-2 уголка 160х11

(2-3)-2 уголка 70х5

(4-5; 5-6)- 2 уголка 125х8

---

Смотрите также файлы

• Готфрид Вильгельм Лейбниц Джон Локк Дэвид Юм Джордж Беркли Т. Гоббс Бенедикт Спиноза Его трактат О душе первое специальнопсихологическое сочинение.docx

• Ассортимент приготовления и способы реализации горячих блюд для гриль бар.docx

• Текст вопроса Предметом бухгалтерского учета является a.docx

• Тест по темам Грамматика как раздел науки о языке, Морфология как раздел грамматики.doc

• Курсовая работа по дисциплине Управление в чрезвычайных ситуациях на тему Возможные экономические, социальные и экологические последствия чрезвычайных ситуаций.docx