Объёмные тела.Тела вращения.

Работу выполнила:
ученик класса

СОДЕРЖАНИЕ

ВВЕДЕНИЕ……………………………………………………………….........

1. Тела вращения, основы и способы их образования……………..

2. Вычисление объемов тел вращения различными способами…...

3. Принцип Кавальери……………………………………………….

4.Практическое применение…………………………………………

4.1 Задачи на объёмные тела………………………………………..

4.2 Объёмные тела в архитектуре…………………………………..

ЗАКЛЮЧЕНИЕ…………………………………………………………………

СПИСОК ЛИТЕРАТУРЫ…………...…………………………………….........



Пояснительная записка

Геометрия - удивительная наука. Задачи, включающие в себя решение и разбор тем по телам вращения меня очень заинтересовали и я постаралась в них разобраться. Решение задач на тела вращения требует глубокого проникновения в смысл условия задачи. Также, в экзаменационных вариантах единого государственного экзамена (ЕГЭ) содержатся вопросы, которые связанны с фигурами вращения, и чтобы решить их, нужно знать теоретический материал. Четкое сопоставление формул, теорем и их доказательств играет главную роль в решении таких задач.

Тема моей работы звучит так: «Объёмные тела. Тела вращения».

Объектом исследования являются - Тела вращения и применение их в архитектуре.

Цель работы:

- Исследование тел вращения. Применение их в архитектуре.

Задачи:

- формировать навыки самостоятельной работы с различными источниками информации;

- углубить и расширить знания о нахождении площадей и объемов тел вращения

- рассмотреть тела вращения на примере сооружений и архитектурных зданий.

Актуальность: расширить свои знания о телах вращения.

План исследования:

- Узнать историю изучения тел вращения.

- Научиться применять формулы, теоремы при решении задач.

- Сделать выводы.

Объект исследования – Тела вращения.

Предмет исследования – Задачи по теме «Тела вращения».

---

Цель исследования – Систематизация теоретического материала и его применение к решению задач.

Введение

Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности - от двухлетнего ребёнка, играющего деревянными кубиками, до зрелого математика. Особый интерес к многоугольникам и многогранникам связан с красотой и совершенством формы. Они довольно часто встречаются в природе. Достаточно вспомнить форму снежинок, граней кристаллов, ячеек в пчелиных сотах. Эта тема выбрана потому, что понятие многогранника является одним из центральных в курсе стереометрии. Многогранники интересны и сами по себе. Они имеют красивые формы. Формы многогранников находят широкое применение в конструировании сложных и красивых многогранных поверхностей, которые используются в реальных архитектурных проектах. Идёт это с глубокой древности. Пирамида - это норма тектоники - внутреннего устройства каменных зданий прошлого. (В частности пирамида Хеопса, имеют форму многогранников). Силуэты каменных церквей и соборов, как правило, вписываются в форму пирамиды. «Только неотступно следуя законам геометрии, архитекторы древности могли создать свои шедевры. Не случайно говорят, что пирамида Хеопса - немой трактат по геометрии, а греческая архитектура - внешнее выражение геометрии Евклида. «Прошли века, но роль геометрии не изменилась. Она по-прежнему остаётся грамматикой архитектора» - это высказывание принадлежит великому французскому архитектору Ле Корбюзье. (1887-1965). Поэтому захотелось больше узнать о многогранниках.

Для продуктивной деятельности в современном информационном мире требуется достаточно прочная базовая математическая подготовка, поэтому изучение темы «Объемы многогранников» очень актуально, так как они необходимы для изучения смежных дисциплин, для продолжения образования. Тема «Объемы » - одна из центральных тем в курсе стереометрии средней школы. Проблема организации уроков по изучению объемов многогранников одна из самых актуальных, так как она занимает значительную часть в курсе стереометрии. Во всяком подлинно геометрическом предложении, будь то аксиома, теорема или определение, неразрывно присутствуют эти два элемента: наглядная картина и строгая формулировка, строгий логический вывод. Там, где нет ни одной из двух сторон, нет и подлинной геометрии. Именно при изучении многогранников и их объемов решение данной задачи выступает наиболее ярко, и их рассмотрению должно быть уделено больше внимания, потому что многогранники дают особенно богатый материал для развития пространственных представлений, для развития того соединения живого пространственного воображения со строгой логикой, которая составляет сущность геометрии.

---

1. Тела вращения, основы и способы их образования

Тела вращения – это объёмные фигуры, которые так или иначе связаны с окружностью и кругом.

У каждого тела вращения есть оси, относительно которых они симметричны. Рассмотрим три тела вращения подробнее: цилиндр, конус и шар.



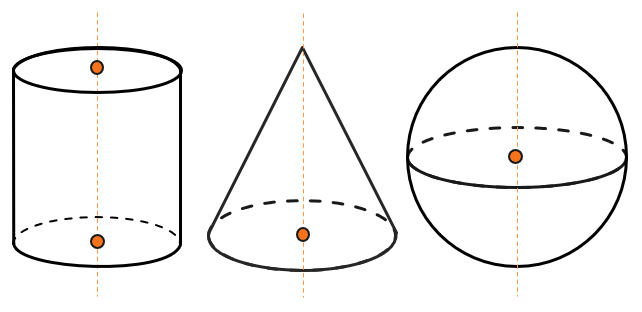
Цилиндр – это фигура, похожая на призму, с разницей лишь в том, что у нее в основаниях вместо многоугольников – окружность. Получается, что у такой фигуры нет боковых граней в виде многоугольников, а есть только она сплошная грань:



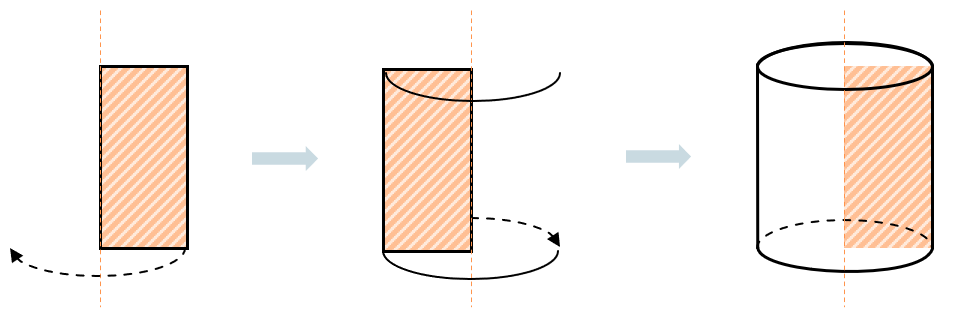
Цилиндр можно «образовать», если прокрутить прямоугольник вокруг одной из его сторон. Эта сторона прямоугольника станет осью будущего цилиндра:



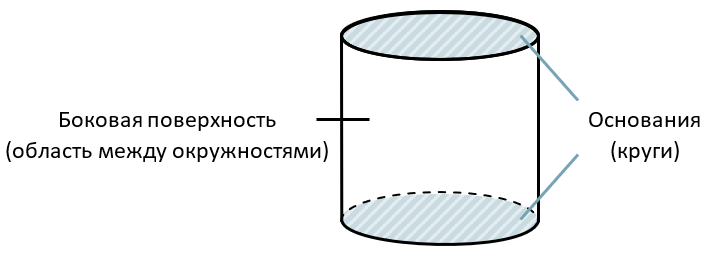
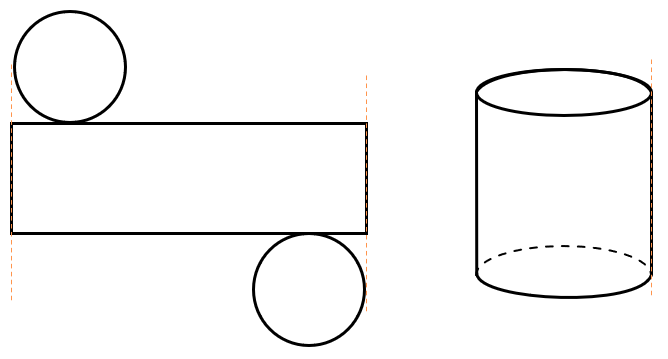
Разверткой цилиндра является прямоугольник (боковая поверхность цилиндра) и две окружности (его основания):



Конус – это тело вращения, похожее на пирамиду. У него есть основание и вершина, только вместо многоугольника в основании окружность, поэтому у нее тоже одна боковая грань:



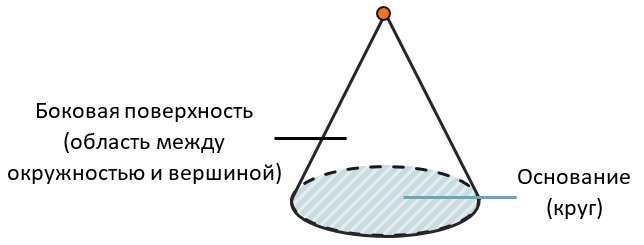
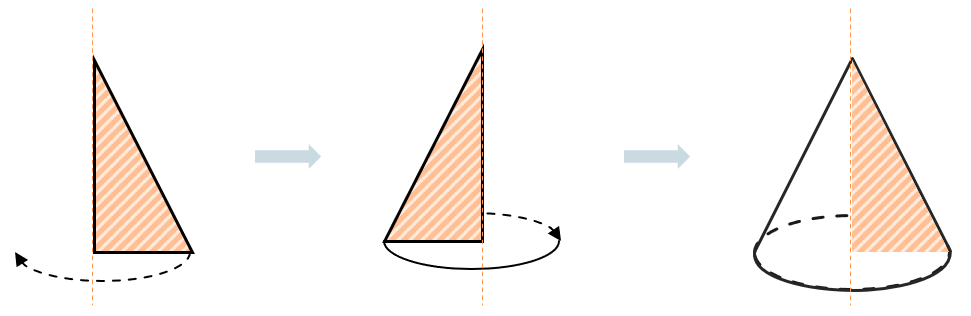
Конус можно «образовать» вращением прямоугольного треугольника вокруг его стороны, которая станет осью для будущего конуса:



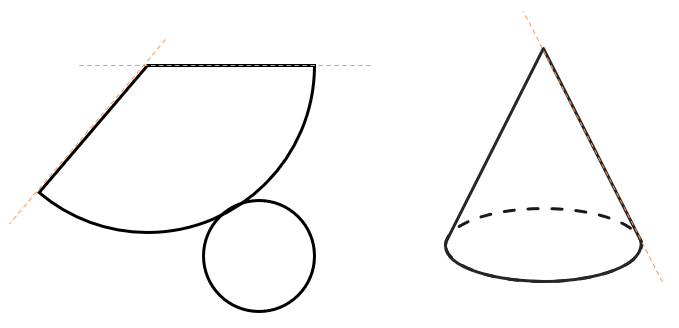
Развертка конуса – это часть большой окружности (боковая поверхность) и окружность поменьше (основание конуса):



Шар – это фигура, которая абсолютная симметричная своей точке – центру.

Шар выглядит как мяч или капля воды в воздухе. У шара нет оснований и граней. У него есть только сфера – поверхность шара. Любая точка на сфере удалена от центра шара на радиус r.

---

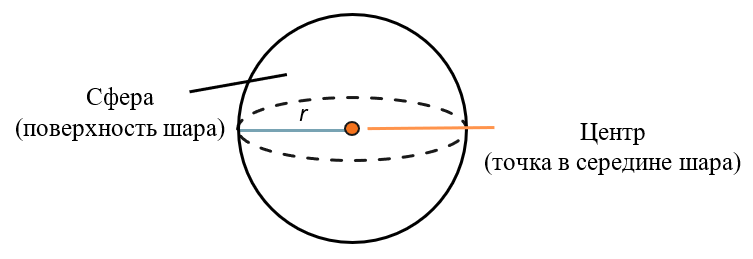
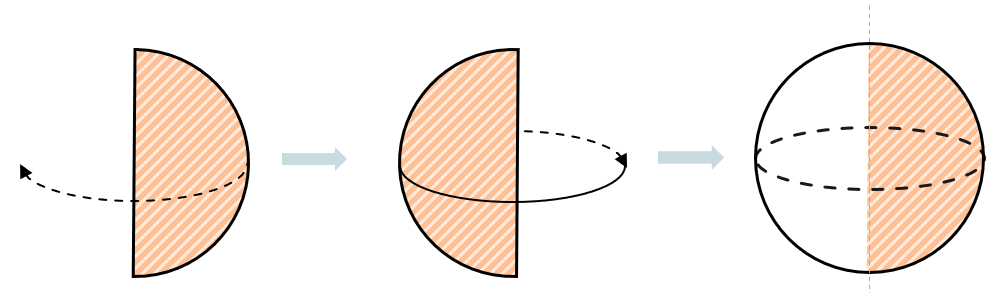
Сфера образована вращением полукруга около диаметра. Диаметр этой окружности становится осью шара:



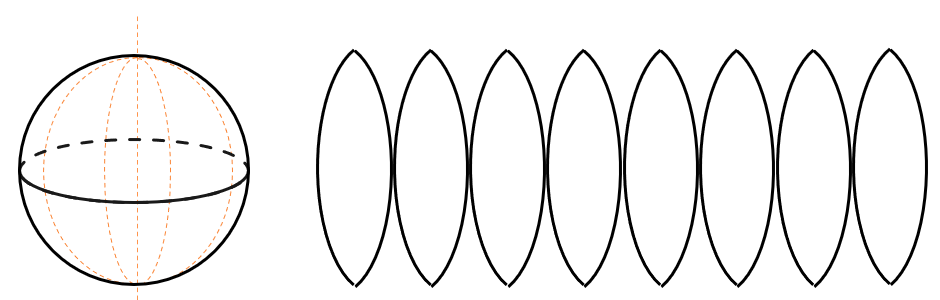
Развертка шара сложнее, чем у других геометрических тел, потому что у шара совсем нет плоских частей, например оснований. Можно представить развертку шара как перенос изображения нашей планеты с объемного глобуса на плоскую карту. Для этого используют меридианы на глобусе. Если мысленно «разрезать» глобус по каждому меридиану и развернуть его, то мы получим плоскую карту. Так и получают разверту любого шара:



2. Вычисление объемов тел вращения различными способами

Существуют различные подходы к изучению вопросов измерения геометрических величин в курсе стереометрии. Рассмотрим древний опыт. Возьмем модель полу-шара и закрепим в него два гвоздя: один в центре большого круга, другой - в вершине полу-шара. Прикрепим конец нити к гвоздику, находящемуся в вершине полу-шара и покроем нитью поверхность полу-шара, складывая её спиралью. Затем также покроем основание полу-шара – большой круг. Измерив длины использованных нитей, видим, что длина нити, затраченной на покрытии основания, т. е круга радиусом, приблизительно в 2 раза меньше длины нити, покрывающей поверхности полу-шара.

Отсюда вывод: площадь поверхности полу-шара равна 2, а площадь по­верхности шара 4. Итак, площадь сферы вычисляется по формуле

S = 4πR². 

С помощью этого метода люди узнали, что площадь поверхности шара в 4 раза больше площади его большого круга.

Опытное обоснование теоретических фактов рассматривается как средство осуществления связи геометрии с практикой.

Принципиальные трудности, возникающие при изучении объемов, имеют определенную специфику. Так как для измерения объемов сравнение с единичным кубом практически вообще невозможно, ему на смену всегда приходит измерение косвенное.

Понятие объема вводится аксиоматически. Объем - это положительная величина, численное значение которой обладает следующими свойствами:

- равные тела имеют равные объемы;

- если тело разбито на части, являющиеся простыми телами, то объем этого тела равен сумме объемов его частей;

---

- объем куба, ребро которого равно единице длины, равен единице.

Объем— это положительная величина, определенная для каждого из рассматриваемых тел, числовое значение которой имеет свойства.

Рассмотрим общий способ вычисления объемов тел вращения.

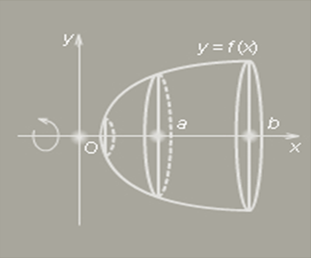
Пусть криволинейная трапеция, то есть фигура, ограниченная осью Ox, прямыми x = a, x = b и графиком непрерывной возрастающей неотрицательной функции y = f (x), вращается вокруг оси Ox, как показано на рисунке, вследствие чего образуется тело вращения. Сечение этого тела плоскостью, перпендикулярной оси Ox, есть круг или точка. На промежутке (a; b) выберем точку x. Сечение, проведенное через эту точку перпендикулярно оси Ox, есть круг площадью S (x) = πf ² (x). Объем части тела вращения, ограниченной сечениями, проведенными через точки a и x, обозначим через V (x), а объем данного тела вращения – через V.

Теорема: Объем тела вращения равен

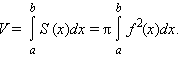Доказательство:


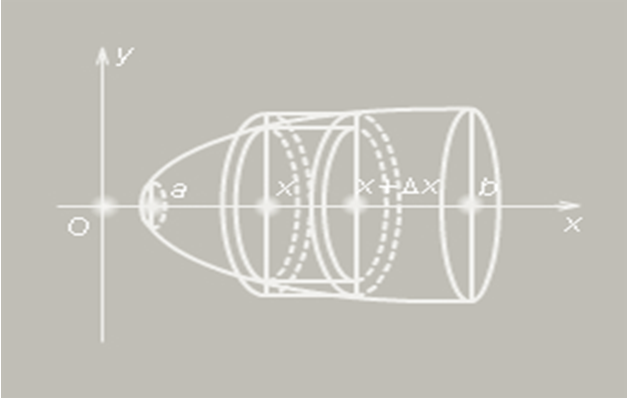
Придадим х приращение ∆х (х+∆х b). Построим два цилиндра с общей высотой ∆х. Меньший цилиндр имеет своим основанием круг, площадью S(x), а больший – круг площадью S(x+∆x). Если ∆V- прирост объёма тела вращения, то

,

откуда .

Поскольку функция f(x) непрерывна и функция следовательно



Переходя к пределу в двойном неравенстве имеем

, то есть

---

Смотрите также файлы

• Дипломная работа по теме Разработка технологического процесса сварки и изготовления котла отопления.docx

• Врачебный контроль.docx

• Основные системы управления запасами и их характеристика.docx

• Илиал Федерального государственного бюджетного образовательного учреждения высшего образования.docx

• Министерство здравоохранния донецкой народной республики.docx