ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 74
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Объем V(x) является первообразной для функции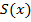
на промежутке [a;b].
Отсюда имеем
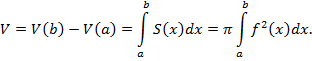
Теорема: объем шара равен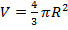
, где R-радиус шара
Доказательство:
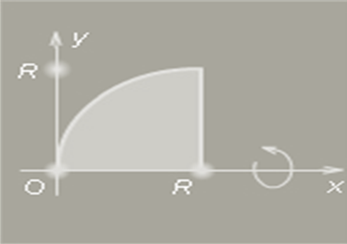
На рисунке изображена четверть круга радиуса R с центром в точке (R;0). Уравнение окружности этого круга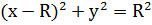
, откуда 
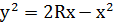. Функция 
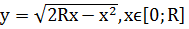непрерывная, возрастающая, неотрицательная, следовательно для нахождения объема тела вращения можно использовать предыдущую теорему. Вследствие вращения четверти круга вокруг оси Ох образуется полушар. Следовательно 
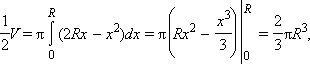откуда 
.
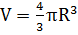Вывод формул геометрических тел на основе свойств объемов
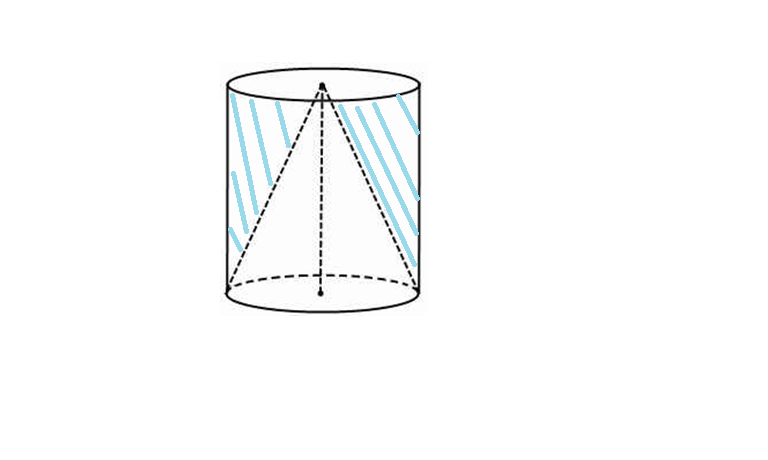
Для цилиндра и конуса.
Через систему вписанных и описанных правильных призм при условии, что
. Общую величину к которой стремятся объемы вписанных и описанных правильных призм и принимают за объем цилиндра:
Vц = SоснH
Vц=
r2H
У конуса аналогично с пирамидами: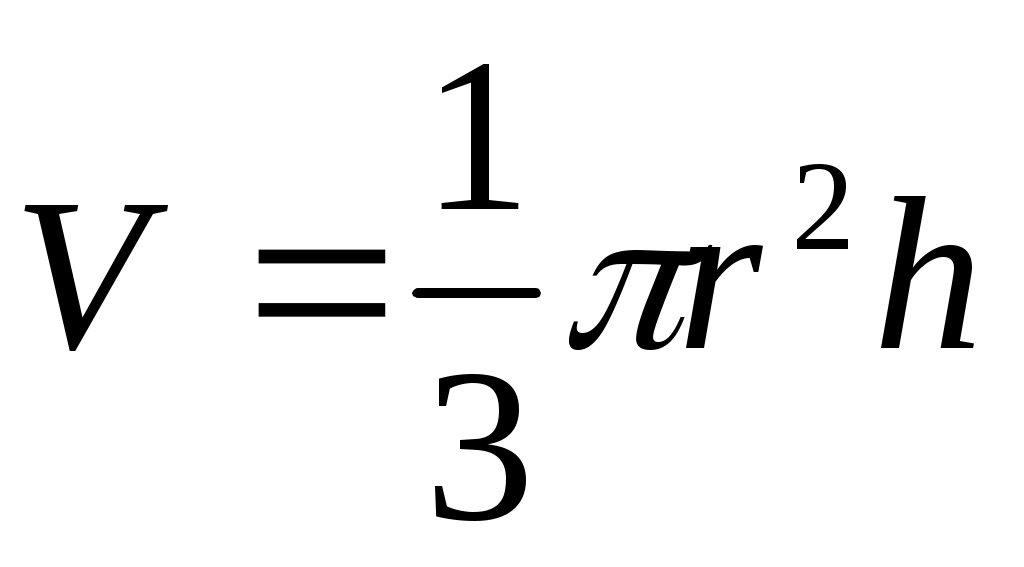
.
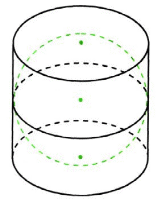
Для сферы, полушара: проводят сечения параллельные экватору и принимают их за основание цилиндра с высотой R. Получают «ступенчатое тело», состоящее из цилиндров. Число . Число к которому стремится объем цилиндров принимают за объем полушара. Следовательно, объем шара равен 2 умноженное на объем полушара, т.е.
.
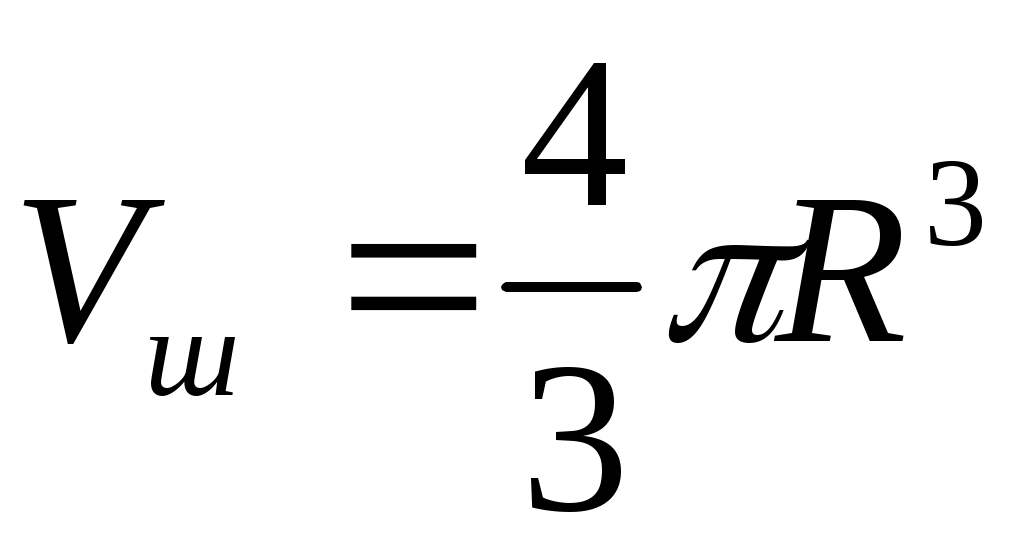3. Принцип Кавальери
Задачи об измерении объема шара и площади его поверхности были решены Архимедом в его сочинении “О шаре и цилиндре”. Вот как формулировал Архимед доказанные им теоремы: “для всякого шара цилиндр, имеющий основанием большой круг этого шара, а высотой - прямую, равную диаметру шара, и сам будет в полтора раза больше этого шара, и поверхность его тоже в полтора раза больше поверхности шара”
Итак, Архимед утверждает, что объем шара радиуса R вычисляется по формуле V=2/3(πR2•2R) т.е. V=4/3πR3, а площадь его поверхности S=2/3(2πR•2R+2π2R), т.е. S=4πR2.
Вывод формулы у Архимеда весьма сложен и занимает десятки страниц. Воспользуемся принципом, который сформулировал в ХУ11 веке итальянский математик Бонавентура Кавальери (1598-1647). Этот принцип гласит: если два тела могут быть помещены в такое положение, при котором всякая плоскость, параллельная какой-либо плоскости и пересекающая оба тела, дает в сечении с ними равновеликие фигуры, то объемы таких тел равны.
Обоснование этому принципу, как и всей теории площадей и объемов криволинейных фигур, дается в интегральном исчислении, созданным Исааком Ньютоном (1643-1727) и немецким ученым Готфридом Лейбницем (1646-1716) в конце ХУ11 века. Архимед для доказательства своих теорем предвосхитил методы интегрального исчисления на 2000 лет. Архимед очень гордился этими открытиями и по его воле на его могильной плите был изображен цилиндр с вписанным шаром, а эпитафия гласила, что их объемы относятся как 3:2.
Опираясь на принцип Кавальери, можно утверждать, что объем шара радиуса R равен оставшийся части цилиндра С с высотой 2R и радиусом основания R, из которого удалили два конуса, изображенные на рисунке
Действительно, площади заштрихованных сечений (круга и кольца), как нетрудно подсчитать, равны. Поэтому объем V шара радиуса R равен объему цилиндра С без удвоенного объема конуса с высотой R и радиусом основания также R, т.е.
V= πR2•2R – 2/3πR2•R=4/3πR2
.
Равенство установлено.
4.Практическое применение
4.1 Задачи на объёмные тела.
Задача№1
Решение:
Vцилиндра= 8∙3=24.
Значит, фигура вне конуса, но внутри цилиндра имеет объём 24-8=16
Ответ: 16
З
Дано:
В цилиндр вписан конус
Vцилиндра=36
Найти:
Vконуса
адача №2
Решение:
Задача Архимеда - объём вписанного в цилиндр конуса втрое меньше объёма цилиндра:
Vкон.=1/3
Vцил.= 1/3 ∙ 36=12
Ответ: 12
Задача №4
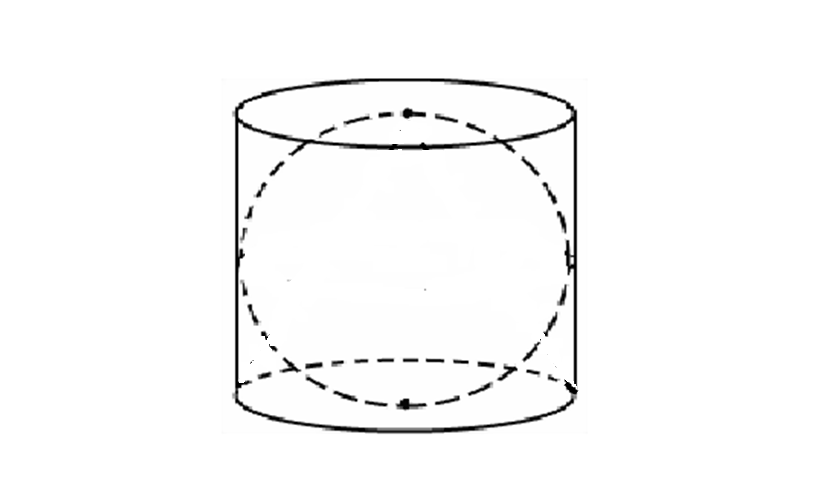
Решение:
Площадь полной поверхности цилиндра находим по формуле
Sц = 2πrh + 2πr2.
Радиус основания цилиндра (r) равен радиусу вписанного шара (R), а его высота (h) равна диаметру шара (удвоенному радиусу).
Поэтому Sц = 2πR·2R + 2πR2 = 6πR2.
Величину πR2 найдем из формулы поверхности шара Sш =4πR2. Следовательно, πR2 = Sш /4 = 111/4.
Окончательно находим Sц = 6·111/4 = 333/2 = 166,5.
Ответ: 166,5
4.2 Объёмные тела в архитектуре.
Я считаю, что данная тема проекта актуальна, потому что она, в первую очередь, расширяет интересы в области геометрии. Затем позволяет нам узнать о том, что геометрические фигуры встречаются и окружают нас в нашей повседневной жизни. Также многие архитекторы создают проекты будущих сооружений с использованием объёмных тел.
Рассмотрим объёмные тела на примере архитектурных сооружений города Волгограда.
Музей-заповедник «Сталинградская битва» г.Волгоград
Зал Воинской Славы г.Волгоград
Гипотеза: предположим, что самое комфортное жильё имеет форму шара.
Коэффициент комфортности жилья К=36ПV²/S³
K-коэффициент комфортности жилья
П-3.14
V-объём
S-площадь
Исследование жилья в форме шара.
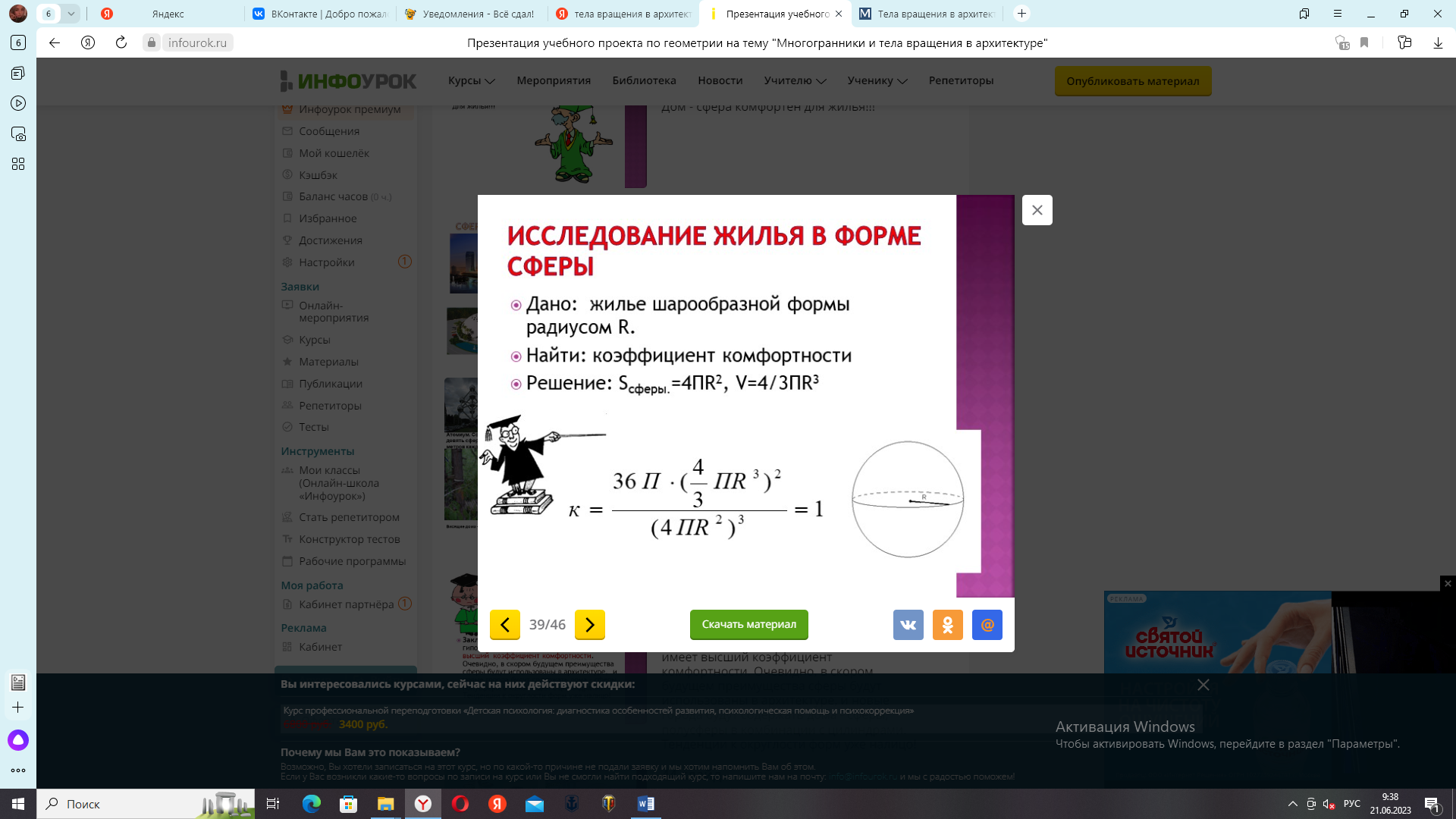
Дано: жильё шарообразной формы с радиусом R.
Найти: коэффициент комфортности
Решение: Sсферы=4ПR2, V=4/3ПR3
Вывод:
Мы получили наибольший процент комфортности жилья.
Дом-сфера комфортен для жилья!
Примеры сооружений в форме сферы.
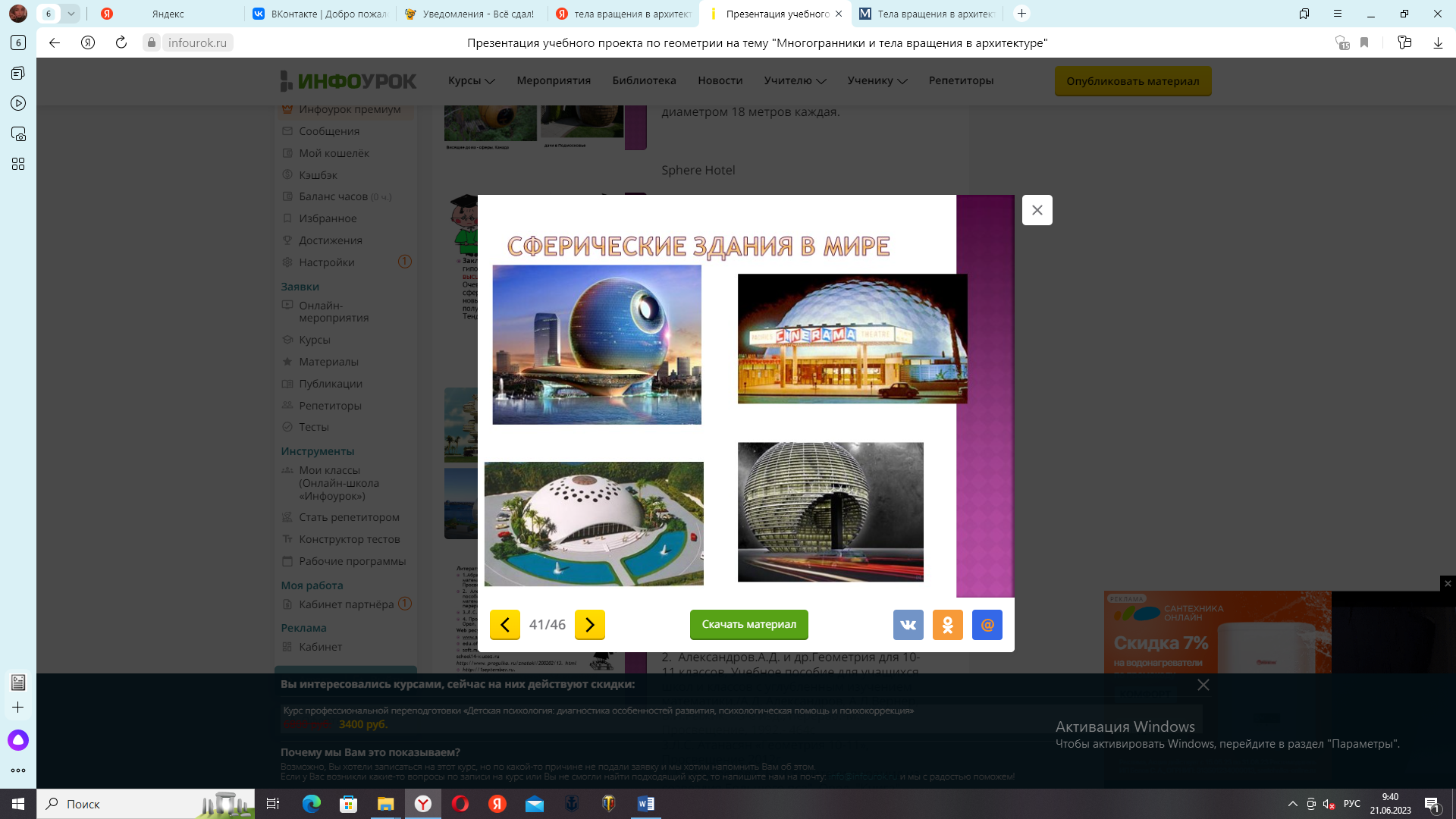
Атониум. г. Брюссель
Сооружение имеет 9 сфер с радиусом 18м. каждая.
Висящие дома-сферы. Канада.
Исследование подтвердило гипотезу: жильё в форме сферы имеет высший коэффициент комфортности. Очевидно в скором будущем преимущества сферы будут использованы в архитектуре, и новые города будут содержать дома-сферы, полусферы в комбинации с цилиндрами.
Пример города будущего.
ЗАКЛЮЧЕНИЕ
На протяжении всей истории человечества тела вращения восхищали совершенством форм и широтой областей, в которых их можно применять. Данная тема расширяет интересы в области геометрии. Познакомившись с теоретическими аспектами, считаю, что полученные знания смогу использовать в своей учебной деятельности, самостоятельно применять теоремы к определенным задачам, применять изученные теоремы в реальной ситуации.
В дальнейшем предполагаю продолжить работу над изучением данной темы. Для решения этих проблем ставлю следующие задачи:
более глубокое изучение литературы по теме «Объёмные тела. Тела вращения»,
расширить подбор задач.
СПИСОК ЛИТЕРАТУРЫ
1. Александров А.Д. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни [Текст] / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. М.: Просвещение, 2014. 255 с.
2. Атанасян, Л.С. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2 [Текст] / Л.С. Атанасян, В.Т. Базылев. М.: Просвещение, 1987. 352 с.
3. Готман, Э.Г. Стереометрические задачи и методы их решения [Текст] / Э.Г. Готман. М.: МЦНМО, 2006. 160 с.
4. Калинин, А.Ю. Геометрия. 1011 классы. Новое изд., испр. и доп. [Текст] / А.Ю. Калинин, Д.А. Терёшин. М.: МЦНМО, 2011. 640 с.
5. Оболенский, А.Ю. Лекции по аналитической геометрии: Учебно-методическое пособие [Текст] / А.Ю. Оболенский, И.А. Оболенский. Москва-Ижевск: Институт компьютерных исследований, 2004. 216 с.
6. Понарин, Я.П. Элементарная геометрия: В 2 т. Т.2: Стереометрия, преобразования пространства [Текст] / Я.П. Понарин. М.: МЦНМО, 2006. 256 с.
7. Потоскуев, Е.В. Геометрия. 11 кл.: Учеб. для общеобразоват. учреждений с углубл. и профильным изучением математики [Текст] / Е.В. Потоскуев, Л.И. Званич. М.: Дрофа, 2004. 368 с.
8. Хрестоматия по истории математики. Арифметика и алгебра. Теория чисел. Геометрия. Пособие для студентов физ.мат. фак. пед. ин-тов. [Текст] / под ред. А. П. Юшкевича. М.: Просвещение, 1976. 318 с.
9. Коксетер Г.С. Грейтцер С.Л. Новые встречи с геометрией. – М.: Наука, 1978.
10. Понарин Я.П. Элементарная геометрия. Т.1. – М.: МЦНМО, 2004.
Объем V(x) является первообразной для функции
на промежутке [a;b].Отсюда имеем
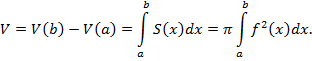
Теорема: объем шара равен
, где R-радиус шараДоказательство:
На рисунке изображена четверть круга радиуса R с центром в точке (R;0). Уравнение окружности этого круга
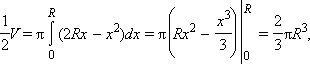, откуда . Функция непрерывная, возрастающая, неотрицательная, следовательно для нахождения объема тела вращения можно использовать предыдущую теорему. Вследствие вращения четверти круга вокруг оси Ох образуется полушар. Следовательно откуда . Вывод формул геометрических тел на основе свойств объемов
Для цилиндра и конуса.
Через систему вписанных и описанных правильных призм при условии, что
. Общую величину к которой стремятся объемы вписанных и описанных правильных призм и принимают за объем цилиндра: Vц = SоснH
Vц=
r2HУ конуса аналогично с пирамидами:
.Для сферы, полушара: проводят сечения параллельные экватору и принимают их за основание цилиндра с высотой R. Получают «ступенчатое тело», состоящее из цилиндров. Число
. Число к которому стремится объем цилиндров принимают за объем полушара. Следовательно, объем шара равен 2 умноженное на объем полушара, т.е. .3. Принцип Кавальери
Задачи об измерении объема шара и площади его поверхности были решены Архимедом в его сочинении “О шаре и цилиндре”. Вот как формулировал Архимед доказанные им теоремы: “для всякого шара цилиндр, имеющий основанием большой круг этого шара, а высотой - прямую, равную диаметру шара, и сам будет в полтора раза больше этого шара, и поверхность его тоже в полтора раза больше поверхности шара”
Итак, Архимед утверждает, что объем шара радиуса R вычисляется по формуле V=2/3(πR2•2R) т.е. V=4/3πR3, а площадь его поверхности S=2/3(2πR•2R+2π2R), т.е. S=4πR2.
Вывод формулы у Архимеда весьма сложен и занимает десятки страниц. Воспользуемся принципом, который сформулировал в ХУ11 веке итальянский математик Бонавентура Кавальери (1598-1647). Этот принцип гласит: если два тела могут быть помещены в такое положение, при котором всякая плоскость, параллельная какой-либо плоскости и пересекающая оба тела, дает в сечении с ними равновеликие фигуры, то объемы таких тел равны.
Обоснование этому принципу, как и всей теории площадей и объемов криволинейных фигур, дается в интегральном исчислении, созданным Исааком Ньютоном (1643-1727) и немецким ученым Готфридом Лейбницем (1646-1716) в конце ХУ11 века. Архимед для доказательства своих теорем предвосхитил методы интегрального исчисления на 2000 лет. Архимед очень гордился этими открытиями и по его воле на его могильной плите был изображен цилиндр с вписанным шаром, а эпитафия гласила, что их объемы относятся как 3:2.
Опираясь на принцип Кавальери, можно утверждать, что объем шара радиуса R равен оставшийся части цилиндра С с высотой 2R и радиусом основания R, из которого удалили два конуса, изображенные на рисунке
Действительно, площади заштрихованных сечений (круга и кольца), как нетрудно подсчитать, равны. Поэтому объем V шара радиуса R равен объему цилиндра С без удвоенного объема конуса с высотой R и радиусом основания также R, т.е.
V= πR2•2R – 2/3πR2•R=4/3πR2
.
Равенство установлено.
4.Практическое применение
4.1 Задачи на объёмные тела.
| Дано: Конус вписан в цилиндр Vк=8 Найти: Vфигуры между цилиндром и конусом |
Решение:
Vцилиндра= 8∙3=24.
Значит, фигура вне конуса, но внутри цилиндра имеет объём 24-8=16
Ответ: 16
З
Дано:
В цилиндр вписан конус
Vцилиндра=36
Найти:
Vконуса
адача №2
Решение:
Задача Архимеда - объём вписанного в цилиндр конуса втрое меньше объёма цилиндра:
Vкон.=1/3
Vцил.= 1/3 ∙ 36=12
Ответ: 12
| Дано: Шар вписан в цилиндр Sшара=111 Найти: Sцилиндра |
Задача №4
Решение:
Площадь полной поверхности цилиндра находим по формуле
Sц = 2πrh + 2πr2.
Радиус основания цилиндра (r) равен радиусу вписанного шара (R), а его высота (h) равна диаметру шара (удвоенному радиусу).
Поэтому Sц = 2πR·2R + 2πR2 = 6πR2.
Величину πR2 найдем из формулы поверхности шара Sш =4πR2. Следовательно, πR2 = Sш /4 = 111/4.
Окончательно находим Sц = 6·111/4 = 333/2 = 166,5.
Ответ: 166,5
4.2 Объёмные тела в архитектуре.
Я считаю, что данная тема проекта актуальна, потому что она, в первую очередь, расширяет интересы в области геометрии. Затем позволяет нам узнать о том, что геометрические фигуры встречаются и окружают нас в нашей повседневной жизни. Также многие архитекторы создают проекты будущих сооружений с использованием объёмных тел.
Рассмотрим объёмные тела на примере архитектурных сооружений города Волгограда.
Музей-заповедник «Сталинградская битва» г.Волгоград
Зал Воинской Славы г.Волгоград
Гипотеза: предположим, что самое комфортное жильё имеет форму шара.
Коэффициент комфортности жилья К=36ПV²/S³
K-коэффициент комфортности жилья
П-3.14
V-объём
S-площадь
Исследование жилья в форме шара.
Дано: жильё шарообразной формы с радиусом R.
Найти: коэффициент комфортности
Решение: Sсферы=4ПR2, V=4/3ПR3
Вывод:
Мы получили наибольший процент комфортности жилья.
Дом-сфера комфортен для жилья!
Примеры сооружений в форме сферы.
Атониум. г. Брюссель
Сооружение имеет 9 сфер с радиусом 18м. каждая.
Висящие дома-сферы. Канада.
Исследование подтвердило гипотезу: жильё в форме сферы имеет высший коэффициент комфортности. Очевидно в скором будущем преимущества сферы будут использованы в архитектуре, и новые города будут содержать дома-сферы, полусферы в комбинации с цилиндрами.
Пример города будущего.
ЗАКЛЮЧЕНИЕ
На протяжении всей истории человечества тела вращения восхищали совершенством форм и широтой областей, в которых их можно применять. Данная тема расширяет интересы в области геометрии. Познакомившись с теоретическими аспектами, считаю, что полученные знания смогу использовать в своей учебной деятельности, самостоятельно применять теоремы к определенным задачам, применять изученные теоремы в реальной ситуации.
В дальнейшем предполагаю продолжить работу над изучением данной темы. Для решения этих проблем ставлю следующие задачи:
более глубокое изучение литературы по теме «Объёмные тела. Тела вращения»,
расширить подбор задач.
СПИСОК ЛИТЕРАТУРЫ
1. Александров А.Д. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни [Текст] / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. М.: Просвещение, 2014. 255 с.
2. Атанасян, Л.С. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2 [Текст] / Л.С. Атанасян, В.Т. Базылев. М.: Просвещение, 1987. 352 с.
3. Готман, Э.Г. Стереометрические задачи и методы их решения [Текст] / Э.Г. Готман. М.: МЦНМО, 2006. 160 с.
4. Калинин, А.Ю. Геометрия. 1011 классы. Новое изд., испр. и доп. [Текст] / А.Ю. Калинин, Д.А. Терёшин. М.: МЦНМО, 2011. 640 с.
5. Оболенский, А.Ю. Лекции по аналитической геометрии: Учебно-методическое пособие [Текст] / А.Ю. Оболенский, И.А. Оболенский. Москва-Ижевск: Институт компьютерных исследований, 2004. 216 с.
6. Понарин, Я.П. Элементарная геометрия: В 2 т. Т.2: Стереометрия, преобразования пространства [Текст] / Я.П. Понарин. М.: МЦНМО, 2006. 256 с.
7. Потоскуев, Е.В. Геометрия. 11 кл.: Учеб. для общеобразоват. учреждений с углубл. и профильным изучением математики [Текст] / Е.В. Потоскуев, Л.И. Званич. М.: Дрофа, 2004. 368 с.
8. Хрестоматия по истории математики. Арифметика и алгебра. Теория чисел. Геометрия. Пособие для студентов физ.мат. фак. пед. ин-тов. [Текст] / под ред. А. П. Юшкевича. М.: Просвещение, 1976. 318 с.
9. Коксетер Г.С. Грейтцер С.Л. Новые встречи с геометрией. – М.: Наука, 1978.
10. Понарин Я.П. Элементарная геометрия. Т.1. – М.: МЦНМО, 2004.