Задача
Для цепи, приведенной на рис. 1.1 с параметрами: R₁ = 1 Ом;R₂ = 1 Ом;R₃ = 1 Ом;R₄ = 6 Ом;R₅ = 6 Ом;R₆ = 4 Ом;E₁ = 8 В; E₂ = 10 В; Е₃ = 6 В определить токи во всех ветвях методом непосредственного применения законов Кирхгофа.

Ответ представить в виде графического файла электрической схемы, с принятыми направлениями токов во всех ветвях и результатами вычисления токов во всех ветвях.



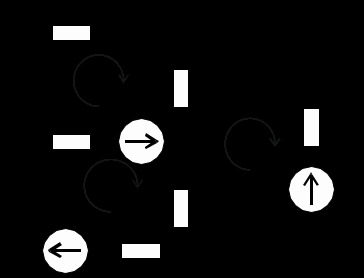
Рисунок 1.1  Расчетная схема
Решение

При составлении независимых уравнений баланса токов возьмем за положительное направление тока направление тока ветви к узлу, и отрицательное значение тока, если ток ветви направлен от узла.

Для составления независимых уравнений баланса напряжений выбираем независимые (главные) контуры, чтобы каждый контур отличался от остальных хотя бы одной ветвью  главной ветвью. Напряжения ветви берется со знаком плюс, если направление обхода контура совпадает с направлением напряжения, если не совпадает, то со знаком минус.

Количество уравнений, составленных по первому закону Кирхгофа, бу­дет определяется по формуле m = q  1, где q  количество узлов.

m = q – 1 = 4 – 1 = 3.

для узла a  I₁ + I₂ + I₄ = 0;

для узла b I₁  I₅  I₆ = 0;

для узла c I₃  I₄ + I₅ = 0.

По второму закону Кирхгофа:

для первого контура I (R₁_E₁_R₆_R₂_E₂) U₁ + U₂ + U₆ = E₁ + E₂;

для второго контура II (R₄_R₅_E₁_R₁)  U₁  U₄  U₅ =  E₁;

для второго контура III (R₃_E₃_R₆_R₅)  U₃ + U₅  U₆ =  E₃.

Количество компонентных уравнений равно числу ветвей, а для данной схемы их число равно 6:

для первой ветви U₁ = I₁R₁;

для второй ветви U₂ = I₂R₂;

для третьей ветви U

---

₃ = I₃R₃;

для четвертой ветви U₄ = I₄R₄;

для пятой ветви U₅ = I₅R₅;

для шестой ветви U₆ = I₆R₆.

Для уменьшения количества неизвестных, в связи с необходимостью определения токов, подставим в уравнения по второму закону Кирхгофа компонентные уравнения.

Система линейно-независимых уравнений баланса токов будет иметь следующий вид:

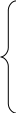 I₁ + I₂ + I₄ = 0;

I₁  I₅  I₆ = 0;

I₃  I₄ + I₅ = 0;

I₁R₁ + I₂R₂ + I₆R₆ = E₁ + E₂;

 I₁R₁  I₄R₄  I₅R₅ =  E₁;

 I₃R₃ + I₅R₅  I₆R₆ =  E₃.

Полученную систему уравнений решим с помощью программы MathCad (рис. 1.2).



Рисунок 1.2  Решение системы уравнений в программеMathcad 15
Таким образом, получено

I₁ = 3,488 А; I₂ = 3,46133 А; I₃ =  0,69867 А;I₂ = 0,02667 А; I₅ = 0,72533 А; I₆ = 2,76267 А.

Знак минус у третьего тока означает, что в реальной схеме ток протекает в сторону, противоположную выбранному нами изначально на схеме.

Электрическая схема, со значениями протекающих токов в ветвях приведена на рис. 1.3.



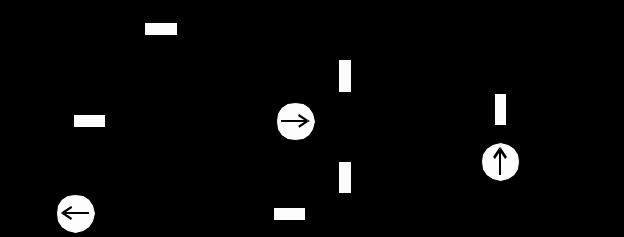
Рисунок 1.3  Электрическая схема, со значениями протекающих
токов в ветвях
Проверку рассчитанных токов выполним путем моделирования и расчета токов схемы в программе MicroCap 9. Сформированная схема приведена на рисунке 1.4.



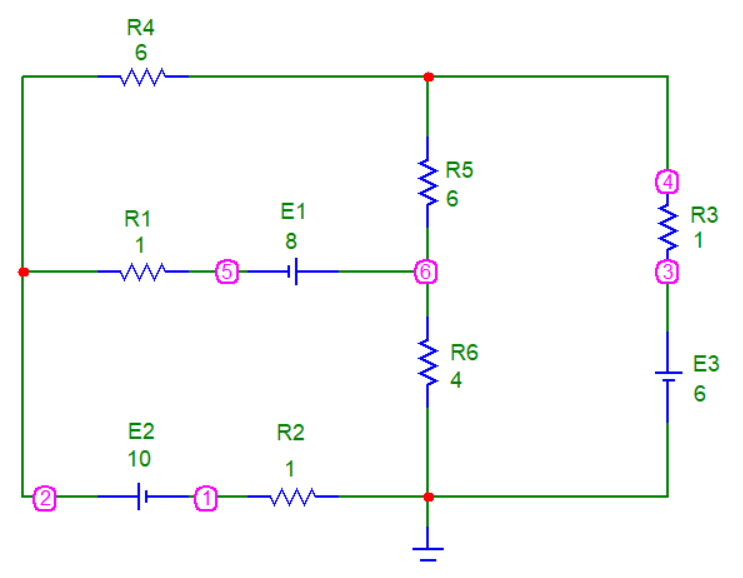
Рисунок 1.4  Схема, сформированная в программе MicroCap 9
После запуска схемы на расчет по переменному току, с выполнением всех настроек по умолчанию без изменений, выходу из режима расчета схемы по переменному току с включением отображения токов в схеме получим значения токов в ветвях схемы (рис. 1.5, значения синим цветом в синих прямоугольных областях).

---

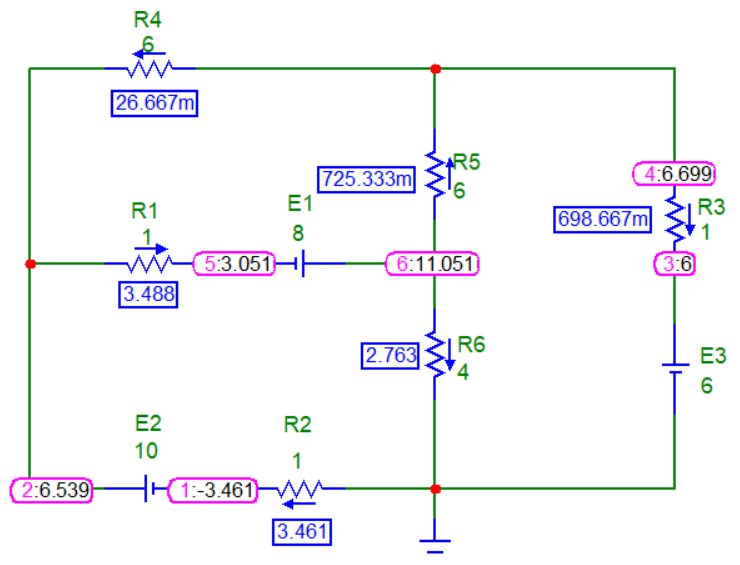
Рисунок 1.5  Результаты расчетов в программе MicroCap 9
Токи, найденные методом законов Кирхгофа с точностью до миллиампера, полностью совпадают с токами, найденными при моделировании схемы в программе Micro Cap 9 для этой же цепи, что говорит о правильности решения.

---

Смотрите также файлы

• Предмет, метод, система, источники и субъекты административного права. Административное право.docx

• Оссийской федерации филиал.pdf

• 2. На график движения наносятся все поезда.docx

• Изучите систему кадровой безопасности в организации, на базе.docx

• Громов В. Г. Вопросы безопасности в исправительных учреждениях Уголовноисполнительное право. 2022. 4. С. 459464.docx