Исходные данные

Профиль №1

Полоса 200x5

A1 = 10см2

JX1 = 0.2083см4

JY1 = 333.3см4

 

Профиль №2

Уголок 90x90x6

A2 = 10.61см2

JX2 = JX(90°) = 82.1см4

JY2 = JY(90°) = 82.1см4

JX2Y2 = JXY(90°) = 48.1см4

 

Профиль №3

Уголок 90x90x6

A3 = 10.61см2

JX3 = 82.1см4

JY3 = 82.1см4

JX3Y3 = -48.1см4

 

Профиль №4

Двутавр №20

A4 = 26.8см2

JX4 = 1840см4

JY4 = 115см4

 

Профиль №5

Двутавр №20

A5 = 26.8см2

JX5 = 1840см4

JY5 = 115см4

 

Профиль №6

Полоса 200x5

A6 = 10см2

JX6 = 0.2083см4

JY6 = 333.3см4

 
Расчёт

1. Определение площади всего сечения

A = ∑A_i = 10 + 10.61 + 10.61 + 26.8 + 26.8 + 10 = 94.82см²,

где, A_i - площадь i-го профиля.

2. Определение положения центра тяжести сечения

x_C = ∑(A_i·x_i)/A = (10 · 10 + 10.61 · 17.57 + 10.61 · 2.43 + 26.8 · 5 + 26.8 · 15 + 10 · 10) / 94.82 = 10см,

y_C = ∑(A_i·y_i)/A = (10 · 20.5 + 10.61 · 23.18 + 10.61 · 23.18 + 26.8 · 10.25 + 26.8 · 10.25 + 10 · 0.25) / 94.82 = 13.17см,

---

где, x_i, y_i - координаты центра тяжести i-го профиля в системе координат XY.

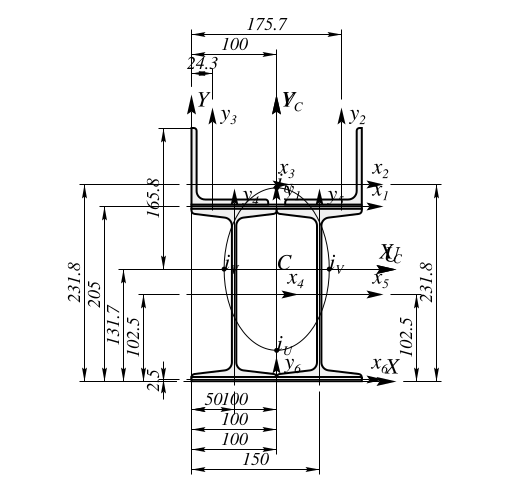Рис. 1. Эскиз сечения

3. Определение моментов инерции всего сечения относительно центральной системы координат X_CY_C.

J_XC = ∑J⁽ⁱ⁾_XC,

J_YC = ∑J⁽ⁱ⁾_YC,

J_XCY_C = ∑J⁽ⁱ⁾_XCYC,

где, J_XC, J_YC, J_XCY_C - осевые моменты и центробежный момент инерции сечения соответственно, J⁽ⁱ⁾_XC,J⁽ⁱ⁾_YC,J⁽ⁱ⁾_XCYC - осевые моменты и центробежный момент инерции i-го профиля, которые определяются по следующим формулам:

J⁽ⁱ⁾_XC = J_xi + a_i·A_i,

J⁽ⁱ⁾_YC = J_yi + b_i·A_i,

J⁽ⁱ⁾_XCYC = J_xiy_i + a_i·b_i·A_i,

где, a_i = y_i - y_C, b_i = x_i - x_C - смещения центра тяжести i-го профиля по осям Y_C и X_C соответственно.

Определим смещения центра тяжести каждого профиля.

Для профиля №1 "Полоса 200x5":

a₁ = 20.5 - 13.17 = 7.33см,

b₁ = 10 - 10 = -1.776·10^-15см.

Для профиля №2 "Уголок 90x90x6":

a₂ = 23.18 - 13.17 = 10.01см,

b₂ = 17.57 - 10 = 7.57см.

Для профиля №3 "Уголок 90x90x6":

a₃ = 23.18 - 13.17 = 10.01см,

b₃ = 2.43 - 10 = -7.57см.

Для профиля №4 "Двутавр №20":

a₄ = 10.25 - 13.17 = -2.92см,

b₄ = 5 - 10 = -5см.

Для профиля №5 "Двутавр №20":

a₅ = 10.25 - 13.17 = -2.92см,

b₅ = 15 - 10 = 5см.

Для профиля №6 "Полоса 200x5":

a₆ = 0.25 - 13.17 = -12.92см,

b₆ = 10 - 10 = -1.776·10^-15см.

Далее определим осевые моменты и центробежный момент инерции каждого профиля.

Для профиля №1 "Полоса 200x5":

J⁽¹⁾_XC = 0.2083 + 7.33² · 10 = 537.5см⁴,

J⁽¹⁾_YC = 333.3 + (-1.776·10^-15)² · 10 = 333.3см⁴,

J⁽¹⁾_XCYC = 0 + 7.33 · (-1.776·10^-15) · 10 = -1.302·10^-13см⁴.

Для профиля №2 "Уголок 90x90x6":

J⁽²⁾_XC = 82.1 + 10.01² · 10.61 = 1145см⁴,

J⁽²⁾_YC = 82.1 + 7.57² · 10.61 = 690.1см⁴,

J⁽²⁾_XCYC = 48.1 + 10.01 · 7.57 · 10.61 = 852.1см⁴.

Для профиля №3 "Уголок 90x90x6":

J⁽³⁾_XC = 82.1 + 10.01² · 10.61 = 1145см⁴,

J⁽³⁾_YC = 82.1 + (-7.57)² · 10.61 = 690.1см⁴,

J⁽³⁾_XCYC = -48.1 + 10.01 · (-7.57) · 10.61 = -852.1см

---

⁴.

Для профиля №4 "Двутавр №20":

J⁽⁴⁾_XC = 1840 + (-2.92)² · 26.8 = 2069см⁴,

J⁽⁴⁾_YC = 115 + (-5)² · 26.8 = 785см⁴,

J⁽⁴⁾_XCYC = 0 + (-2.92) · (-5) · 26.8 = 391.3см⁴.

Для профиля №5 "Двутавр №20":

J⁽⁵⁾_XC = 1840 + (-2.92)² · 26.8 = 2069см⁴,

J⁽⁵⁾_YC = 115 + 5² · 26.8 = 785см⁴,

J⁽⁵⁾_XCYC = 0 + (-2.92) · 5 · 26.8 = -391.3см⁴.

Для профиля №6 "Полоса 200x5":

J⁽⁶⁾_XC = 0.2083 + (-12.92)² · 10 = 1669см⁴,

J⁽⁶⁾_YC = 333.3 + (-1.776·10^-15)² · 10 = 333.3см⁴,

J⁽⁶⁾_XCYC = 0 + (-12.92) · (-1.776·10^-15) · 10 = 2.295·10^-13см⁴.

Моменты инерции всего сечения относительно центральной системы координат X_CY_C будут равны:

J_XC = 537.5 + 1145 + 1145 + 2069 + 2069 + 1669 = 8634см⁴,

J_YC = 333.3 + 690.1 + 690.1 + 785 + 785 + 333.3 = 3617см⁴,

J_XCY_C = 1.302·10^-13 + 852.1 - 852.1 + 391.3 - 391.3 + 2.295·10^-13 = 5.898·10^-14см⁴.

4. Определение угла поворота главной центральной системы координат UV.

Тангенс угла поворота системы координат UV относительно системы координат X_CY_C определится по следующей формуле

tg(2α) = -2J_XCY_C / (J_XC - J_YC) = -2·5.898·10^-14 / (8634 - 3617) = -2.3508·10^-17.

Откуда угол поворота будет равен

α = 0°.

5. Определение главных центральных моментов сечения

J_max,min = (J_XC + J_YC) / 2 ± 0.5·[(J_XC - J_YC)² + 4·J_XCY_C²]^0.5 = (8634 + 3617) / 2 ± 0.5·[(8634 - 3617)² + 4·(5.898·10^-14)²]^0.5 = 6126 ± 2509.

Следовательно,

J_min = J_V = 3617см⁴; J_max = J_U = 8634см⁴.

6. Определение главных центральных моментов сопротивления сечения

Из определения моментов сопротивления сечения

W_U = J_U / |V_max|; W_V = J_V / |U_max|.

Из эскиза сечения найдем

|U_max| = 10см; |V_max| = 16.58см.

Главные центральные моменты сопротивления сечения будут равны

W_U = 8634 / 16.58 = 520.8см³; W_V = 3617 / 10 = 361.7см³.

7. Определение главных радиусов инерции

---

i_V = i_min = (J_V / A)^0.5 = (3617 / 94.82)^0.5 = 6.176см; i_U = i_max = (J_U / A)^0.5 = (8634 / 94.82)^0.5 = 9.543см.

Задача решена.

---

Смотрите также файлы

• Методические указания по выполнению рейтинговой работы по дисциплине Интеллектуальные информационные системы.docx

• Фыыччавпвапвап тайное внедрение своего сотрудника в окружение оппонента за 36 месяцев до предполагаемого начала переговоров 26. Ошибкой при разрешении конфликтов будет.docx

• штерек ауылы орта мектебі Жиынты баалау жргізу орытындылары бойынша талдау мліметтер іv тосан.docx

• Старость не радость, маразм не оргазм Ольга Бондаренко Автономова.docx

• Нарастание кризисных явлений в Римской империи, включая усиливающееся расслоение общества и нарастание социального и иных видов отчуждения.docx