1 вопрос

Метод круглоцилиндрических поверхностей скольжения широко применяется на практике, так как дает некоторый запас устойчи­вости и основывается на опытных данных о форме поверхностей скольжения при оползнях вращения, которые на основании мно­гочисленных замеров в на­туре (например, Шведской геотехнической комиссии, управления канала Моск­ва — Волга и др.) прини­мают за круглоцилиндриче­ские, при этом самое невы­годное их положение оп­ределяется расчетом. При­нятие определенной формы поверхностей скольжения и ряда других допущений (о чем будет сказано ниже) делает этот метод прибли­женным.

Допустим, что центр круглоцилиндрической по­верхности скольжения X оползающей призмы нахоДится в точкеО

Уравнением рав­новесия будет 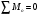Для составления уравнения моментов от­носительно точки вращения О разбивают призму скольжения АВС вертикальными сечениями на ряд отсеков и принимают вес каждо­го отсека условно приложенным в точке пересечения веса отсека P_iс соответствующим отрезком дуги скольжения, а силами взаимодей­ствия по вертикальным плоскостям отсека (считая, что давления от соседних отсеков равны по величине, а по направлению противопо­ложны) пренебрегают. Раскладывая далее силы веса Р/ на направле­ние радиуса вращения и ему перпендикулярное, составляют уравне­ние равновесия, приравнивая ну­лю момент всех сил относитель­но точки вращения: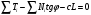



Здесь L—длина дуги сколь­жения АС; 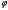, с — угол внут­реннего трения и сцепление грунта; T_iи N_i— составляю­щие давления от веса отсеков, определяемые графически или вы­числяемые по замерам углов а,:

T_t= Pi sin a_i; Ni — Picosa_i.

3aкоэффициент устойчивости откоса принимают отношение мо­мента сил удерживающих к мо­менту сил сдвигающих, т. е.



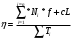
Однако решение поставлен­ной задачи определением коэф­фициента устойчивости для про­извольно выбранной дуги по­верхности скольжения не закан­чивается, так как необходимо из всех возможных дуг поверх­ностей скольжения выбрать наи­более опасную. Последнее выполняется путем попыток, задаваясь раз­личными положениями точек вращения О;

---

Для ряда намеченных центров дуг поверхностей скольжения (О,;О.,; О_л — рис. IV. 18, б) определяют необходимое но условию устойчивости сцепление, соответствующее предельному равновесию заданного откоса, по выражению, вытекающему из соотношения (у₂), а именно:



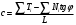
Далее, из всех возможных центров скольжения выбирают тот, для которого требуется максимальная величина сил сцепления. Этот центр принимают за наиболее опасный и для него вычисляют коэффициент устойчивости.

Вопрос 2

Оценка природного состояния грунтов.

Поскольку свойства грунтов в значительной степени предопределяются размерами и минералогическим составом слагающих их твердых частиц, последние принято классифицировать по размерам,мм: галечный (>20), гравелистый (20-2), песчаные (2-0,05), пылеватые (0,05-0,005), глинистые (<0,005).

В некоторой степени учитывается и содержание глинистых минералов. Частицы крупнее 0,05 мм обычно имеют остроугольную или округлую форму, а более мелкие глинистые ‐ пластичную, иногда игольчатую. Песчаные частицы подразделяются на крупные, средние и мелкие.

Разделение частиц грунтов по категориям обусловливается тем, что грунты, состоящие из частиц одной категории, обладают специфическими свойствами.

Песчаные частицы слагают различные по крупности пески, которые обладают водопроницаемостью, не пластичны, имеют сравнительно жесткий, малосжимаемый при действии статической нагрузки скелет

В зависимости от плотности сложения пески способны существенно уплотняться при динамических воздействиях Они характеризуются небольшой высотой капиллярного поднятия (до 0,5 м) и в сухом состоянии являются сыпучими телами.

Грунт, состоящий только из глинистых частиц, практически водонепроницаем, во влажном состоянии характеризуется высокой пластичностью, может обладать большой сжимаемостью при действии статической нагрузки, при динамических воздействиях не уплотняется, но может снижать прочность. После прекращения динамических воздействий прочность грунта постепенно частично или полностью восстанавливается, т. е. он обладает специфическими тиксотропными свойствами. Такой грунт при изменении содержания в нем воды меняет объем, набухает при увлажнении и получает усадку при высыхании.

---

По гран-составувыд-т 5 типов песчаных грунтов:

1. в грунте сод-ся частиц >2 мм – более 25% - песок гравелистый.

2. ч-ц >0,5 мм более 50% - песок крупный

3. ч-ц >0,25 мм более 50% - песок средний

4. ч-ц >0,1 мм 75% и более – песок мелкий

5. ч-ц >0,1 мм менее 75% - песок пылеватый.

По однородности мех состава: Umax=d50(d95/d5).

1) Umax<4 – однородный грунт. 2) 4
3) 2040 – повыш неоднородности

По степени влажности Sr=w*(ρs/ρw):

1) 0
Глинистые груты

Влажн при кот-й грунт переходит из тв-госост в пласт назвл-ю на границе пластичности (wp). Влажн при переходе из плсост в текучее – назвлажн на границе текучести (wl)

Число пластичности Ip=wl-wp

1) 1
2) 7
3) Ip>17 – глина.

Показатель текучести (консистенции) Il=(w-wp)/Ip.

Супеси

1) Твердые I_L<0

2) Пластичные 0L<1

3) текучие I_L>1

Суглинки и глины:

1) Твердые I_L<0

2) Полутвердые 0< I_L<0,25

3) Тугопластичные 0,25< I_L ≤0,5

4) Мягкопластичные 0,5< I_L<0,75

5) Текучепластичные 0,75< I_L<1,0

6) Текучие I_L>1.

Напряжения от собственного веса грунта

Фактическое напряженное состояние грунтов основания при современных методах изысканий точно определить не представляется возможным. В большинстве случаев ограничиваются нахождением вертикального напряжения от действия веса вышележащих грунтов. Вертикальные напряжения от собственного веса грунта называют бытовыми давлениями, а график их изменения по глубине – эпюрой бытовых давлений. Напряжения от собственного веса грунта определяются на основании следующих упрощающих гипотез: 1) напряженным состоянием грунта при действии его собственного веса является осесимметричное компрессионное сжатие; 2) вертикальные напряжения в грунте определяются суммированием напряжений от веса элементарных слоев грунта; 3) грунт, находящийся ниже уровня грунтовых вод, испытывает взвешивающее действие воды; 4) слой грунта, находящийся ниже водоносного слоя, называется водоупороми испытывает на своей поверхности гидростатическое давление водяного столба.

Определяем напряжение от собственного веса грунта (природного или бытового) по Формуле 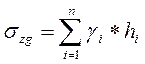  где n– число слоев грунта в пределах глубины z;

γi– удельный вес грунта i-го слоя, кН/м3;

hi– толщина или мощность этого слоя, м.

Измеряется в МПА

Удельный вес водопроницаемых грунтов, залегающих ниже уровня грунтовых вод,

принимается с учетом взвешивающего действия воды согласно выражению

γsb=(γs –γw)/(1+e),

где γw– удельный вес воды, γw= 10 кН/м3;

γs– удельный вес частиц грунта;

е– коэффициент пористости.

Формула используется для вычисления бытовых давлений на границах геологических

слоев, на линии уровня грунтовых вод и на границе водоупора. В остальных сечениях бытовые давления могут быть определены по линейной интерполяции. На рис. 4.11 представлены характерные эпюры бытовых давлений в грунтовом массиве. На границах геологических слоев угол наклона эпюры, как правило, изменяется в связи с изменением величины удельного веса грунта. На линии уровня грунтовых вод (WL)имеет место самый заметный перегиб эпюры, вызванный уменьшением удельного веса грунта во взвешенном состоянии. На границе водоупора эпюра имеет скачок на величину гидростатического давления от веса столба воды над водоупором.

3 Вопрос

Метод послойного суммирования

Расчет осадки слоистых оснований выполняется методом послойного суммирования, в основу которого положена выше разобранная задача (основная задача). Сущность метода заключается в определении осадок элементарных слоев основания в пределах сжимаемой толщи от дополнительных вертикальных напряжений σ_ZP, возникающих от нагрузок, передаваемых сооружениям.

Так как в основу этого метода положена расчетная модель основания в виде линейно-деформируемой сплошной среды, то необходимо ограничить среднее давление на основание таким пределом, при котором области возникающих пластических деформаций лишь незначительно нарушают линейную деформируемость основания, т.е. требуется удовлетворить условие

         

Для определения глубины сжимаемой толщи Н_с вычисляют напряжения от собственного веса σ_Zqи дополнительные от внешней нагрузки σ_ZP.
Нижняя граница сжимаемой толщи ВС основания принимается на глубине z = Н_с от подошвы фундамента, где выполняется условие

                  

т.е. дополнительные напряжения составляют 20% от собственного веса грунта.

При наличии нижеуказанной глубины грунтов с модулем деформации Е≤5 МПа должно соблюдаться условие

                    

Для оснований гидротехнических сооружений по СНиП 2.02.02—85 «Основания гидротехнических сооружений» нижняя граница активной зоны находится из условия

                       

Расчет осадки удобно вести с использованием графических построений в следующей последовательности

строят геологический разрез строительной площадки на месте рассчитываемого фундамента;

наносятся размеры фундамента;

строятся эпюры напряжений от собственного веса грунта σ_Zg и дополнительного σ_ZP от внешней нагрузки;

определяется сжимаемая толща Н_с;

разбивается Н_с на слои толщиной h_i≤0,4b;

определяется осадка элементарного слоя грунта по формуле

                                                                                                 

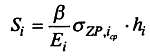
Тогда полную осадку можно найти простым суммированием осадок всех элементарных слоев в пределах сжимаемой толщи из выражения

               

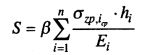
где β— безразмерный коэффициент, зависящий от коэффициента относительных поперечных деформаций, принимаемый равным 0,8; h_i— высота i-го слоя; E_i — модуль деформации i-го слоя грунта;

 — среднее напряжение i-го элементарного слоя.

Метод послойного суммирования позволяет определять осадку не только центральной точки подошвы фундамента. С его помощью можно вычислить осадку любой точки в пределах или вне пределов фундамента. Для этого пользуются методом угловых точек и строится эпюра напряжений вертикальной, проходящей через точку, для которой требуется расчет осадки.



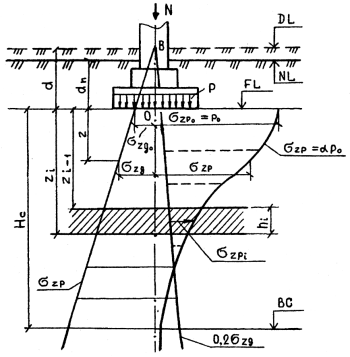
Рис. 7.11. Расчетная схема для определения осадки методом послойного суммирования: DL — отметка планировки; NL — отметка поверхности природного рельефа; FL — отметка подошвы фундамента; ВС — нижняя граница сжимаемой толщи; Нс — сжимаемая толща

Таким образом, метод послойного суммирования в основном используется при расчете небольших по размерам фундаментов зданий и сооружений и при отсутствии в основании пластов очень плотных малосжимаемых грунтов.

21. Распределение напряжений в случаеплоскойзадачи

По мере увеличенияотношениядлиныплощадизагруженияl к ширине задача по определению напряжений все с большимоснованиемможетрассматриватьсякакплоскаяОпределяют три составляющие: нормальноенапряжение 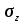, 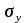и касательныенапряжения .

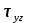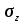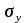
Если в изотропномтелевовсех точках сечения, перпендикулярного продольной оси нагрузки, определить , 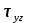. И соединить точки с одинаковымизначениямикаждойизэтих величин линиям и равных напряжений , то полуяимсвоеобразныеграфики. Последниепоказывают, чтонормальныенапряжения 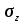распространяются на значительнуюглубину , а нормальныенапряжения 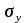и касательныенапяржения 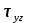- преимущественно в пределахполутора-двухширинполосызагружения.
22. Определение прочностных характеристик лабораторным и полевым методом

Характеристики прочности φ и с определяют в лабораторных и полевых условиях.

Определение прочностных характеристик в лабораторных условиях

В 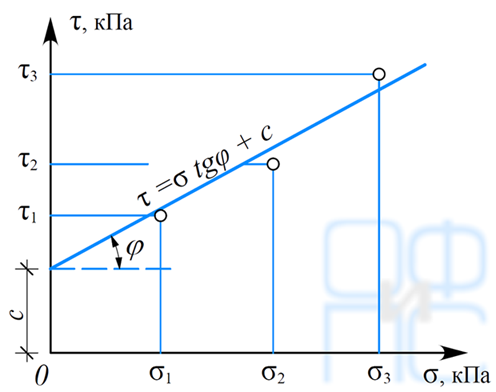практике исследований грунтов применяют метод среза грунта по фиксированной плоскости в приборах одноплоскостного среза. Для получения φ и с необходимо провести срез не менее трех образцов грунта при различных значениях вертикальной нагрузки. По полученным в опытах значениям сопротивления срезу τ строят график линейной зависимости τ = f(σ) и находят угол внутреннего трения φ и удельное сцепление с (рис. 1.5).
Рис. 1.5. Зависимость сопротивления срезу грунта τ от нормального напряжения σ

Различают две основные схемы опыта: медленный срез предварительно уплотненного до полной консолидации образца грунта (консолидировано-дренированное испытание) и быстрый срез без предварительного уплотнения (неконсолидировано-недренированное испытание).

Значения φ и с, полученные по методике медленного консолидированного среза, используются для определения расчетного сопротивления грунта, а также для оценки несущей способности основания, находящегося в стабилизированном состоянии (все напряжения от внешней нагрузки восприняты скелетом грунта). Значения φ и с, полученные по методике быстрого неконсолидированного среза, используются для определения несущей способности медленно уплотняющихся водонасыщенных суглинков и глин, илов, сапропелей, заторфованных грунтов и торфов.

Полевое испытание на срез в заданной плоскости целика грунта, заключенного в кольцевую обойму, аналогично лабораторному испытанию на срез в одноплоскостных срезных приборах. Испытания проводятся в шурфах, котлованах, штреках и т.д. Для получения характеристик φ и с определяют сопротивление срезу не менее чем трех целиков при различных вертикальных нагрузках. Схемы испытаний принимаются те же, что и в лабораторных условиях. Значения φ и с находят на основе построения зависимости (1.5), как это показано на рис. 1.5.

Полевое определение характеристик φ и с в стенах буровой скважины проводится методами кольцевого и поступательного среза. Эти методы применяются для испытаний грунтов на глубинах до 10 м (кольцевой срез) и до 20 м (поступательный срез). В методе кольцевого среза используется распорный штамп с продольными лопастями, в методе поступательного среза — с поперечными лопастями. Метод вращательного среза с помощью крыльчатки, вдавливаемой в массив грунта или в забой буровой скважины, позволяет определить сопротивление срезу τ, поэтому его рекомендуется применять при слабых пылевато-глинистых грунтах, илах, сапропелях, заторфованных грунтах и торфах, так как для них угол внутреннего трения практически равен нулю и можно принять с = τ. Испытания крыльчаткой проводят на 
17>7>40>20>4>

  1   2   3   4   5   6

---

23. Расчетные модели оснований

Для учета изменения сопротивления грунтовых оснований по мере деформирования пользуются расчетными моделями. Наибольшее распространение имеют следующие модели и соответствующие им гипотезы:

гипотеза Фусса — Винклера (или гипотеза коэффициента постели). Грунтрассматривается как система опирающихся на жесткое горизонтальное основание и не связанных между собой пружин, сжатие которых возрастает прямо пропорционально приложенной нагрузке. Коэффициент пропорциональности между нагрузкой и деформацией называется коэффициентом постели.

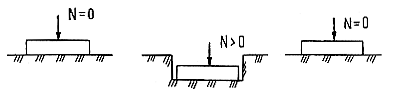
Таким образом, сопротивление грунта развивается только непосредственно под нагрузкой и в этом сопротивлении не участвует грунт, расположенный сбоку, который не испытывает осадки.
Основным недостатком данной модели является то, что поверхность грунта, как показывают эксперименты, оседает не только непосредственно под штампом (фундаментом), но и вокруг него;

модель линейно-деформируемого полупространства. Грунт рассматривается как сплошное однородное линейно-деформируемое тело, бесконечно простирающееся вглубь и в стороны и ограниченное сверху плоскостью.
В этом случае в сопротивление внешней нагрузке вовлекается все полупространство, и поэтому осадка поверхности полупространства происходит также и сбоку от места приложения нагрузки, распространяясь на большие расстояния

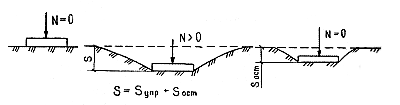
В расчет вводится не полупространство, а лишь его верхний слой, ниже которого грунт считается несжимаемым Такая модель основания принимается в тех случаях, когда на некоторой глубине залегают скальные породы или слабосжимаемые грунты. Практически за такое основание можно принимать грунты с модулем деформации Е≥100 МПа;

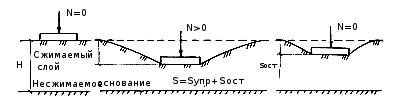
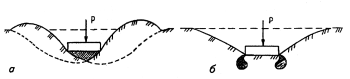
модель среды теории предельного равновесия (модель среды теории пластичности). Эта модель основана на предположении, что во всех точках грунтовой среды имеются площадки, по которым выполняется условие предельного равновесия. В этой модели принимается положение, что во всех точках грунтовой среды возникает начало состояния предельного равновесия, начало развития пластических деформаций. На рис. 6.13,априведена модель основания, работающего в условиях предельного равновесия;

---

модель упруго-пластической среды (смешанная модель теории линейно-деформируемой среды и среды теории предельного равновесия). Эта модель является синтезом двух выше рассматриваемых моделей. Данная модель предполагает наличие в грунтовой среде как области среды теории линейно-деформируемого тела, так и области состояния предельного равновесия (см. рис. 6.13,б).



30. скорость фильтрации.закон дарси

З-н Дарси, расход воды в единицу времени через единицу площади поперечного сечения грунта, или так называемая скорость фильтрации U_f, прямо пропорционален гидравлическому градиенту i, т.е. U_f= k_f * i, где k_f – коэффициент фильтрации, равный скорости фильтрации при градиенте, равном единице. Экспериментальная зависимость скорости фильтрации от гидравлического градиента носит название закона ламирной фильтрации. 

Скорости фильтрации - количество профильтровавшийся жидкости в единицу времени на единицу площади, или аналитически:

Зная скорость фильтрации, не трудно дать определение коэффициенту фильтрации:

K_ф– коэффициент фильтрации – это скорость фильтрации при I = 1 (см/сек; м/сут).

Коэффициент фильтрации для различных грунтов имеет значительный диапазон изменений, так средние значения K_ф для песков и глин может отличаться на несколько порядков (см. ниже).

K_{ф.песок}= n 10^–2см/сек

K_{ф.глина}= n 10^–8см/сек
31. закон уплотнения

Если изменения давлений будут бесконечно малым, то изменения коэффициента пористости будут строго(точно) пропорциональны изменению давления: de = - m₀ dp. Полученное соотношение имеет особо важное значение в механике грунтов и кладется в основу установления ряда ее фундаментальных положений: принципа линейной деформируемости, принципа гидроемкости, дифференциального уравнения консолидации и др. и называется законом уплотнения грунтов.

Закон уплотнения грунтов – бесконечно малое изменение относительного объема пор грунта прямо пропорционально бесконечно малому изменению давления. Или может по другому: При небольших изменениях уплотняющих давлений изменение коэффициента пористости прямо пропорционально изменению давления.

---

Смотрите также файлы

• 1. Понятие социализации личности.docx

• Лабораторная работа Проверка работы мультиметра Выполнил студент группы бтс117 Честнов И. И. 2020 лабораторная работа.docx

• Рабочая программа учебной дисциплины оп. 04 Электротехника и электронная техника по специальности 35. 02. 07 Механизация сельского хозяйства.doc

• Учебное пособие Томск 2001 удк.doc

• Причины деформации правосознания граждан.docx