Файл: Отчет По дисциплине Математическая логика и теория алгоритмов.docx
Добавлен: 26.10.2023
Просмотров: 185
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской ФедерацииФедеральное государственное бюджетное образовательноеучреждение высшего образованияТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМУПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)Кафедра автоматизированных систем управления (АСУ)ОтчетПо дисциплине «Математическая логика и теория алгоритмов»Контрольная работа №2 Вариант 11
Томск 2023Содержание1. Введение……………………………………………………...…………………32. Задача № 1……………………………………………….………………………43. Задача № 2……………………………………………….………………………44. Задача № 3…………………………………………………….…………………55. Задача № 4……………………………………………………….………………66. Задача № 5………………………………………………………….……………67. Задача № 6…………………………………………………………….…………78. Задача №7……………………………………………………………….………79. Задача № 8………………………………………………………….……………810. Заключение………………..……………………………...………………..…1111. Список использованной литературы…………………...……...……………12ВведениеКонтрольная работа №2 по дисциплине «Математическая логика и теория алгоритмов» для практического освоения задач по темам: 1) «операции с множествами», 2) «отношения», 3) «отображения», 4) «эквивалентность и порядок», 5) «логика высказываний», 6) «язык логики предикатов», 7) «математическая индукция», 8) «сравнение скорости роста».Задача №1. Проверить для произвольных множеств, чтоДокажем, что заданная равносильность не выполняется в общем случае. Возьмём множества таким образом, чтобы выполнялось: 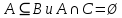. Можно представить множества кругами Эйлера:
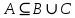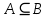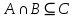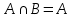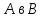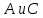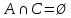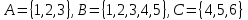
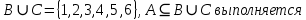
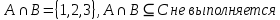
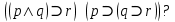
B C AВидим, что в этом случае выполняется , поскольку . С другой стороны, условие не выполняется, поскольку ввиду включения множества и ввиду того, что множества не пересекаются ( ).Построим пример:В этом случае:Таким образом, для произвольных множеств (в общем случае) не выполняется .Задача №2. Является ли тавтологией формула Нам нужно проверить равносильность левой и правой частей формулы. Левая часть формулы: 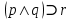. Импликация ложна только в случае, когда из истины следует ложь, поэтому 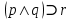принимает значение “ложь” только в случае, когда 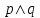принимает значение “истина”, а 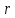- значение “ложь”. Конъюнкция 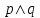принимает значение “истина” только при истинности 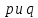. Получаем, что 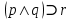принимает значение “ложь” только на одном наборе переменных:
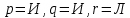.Правая часть формулы: 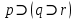. Так как импликация ложна только в случае, когда из истины следует ложь, то 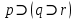принимает значение “ложь” только в случае, когда 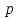принимает значение “истина”, а 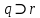- значение “ложь”. В свою очередь, 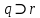принимает значение “ложь” только в случае истинности 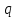и ложности . Получаем, что принимает значение “ложь” тоже на одном наборе переменных: .Видим, что обе части заданной формулы принимают значение “ложь” на одних и тех же наборах переменных (в данном случае на одном наборе). Значит, они принимают и значение “истина” на одних и тех же наборах переменных. Следовательно, эти части эквивалентны, и формула является тавтологией.Задача №3. Переведите с естественного языка на язык логики предикатов: “Всякое чётное число, большее 2, есть сумма двух простых чисел.”Универсум: множество натуральных чисел.Предикаты:Формула:Задача №4. Переведите с естественного языка на язык логики предикатов: “Хотя 60 делится на 2, 3, 4, 5 и 6, но это не значит, что 60 делится на любое натуральное число.”
Вводим два универсальных множества: множество натуральных чисел, Предикаты:Формула строим в смысловом отношении следующим образом: 60 делится на любое число из множества , но существует такое натуральное число, на которое число 60 не делится.Задача №5. Для бинарного отношения ( - множества из целых чисел) выясните, какими свойствами оно обладает (рефлексивность, симметричность, антисимметричность, транзитивность) и какими не обладает.Не для любого множества из целых чисел выполняется : для непустых множеств . Значит, отношение не является рефлексивным.Симметричность отношения ρ: из того, что следует , т.е. из следует . Отношение симметрично.Отношение не антисимметрично: если , то отсюда не следует, что Например, .Отношение не транзитивно: если
| | Выполнил: Студент гр. _______________ / «____»_______________2023г. |
| | Проверил: ______________ / «____»_______________2023г. |
B C AВидим, что в этом случае выполняется , поскольку . С другой стороны, условие не выполняется, поскольку ввиду включения множества и ввиду того, что множества не пересекаются ( ).Построим пример:В этом случае:Таким образом, для произвольных множеств (в общем случае) не выполняется .Задача №2. Является ли тавтологией формула Нам нужно проверить равносильность левой и правой частей формулы. Левая часть формулы: . Импликация ложна только в случае, когда из истины следует ложь, поэтому принимает значение “ложь” только в случае, когда принимает значение “истина”, а - значение “ложь”. Конъюнкция принимает значение “истина” только при истинности . Получаем, что принимает значение “ложь” только на одном наборе переменных:
.Правая часть формулы: . Так как импликация ложна только в случае, когда из истины следует ложь, то принимает значение “ложь” только в случае, когда принимает значение “истина”, а - значение “ложь”. В свою очередь, принимает значение “ложь” только в случае истинности и ложности . Получаем, что 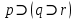принимает значение “ложь” тоже на одном наборе переменных: 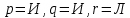.Видим, что обе части заданной формулы принимают значение “ложь” на одних и тех же наборах переменных (в данном случае на одном наборе). Значит, они принимают и значение “истина” на одних и тех же наборах переменных. Следовательно, эти части эквивалентны, и формула 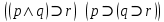является тавтологией.Задача №3. 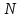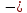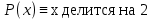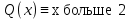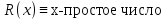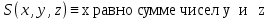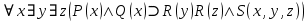Переведите с естественного языка на язык логики предикатов: “Всякое чётное число, большее 2, есть сумма двух простых чисел.”Универсум: множество натуральных чисел.Предикаты:Формула:Задача №4. Переведите с естественного языка на язык логики предикатов: “Хотя 60 делится на 2, 3, 4, 5 и 6, но это не значит, что 60 делится на любое натуральное число.”
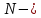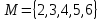
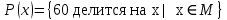
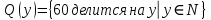
Вводим два универсальных множества: множество натуральных чисел, Предикаты:Формула строим в смысловом отношении следующим образом: 60 делится на любое число из множества 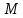, но существует такое натуральное число, на которое число 60 не делится.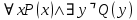Задача №5. Для бинарного отношения 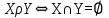( 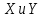- множества из целых чисел) выясните, какими свойствами оно обладает (рефлексивность, симметричность, антисимметричность, транзитивность) и какими не обладает.Не для любого множества из целых чисел 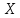выполняется 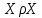: для непустых множеств 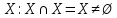. Значит, отношение 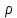не является рефлексивным.Симметричность отношения ρ: из того, что 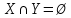следует 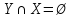, т.е. из 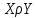следует 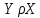. Отношение 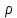симметрично.Отношение 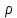не антисимметрично: если 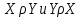, то отсюда не следует, что 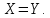Например, 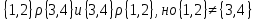.Отношение 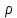не транзитивно: если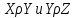
, то отсюда не следует, что 
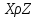. Например, 
.
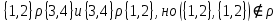Таким образом, отношение 
является симметричным, но не является рефлексивным, антисимметричным и транзитивным.
Задача №6. Пусть 
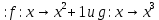- отображения 
.
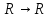Найдите отображения 
.
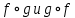Композиция отображений 
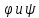следующим образом: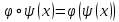
Тогда отображения :
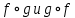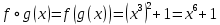
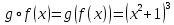
Задача №7. Используя математическую индукцию, докажите для целого 
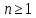, что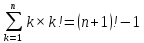 
Проверим выполнение для базиса индукции 
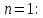
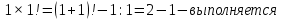
Проверим справедливость индуктивного перехода: докажем, что из справедливости равенства для 
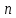следует выполнение равенства для 
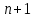. Пусть для 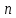равенство выполняется: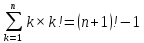
Нам нужно доказать выполнение равенства для :
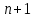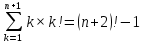
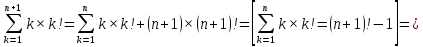
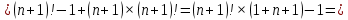
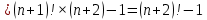
Индуктивный переход проверен.
Следовательно, для любого целого