Файл: Отчет По дисциплине Математическая логика и теория алгоритмов.docx
Добавлен: 26.10.2023
Просмотров: 45
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
выполняется:
Задача №8. Расположите следующие 5 функций в порядке увеличения скорости роста (каждая функция есть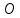
(следующая)):
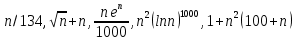
Выполняем следующие действия, не влияющие на порядок расположения функция по возрастанию скорости роста: для функции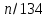
убираем постоянный множитель 
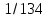; для функции 
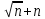оставляем слагаемое 
– с максимальной степенью ; для функции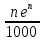 
убираем постоянный множитель 
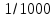; для функции 
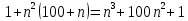оставляем слагаемое 
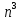– с максимальной степенью . Получаем следующий ряд функций
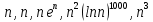
Функцию учитываем один раз (соответствующие функции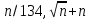 
имеют один порядок скорости роста), далее предположительно выстраиваем функции в следующем порядке (при сравнении 
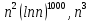считаем, что здесь большая степень существеннее, чем множитель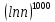 
; а функции 
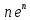имеет максимальную скорость как показательная, к тому же умноженная на ):
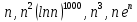
Покажем, что порядок именно такой, беря предел отношения функций (текущей к последующей) и убеждаясь, что он равен нулю. При необходимости будем переходить к непрерывному аргументу
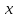и пользоваться правилом Лопиталя.
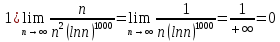
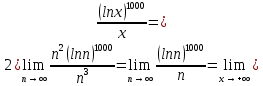
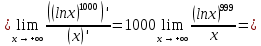
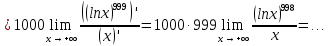
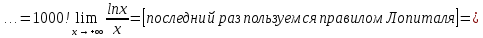
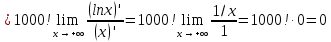
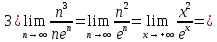
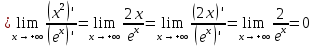
Возвращаемся к исходным функциям и располагаем их в порядке увеличения скорости роста:
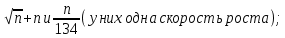
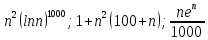
Заключение
В ходе изучения дисциплины «Математическая логика и теория алгоритмов» был освоен формальный язык математической логики для математических утверждений, базовые понятия теории множеств, а также усвоили теорию и методы математической логики и теории алгоритмов. Благодаря Контрольной работе №2 полученные знания были отработаны на практике.
Список использованной литературы:
Задача №8. Расположите следующие 5 функций в порядке увеличения скорости роста (каждая функция есть
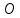(следующая)):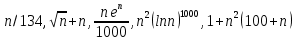 Выполняем следующие действия, не влияющие на порядок расположения функция по возрастанию скорости роста: для функции
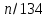убираем постоянный множитель 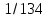; для функции 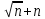оставляем слагаемое – с максимальной степенью ; для функции 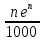убираем постоянный множитель 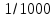; для функции 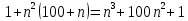оставляем слагаемое 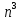– с максимальной степенью . Получаем следующий ряд функций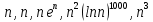 Функцию
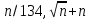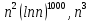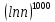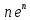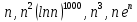
учитываем один раз (соответствующие функции имеют один порядок скорости роста), далее предположительно выстраиваем функции в следующем порядке (при сравнении считаем, что здесь большая степень существеннее, чем множитель ; а функции имеет максимальную скорость как показательная, к тому же умноженная на ): Покажем, что порядок именно такой, беря предел отношения функций (текущей к последующей) и убеждаясь, что он равен нулю. При необходимости будем переходить к непрерывному аргументу
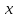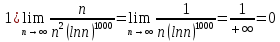
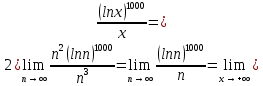
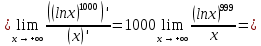
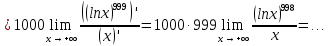
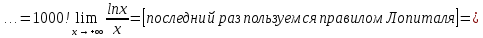
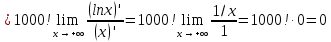
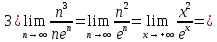
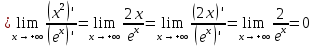
и пользоваться правилом Лопиталя. Возвращаемся к исходным функциям и располагаем их в порядке увеличения скорости роста:
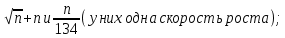
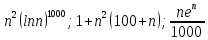
Заключение
В ходе изучения дисциплины «Математическая логика и теория алгоритмов» был освоен формальный язык математической логики для математических утверждений, базовые понятия теории множеств, а также усвоили теорию и методы математической логики и теории алгоритмов. Благодаря Контрольной работе №2 полученные знания были отработаны на практике.
Список использованной литературы:
-
Зюзьков В.М. Математическая логика и теория алгоритмов: учебное методическое пособие. — Томск: Факультет дистанционного обучения, ТУСУР, 2015. — 80 с. -
Зюзьков В.М. Математическая логика и теория алгоритмов: учебное пособие. — Томск : Эль Контент, 2015. — 236 с.