Файл: Методические указания по выполнению курсового проекта по профессиональному модулю.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 257
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
ПО ВЫПОЛНЕНИЮ КУРСОВОГО ПРОЕКТА
1. ОБЩИЕ ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КУРСОВЫХ РАБОТ
1.1 Порядок оформления пояснительной записки
Структура пояснительной записки
2.1. Классификация методов и средств измерения
Понятие о температуре и температурных шкалах
Измерение давления, разрежения и разности давлений
Измерение уровня жидкостей и сыпучих материалов.
Приборы для измерения расхода жидкости, газа, пара и тепла. Классификация расходомеров
При определении численных значений динамического коэффициента вязкости следует применять линейное интерполирование. В первом приближении можно считать, что динамический коэффициент вязкости не зависит от давления, а определяется лишь одной температурой.
С помощью табличных данных (табл. 3.3, 3.4) и метода интерполяции определяем значение динамического коэффициента вяз- кости.
1435 108 190 100 (1615 1435) 108 1579 108Па с
200 100
Отсюда получаем значение критерия Рейнольдса:
Re
4 1900
3,14 0,0511579 108 3600
834890
-
Выбираем максимальный расчетный перепад давления:
p p1 p2
p 1,1 1 0,1 МПа
Если задана допустимая величина потери давления pд, то ориентировочно можно принять ∆p = 2pд.
-
Определяем диаметр трубопровода при рабочей температуре t по уравнению:
D D20 [1 α 0 (t 20)] D20 Kt
где α0 - средний коэффициент линейного теплового расширения материала трубопровода; Kt - поправочный множитель на тепловое расширение (значения Kt приведены в таблице 3.5).
С помощью метода интерполяции определяем коэффициент
Ktпри температуре 190 ºС для чугуна.
K 1,0007 190 100 (1,0017 1,0007) 1,0016
t200 100
С учетом коэффициента Ktрассчитываем диаметр D:
D 511,0016 51,0816 мм
-
Диаметр расточки диафрагмы dопределяем в следующей последовательности:
а) подсчитываем значение mα из соотношения:
Таблица3.5
Поправочный множитель Kt на тепловое расширение трубопровода и
диафрагм
| Материалы | Температура, °С | |||||
| 100 | 200 | 300 | 400 | 500 | 600 | |
| Сталь марок 20, 20Н, 15М, 15ХМ, 12МХ | 1,0009 | 1,0021 | 1,0036 | 1,0050 | 1,0066 | 1,0082 |
| Сталь марок Х23Н13, Х18Н25С2 | 1,0010 | 1,0025 | 1,0045 | 1,0066 | 1,0081 | 1,0093 |
| Сталь марки 1Х18Н9Т | 1,0012 | 1,0029 | 1,0048 | 1,0066 | 1,0082 | 1,0099 |
| Бронза | 1,0014 | 1,0031 | 1,0050 | 1,0069 | 1,0091 | - |
| Чугун | 1,0007 | 1,0017 | 1,0030 | 1,0044 | 1,0060 | - |
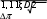 mα G
mα GВеличину s берут из таблицы 3.6 по подсчитанному значе- нию ∆p/p1 принимая m=0,3 (в первом приближении).
Сначала находим соотношение ∆p/p1:
p 0,1 0,091
p1 1,1
Затем методом интерполяции определяем значение ε:
ε 0,973 0,091 0,08 (0,973 0,944) 0,969
0,16 0,08
Таблица 3.6
Значение поправочного множителя на расширение среды, s
| | Х=1,3 | Х=1,4 | ||||||
| m=0 | m=0,3 | m=0,5 | m=0,7 | m=0 | m=0,3 | m=0,5 | m=0,7 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0,02 | 0,994 | 0,993 | 0,992 | 0,991 | 0,994 | 0,993 | 0,992 | 0,991 |
| 0,04 | 0,988 | 0,987 | 0,985 | 0,983 | 0,988 | 0,987 | 0,985 | 0,983 |
| 0,08 | 0,975 | 0,973 | 0,969 | 0,964 | 0,976 | 0,974 | 0,970 | 0,965 |
| 0,16 | 0,948 | 0,944 | 0,936 | 0,926 | 0,950 | 0,946 | 0,938 | 0,929 |
| 0,32 | 0,895 | 0,887 | 0,831 | 0,850 | 0,900 | 0,892 | 0,876 | 0,855 |
Исходя из вышеприведенной формулы, вычисляем величину mα:
mα
1900
0,2355
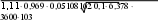 б) для найденного значения mα находят величину m.
б) для найденного значения mα находят величину m.Для нахождения значения mпо известной величине mα строим графическую зависимость mα = ƒ(m) при принятом значении D.
Для этого по данным таблицы 3.7 берем четыре соответствующих значения m и mα, которые представлены в табл. 3.8, и строим график mα = ƒ(m) . Для определения значений mα проводим интерполяцию, так как диаметр трубопровода отличается от указанного в таблице (выбираем четыре точки так, чтобы две имели значение mα больше и две меньше, чем получилось при расчете по формуле).
Таблица 3. 7

| m | | |||
| ≥300 | | | 50 | |
| 0,05 | 0,03005 | 0,03020 | 0,03047 | 0,03065 |
| 0,075 | 0,04508 | 0,04541 | 0,04581 | 0,04610 |
| 0,1 | 0,06038 | 0,06070 | 0,06123 | 0,06265 |
| 0,125 | 0,07578 | 0,07618 | 0,07668 | 0,07740 |
| 0,15 | 0,0913 | 0,0918 | 0,0926 | 0,0933 |
| 0,2 | 0,1231 | 0,1237 | 0,1248 | 0,1258 |
| 0,25 | 0,1560 | 0,1567 | 0,1582 | 0,1597 |
| 0,3 | 0,1902 | 0,1910 | 0,1929 | 0,1948 |
| 0,35 | 0,2257 | 0,2268 | 0,2289 | 0,2314 |
| 0,4 | 0,2640 | 0,2652 | 0,2678 | 0,2707 |
| 0,45 | 0,3042 | 0,3056 | 0,3088 | 0,3021 |
| 0,5 | 0,3475 | 0,3492 | 0,3530 | 0,3569 |
| 0,55 | 0,3938 | 0,3960 | 0,4003 | 0,4048 |
| 0,6 | 0,4440 | 0,4467 | 0,4517 | 0,4569 |
| 0,65 | 0,4992 | 0,5024 | 0,5082 | 0,5112 |
| 0,7 | 0,5614 | 0,5653 | 0,5720 | 0,5788 |
Зависимость произведения ma от m и D
200
D, мм
100
По построенному графику определяют численное значение
m. Величину m рекомендуется определять с числом значащих цифр, соответствующих погрешности порядка 0,1%.
При m =0,2355 значение m=0,355.
в) определяем предварительное значение диаметра расточки
диафрагмы при температуре 20°С из соотношения:
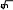 d20 D20
d20 D20 d20 51
d20 510,355 30,39мм
Таблица 3. 8
Зависимость произведения ma от m
| m | 0,25 | 0,3 | 0,35 | 0,4 |
| m | 0,1596 | 0,1947 | 0,23125 | 0,27053 |
-
Определяем потерю напора в диафрагме при расчетном
расходе из соотношения:
p Kp, МПа
где К - коэффициент, являющийся функцией от m(см. табл. 3.9).
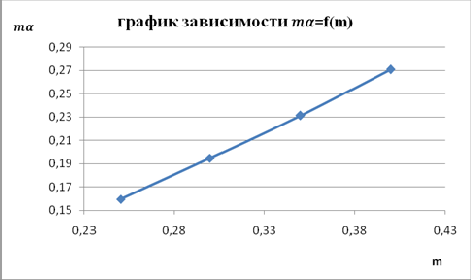
Рис. 20. График зависимости mα=f(m)
Таблица 3. 9
Значения коэффициента К в зависимости от величины m
| m | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| К | 1 | 0,88 | 0,78 | 0,68 | 0,57 | 0,47 | 0,37 | 0,27 |
Применив метод интерполяции, получаем:
K 0,57 0.355 0,3 (0,68,057) 0,6305
0,4 0,3
Таким образом, потеря напора в диафрагме составит:
p 0,6305100000 63050Па
-
Проверка определения диаметра расточки отверстия диа- фрагмы dзаключается в следующем:
а) Из представленного ниже соотношения определяется ко- эффициент расхода:
α αuK1K2 K3
где αu – исходный коэффициент расхода; К1 ‒ поправочный множи- тель, который вводится при значении Re меньше предельного; К2 ‒ поправочный множитель на относительную шероховатость труб; К3
‒ поправочный множитель на неостроту входной кромки.
б). Подсчитываем значение α. Для этого по расчетному зна- чению m, пользуясь таблицей 3.10, определяем величину исходного коэффициента расхода αu с точностью не менее третьего знака (применяя интерполирование в промежутке).
Таблица 3.10
Значение исходного коэффициента расхода au и предельные значения критериев Рейнольдса (Reпред)
| m | αu | Reпред |
| 0,05 | 0,598 | 23000 |
| 0,1 | 0,602 | 30000 |
| 0,15 | 0,608 | 45000 |
| 0,2 | 0,615 | 57000 |
| 0,25 | 0,624 | 75000 |
| 0,3 | 0,634 | 93000 |
| 0,35 | 0,645 | 110000 |
| 0,4 | 0,66 | 130000 |
| 0,45 | 0,676 | 160000 |
| 0,5 | 0,695 | 185000 |
| 0,55 | 0,716 | 210000 |
| 0,6 | 0,74 | 240000 |
| 0,65 | 0,768 | 270000 |
0,634 0,355 0,35 (0,66 0,645) 0,6465
u 0,4 0,35
в). Определяем предельное значение критерия Рейнольдса:
Re пред
93000 0,355 0,35 (130000 110000) 112000
0,4 0,35