Файл: Типовой расчет 1 оценка статистических характеристик случайных данных.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 26.10.2023

Просмотров: 39

Скачиваний: 5

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ТИПОВОЙ РАСЧЕТ №1 «ОЦЕНКА СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ДАННЫХ»

По статистическим данным, полученным в результате проведения опыта, требуется:

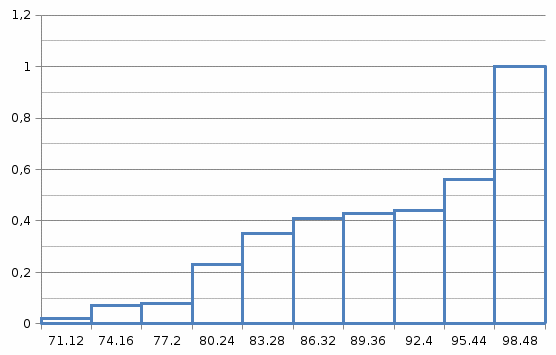
  1. Произвести группировку, построить гистрограмму интервального ряда и изобразить график статистического распределения относительных частот.

  2. Найти эмпирическую функцию распределения, взяв за варианты середины найденных интервалов и построить ее график.

  3. Вычислить выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, моду, медиану.

  4. С вероятностью 0,99 найти доверительный интервал для истинного значения рассматириваемой величины.

  5. Построить теоретическую нормальную кривую.

  6. Предполагая о нормальном распределении генеральной совокупности и пользуясь критерием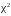 на уровне значимости 0,01, установить случайно или значимо расхождение между формой распределения выборки и генеральной совокупности.

Порядок выполнения задания

  1. Провести группировку выборки, разбив весь интервал на 10 частичных интервалов одинаковой длины hxmaxxmin/10 и подсчитать, сколько значений признака попадает в каждый частичный интервал (значения, совпадающие с граничными, следует отнести к левому интервалу).

  2. Построить эмпирическую функцию распределения по формуле

,

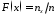где 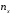- число вариант меньших х.

  1. Статистические оценки параметров распределение провести по формулам





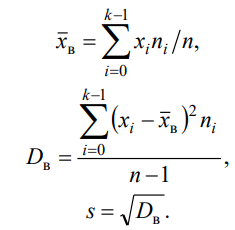
  1. Найти доверительный интервал для математического ожидания mx из неравенств



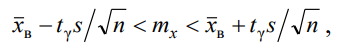
где ty(v) - параметр, значения которого берется из таблицы в зависимости от объема выборки
и надежности 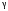; Число степеней свободы v определяется как объем выборки n минус количество параметров d в принятом распределении ( v  n  d ). Доверительный интервал для среднего квадратического отклонения σ найти по формуле

s(1-q) < σ < s(1+q), при q<1

0 < σ < s(1+q), при q>1,

  1. Построить нормальную кривую.

  2. Вычислить значение критерия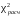



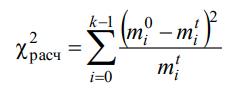
здесь mi0- наблюдаемые частоты для каждой группы, mit- теоретические частоты, вычисленные в предположении о нормальности распределения.

Теоретические частоты для каждой группы рассчитываются по формуле



где i p вероятность попадания в группу определяется как разность значений функции распределения между границами соответствующей группы. Для этого исходные границы групп нормируются и центрируются с использованием формулы



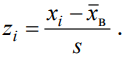
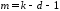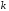В заключение расчетная величина критерия xрасч2 сравнивается с табличным значением xкр2 для заданного уровня значимости и числа степеней свободы , где – количество групп после объединения, если она оказалась необходимой (в группах частоты должны быть больше 5), 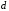– количество параметров определенных по выборке для нахождения теоретических частот (для нормального распределения ) .

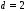Если xрасч2 < xкр2, то гипотеза о нормальном распределении принимается. А если xрасч2 > xкр2, то гипотеза отклоняется.


83.5
95.9
100
84.6
80.7
75.4
80.1
97.1
96.1
99.1

84.8
100
100
80.8
79.2
71.2
90.5
100
96.9
99.7

82.3
100
100
88.9
81
79.8
84.8
100
96.1
100

82
100
100
79.8
79.7
81.9
90.9
100
96.9
98.8

85.7
100
100
84.6
81.3
73.4
94.7
100
96.8
99.3

87.6
100
100
87.4
79.5
86.7
100
100
94
99.4

87.7
100
100
84.6
80
73.2
99
100
100
99

85.5
100
100
81.7
83.6
75.6
97.1
99.4
100
99.3

84.2
100
94.4
76.5
81.3
69.6
96.5
100
99.6
100

95.9
100
84.6
80.7
75.4
80.1
97.1
96.1
99.1
100

  1. Провести группировку выборки, разбив весь интервал на 10 частичных интервалов одинаковой длины h  xmax  xmin /10 и подсчитать, сколько значений признака попадает в каждый частичный интервал (значения, совпадающие с граничными, следует отнести к левому интервалу).

xmax = 100

xmin = 69.6


h  xmax  xmin /10= 3.04

ni =2 5 1 15 12 6 2 1 12 44

x=69.6000 72.6400 75.6800 78.7200 81.7600 84.8000 87.8400 90.8800 93.9200 96.9600 100.0000


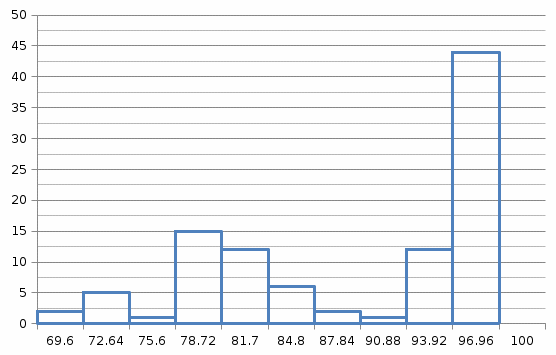
Xi=71.1200 74.1600 77.2000 80.2400 83.2800 86.3200 89.3600 92.4000 95.4400 98.4800



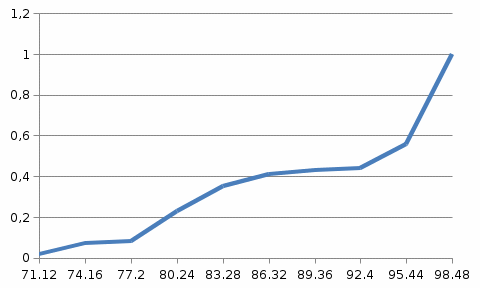
2.Построить эмпирическую функцию распределения по формуле

, где - число вариант меньших х.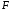

0.02

0.07
0.08
0.23

0.35
0.41
0.43
0.44
0.56

1



3.Статистические оценки параметров распределение провести по формулам

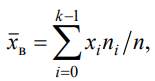= 90.6

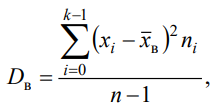=76.72

=8.75

4.Найти доверительный интервал для математического ожидания 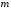из неравенств



Ty(v) - параметр, значения которого берется из таблицы в зависимости от объема выборки и надежности . Число степеней свободы v определяется как объем выборки n минус количество параметров d в принятом распределении ( v  n  d ). Доверительный интервал для среднего квадратического отклонения σ найти по формуле

s(1-q) < σ < s(1+q), при q<1

88.1809 < m < 93.0318

5.Построить нормальную кривую.

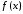0.0047

0.0088
0.0151
0.0230
0.0315
0.0388
0.0428
0.0424
0.0377
0.0300



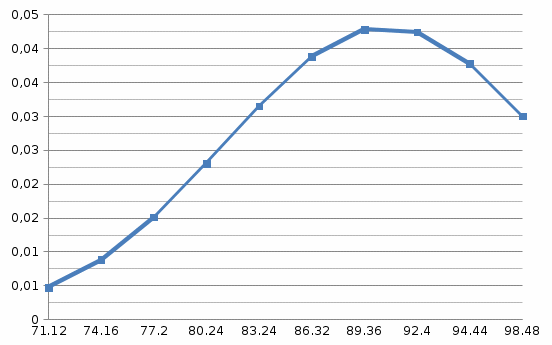
6.Вычислить значение критерия



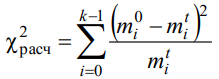
здесь mi0 – наблюдаемые частоты для каждой группы, mit – теоретические частоты, вычисленные в предположении о нормальности распределения. Теоретические частоты для каждой группы рассчитываются по формуле



где pi вероятность попадания в группу определяется как разность значений функции распределения между границами соответствующей группы. Для этого исходные границы групп нормируются и центрируются с использованием формулы



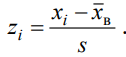
В заключение расчетная величина критерия xрасч2 сравнивается с табличным значением xкр2 для заданного уровня значимости и числа степеней свободы m=k-d-1, где – количество групп после объединения, если она оказалась необходимой (в группах частоты должны быть больше 5), d – количество параметров, определенных по выборке, для нахождения теоретических частот (для нормального распределения d  2 ).

xрасч2 < xкр2



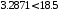
гипотеза о нормальном распределении принимается.

Смотрите также файлы