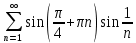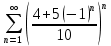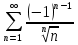Практическое заданиепо дисциплине «Математика»

ФИО
Направление	09.03.03. Прикладная информатика

Москва 2023г.Практическое задание по дисциплине
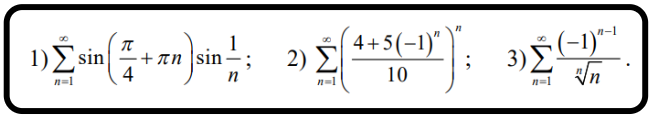
«Математика»Задание 1. Выясните, сходятся данные ряды абсолютно, условно или же расходятся.Решение:

1. 
   
   

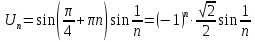
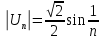
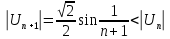
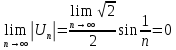
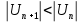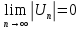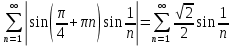
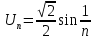
Это знакочередующий ряд. Исследуем его по теореме ЛейбницаТ.к. и - то по теореме Лейбница ряд сходитсяИсследуем на сходимость ряд, составленный из абсолютных величин членов данного ряда, чтобы узнать, сходится исходный ряд абсолютно или условно.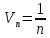- общий член гармонического ряда. Гармонический ряд расходится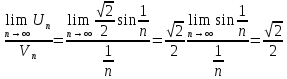По предельному признаку сравнения ряд 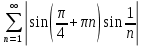расходится. Значит исходный ряд сходится условно.Ответ: ряд сходится условно.

2. 
   
   

Это знакочередующий ряд. Исследуем на сходимость ряд, составляенный из абсолютных величин членов данного ряда. Если он сходится – то и данный ряд сходится, причем абсолютно.

---

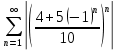
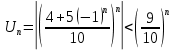
Ряд 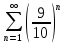- это ряд геометрической прогрессии 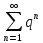, он сходится при 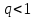. В данном случае: 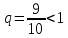– ряд сходитсяПо признаку сравнения ряд 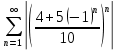сходитсяЗначит исходный ряд сходится абсолютноОтвет: ряд сходится абсолютно

3. 
   
   

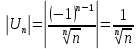
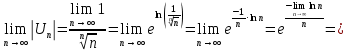
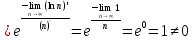
Это знакочередующий ряд. Необходимый признак сходимости ряда не выполняется. Ряд расходится.Ответ: ряд расходится.Задание 2. Выпущено 900 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на 10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 50 – выигрыш в 10 рублей. Определить закон распределения вероятностей случайной величины X – выигрыша на один билет. Для определения закона распределения вероятностей случайной величины X, необходимо вычислить вероятности каждого возможного выигрыша и его стоимость, а затем свести эти данные в таблицу.Пусть X – случайная величина, представляющая выигрыш на один лотерейный билет. Тогда возможны следующие значения X и соответствующие им вероятности:X = 500 рублей, вероятность P(X = 500) = 5/900 = 1/180X = 100 рублей, вероятность P(X = 100) = 10/900 = 1/90X = 50 рублей, вероятность P(X = 50) = 20/900 = 2/90X = 10 рублей, вероятность P(X = 10) = 50/900 = 1/18X = 0 рублей (нет выигрыша), вероятность P(X = 0) = 815/900 = 163/180Таблица закона распределения вероятностей случайной величины X будет выглядеть следующим образом:

Значения Х	0	10	50	100	500
Вероятности Р	163/180	1/18	2/90	1/90	1/180

---

Смотрите также файлы

• Баллов 1,0 из 1,0 На рисунке представлен график, на котором отражен выпуск продукции фирмы в условиях совершенной конкуренции.pdf

• 1. 11. Требования к безопасности досуговых мероприятий и массовых досуговых мероприятий.odt

• Краткое содержание работы Срок выполнения 1 2 3 4.docx

• Лист по проведению инструктажа обучающихся по ознакомлению с требованиями охраны труда, техники безопасности, пожарной безопасности и правилами внутреннего трудового распорядка.doc

• Вместе мы! Командир Кто имеет доброе сердце Вместе.docx