Файл: Бином Ньютона формула разложения произвольной натуральной степени двучлена.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 53
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Бином Ньютона
Бином Ньютона — формула разложения произвольной натуральной степени двучлена (a+b)n в многочлен. Каждый из нас знает наизусть формулы «квадрата суммы» (a+b)2 и «куба суммы» (a+b)3, но при увеличении показателя степени с определением коэффициентов при членах многочлена начинаются трудности. Чтобы не совершить ошибку и применяется формула бинома Ньютона:

где k - порядковый номер слагаемого в многочлене.
Видно, что в любом многочлене присутствуют an и bn с коэффициентами 1. Ясно также, что всякий иной член многочлена выглядит как произведение определённых степеней каждого из слагаемых двучлена (a+b), причём сумма степеней всегда равна n. Например, в выражении
(a+b)3=a3+3a2b+3ab2+b3
сумма степеней сомножителей во всех членах равна трём (3, 2+1, 1+2, 3). То же самое справедливо и для любой другой степени.
Чтобы правильно расставить коэффициенты при каждом элементе пользуются треугольником Паскаля.
Строится он следующим образом. В вершине треугольника пишем 1. Единица соответствует выражению (a+b)0, поскольку любое число, возведённое в нулевую степень, даёт единицу. Достраивая треугольник, ниже пишем ещё по единице. Это коэффициенты разложения того же двучлена, возведённого в первую степень:(a+b)1=a+b. Стороны треугольника образуют единицы, а между ними — сумма двух единичек, находящихся сверху, то есть 2. Это и есть коэффициенты трёхчлена «квадрат суммы»:
a2+2ab+b2.
Следующий ряд, как и предыдущий, начинается и заканчивается единицами, а между ними — суммы цифр, находящихся сверху: 1, 3, 3, 1. Мы получили коэффициенты разложения « куба суммы ». Ряд коэффициентов двучлена четвёртой степени составят 1, 4, 6, 4, 1 и так далее.
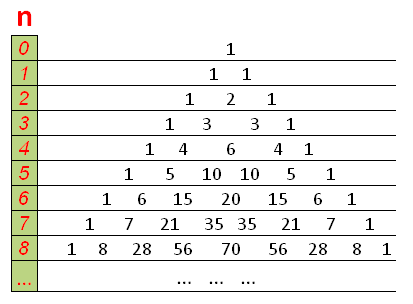
Для примера с помощью треугольника Паскаля разложим в многочлен сумму двучленов в шестой степени:
(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.
Основные свойства биноминальных коэффициентов:
-
Коэффициенты членов, равноудаленных от начала и от конца разложения бинома, равны между собой.
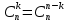
-
Коэффициент (k+1) члена разложения бинома равен произведению коэффициента k – го члена на показатель степени x в этом члене, деленному на k.
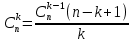
3. Сумма всех биноминальных коэффициентов равна 2n
-
Сумма биноминальных коэффициентов, стоящих на четных местах, равна сумме биноминальных коэффициентов, стоящих на нечетных местах
Пример: Написать разложение по формуле бинома Ньютона и упростить:
-
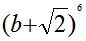 ; Ответ:
; Ответ: 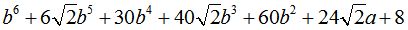 .
. -
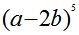 ; Ответ:
; Ответ: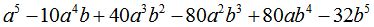 .
.