Файл: Контрольная работа По дисциплине Дискретная математика Выполнил Группа Проверил Мурзина Т. С.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 34
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Контрольная работа
По дисциплине: Дискретная математика
Выполнил:
Группа:
Проверил: Мурзина Т. С.
Новосибирск, 2012 г
-
Задано универсальное множество U и A, B, C, D множества. Найти результаты действий a) - д) и каждое действие проиллюстрировать с помощью диаграммы Эйлера-Венна.
U={10,11,12,13,14}
A={10,11,12}; B={12,13,14}; C={10,14}; D={12}
-
Ввести необходимые элементарные высказывания и записать логической формулой следующее предложение.
“Если А знаком с Б, и Б знаком с В, то либо А знаком с В, либо А не знаком с В”.
-
Для булевой функции f(x,y,z) найти методом преобразования минимальную ДНФ. По таблице истинности построить СКНФ. По минимальной ДНФ построить релейно-контактную схему.
-
Орграф задан своей матрицей смежности. Следует:
а) нарисовать орграф;
б) найти полустепени и степени вершин;
в) записать матрицу инцидентности;
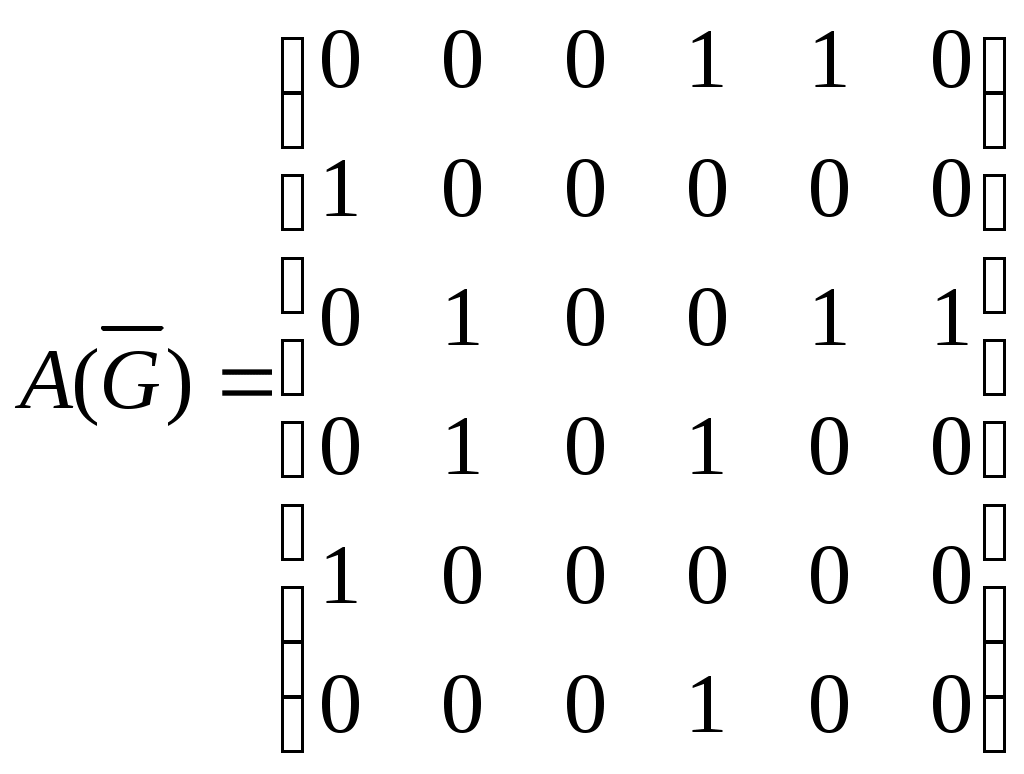
Задание 1
Задано универсальное множество U и множества A, B, C, D. Найти результаты действий a) - д) и каждое действие проиллюстрировать с помощью диаграммы Эйлера-Венна.
U = {10, 11, 12, 13, 14}.
A = {10, 11, 12}
B = {12, 13, 14}
C = {10, 14}
D = {12}
а)
б)
в)
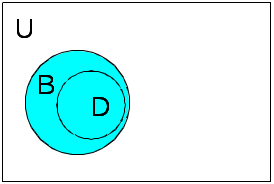
г)
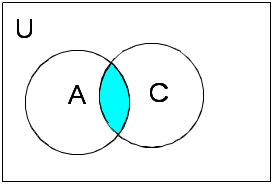
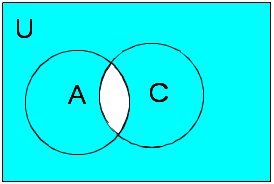
д)
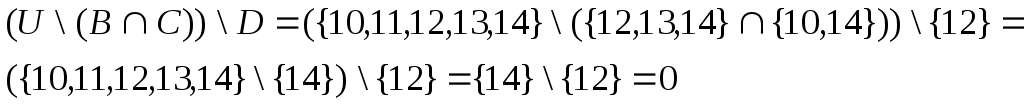
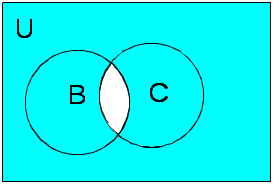
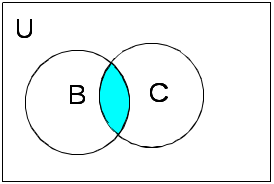
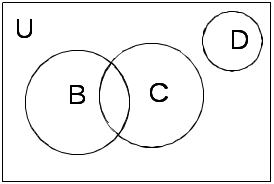
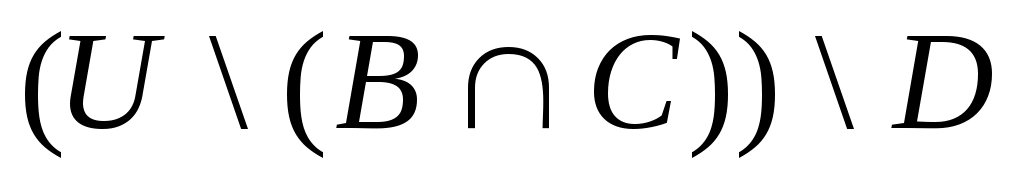
Задание 2.
Ввести необходимые элементарные высказывания и записать логической формулой следующее предложение.
7. “Если А знаком с Б, и Б знаком с В, то либо А знаком с В, либо А не знаком с В”.
А знаком с Б =
Б знаком с В =
А знаком с В =
А не знаком с В =
Речевой оборот если…., то…. в логике высказываний выполняет операция импликация. Тогда высказывание “Если А знаком с Б, и Б знаком с В, то либо А знаком с В, либо А не знаком с В” примет вид
Задание 3.
Для булевой функции
найти методом преобразования минимальную ДНФ. По таблице истинности построить СКНФ. По минимальной ДНФ построить релейно-контактную схему.7.
Для получения МДНФ выполним следующие преобразования:
Все не булевские операции заменить на булевские c помощью равносильностей:
Составим таблицу истинности для исходной формулы:
| X | Y | Z |  |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
Уберем отрицания над выражениями с помощью правила Моргана:
Применим закон поглощения и коммутативности дизъюнкции
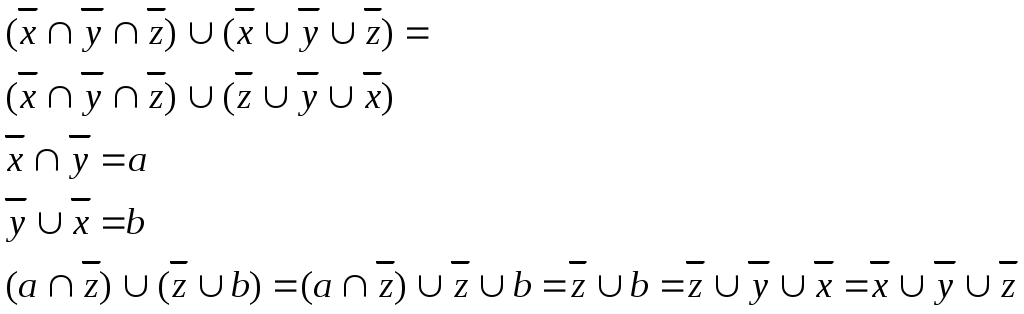
Таким образом МДНФ равна
Составим таблицу истинности для данной МДНФ
| X | Y | Z |  |  |  |  |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Построим СКНФ. Располагая таблицей истинности функции, запишем основные дизъюнкции
| X | Y | Z |  | основные дизъюнкции |
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 0 | |
Запишем СКНФ. Она составляется для тех значений F(x,y,z), которые равны нулю.
Построим релейно-контактную схему для заданной МДНФ
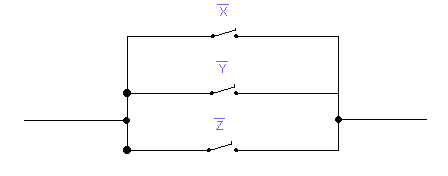
Задание 4.
Орграф задан своей матрицей смежности. Следует:
а) нарисовать орграф;
б) найти полустепени и степени вершин;
в) записать матрицу инцидентности;
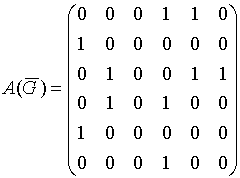
А) По матрице смежности построим соответствующий орграф. Орграф – это ориентированный граф, ребра его называются дугами, и, в отличие от графа, имеют начало и коне -то есть они направлены. В таблице смежности строки и столбцы соответствуют вершинам, единицы в матряице – это дуги – причем номер строки– это вершина, где дуга начинается, а номер столбца – это вершина, где дуга заканчивается.
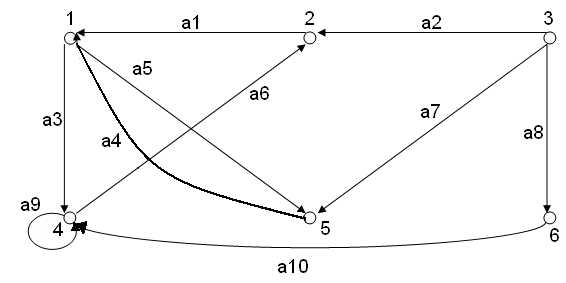
Б) Найдем полустепени и степени вершин (табл.1).
Степенью вершины называется число дуг орграфа, инцидентных данной вершине, при этом петли учитываются дважды.
Полустепени для орграфа делятся на:
Полустепени исхода – число дуг, исходящих из данной вершины;
Полустепени захода – число дуг, входящих в данную вершину.
Таблица 1. Степени и полустепени вершин.
| Вершина | Степень вершины | Полустепень вершины | |
| исхода | захода | ||
| 1 | 4 | 2 | 2 |
| 2 | 3 | 1 | 2 |
| 3 | 3 | 3 | 0 |
| 4 | 5 | 2 | 3 |
| 5 | 3 | 1 | 2 |
| 6 | 2 | 1 | 1 |