Файл: Расчетнографическая работа по дисциплине Основы технической механики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 42
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
NF lim
KFL1,2 = 6 ,
NFE1,2
где NF lim – базовое число циклов напряжений изгиба NF lim = 4 ⋅ 106;
NFE1,2 – расчетное число циклов напряжений изгиба
Расчетное число циклов напряжений изгиба определяют по формуле
NFE1,2 = KFE ⋅ [60⋅n1,2 ⋅ t] ,
где KFE – коэффициент режима работы при расчете на изгиб
NFE1 = 1 ⋅ (60 ⋅ 645,75 ⋅ 20000) = 774900000
NFE2 = 1 ⋅ (60 ⋅ 205 ⋅ 20000) = 246000000
4 ⋅ 106
KFL1 = 6 = 0,42
7749 ⋅ 105
4 ⋅ 106
KFL2 = 6 = 0,5
246 ⋅ 106
Так как KFL1,2 < 1, то принимаем KFL1,2 = 1.
2.2 Проектный расчет
Тип передачи: косозубая
Определяем межосевое расстояние по формуле
T2 ⋅ 103 ⋅ KHβ
a′w = Ka (u+1) ⋅ 3 ,
u2 ⋅ѱba ⋅ [σН ]2
где Ka – вспомогательный коэффициент: для косозубых цилиндрических колес Ka = 43 МПа1/3;
ѱba – коэффициент ширины шестерни относительно межосевого расстояния;
KHβ – коэффициент концентрации нагрузки, учитывающий неравномерное распределение нагрузки по линии контакта зубьев. Выбирается в зависимости от
ѱbd = 0,5 ⋅ ѱba ⋅ (u+1)
ѱbd = 0,5 ⋅ 0,5 ⋅ (3,15+1) = 1,03
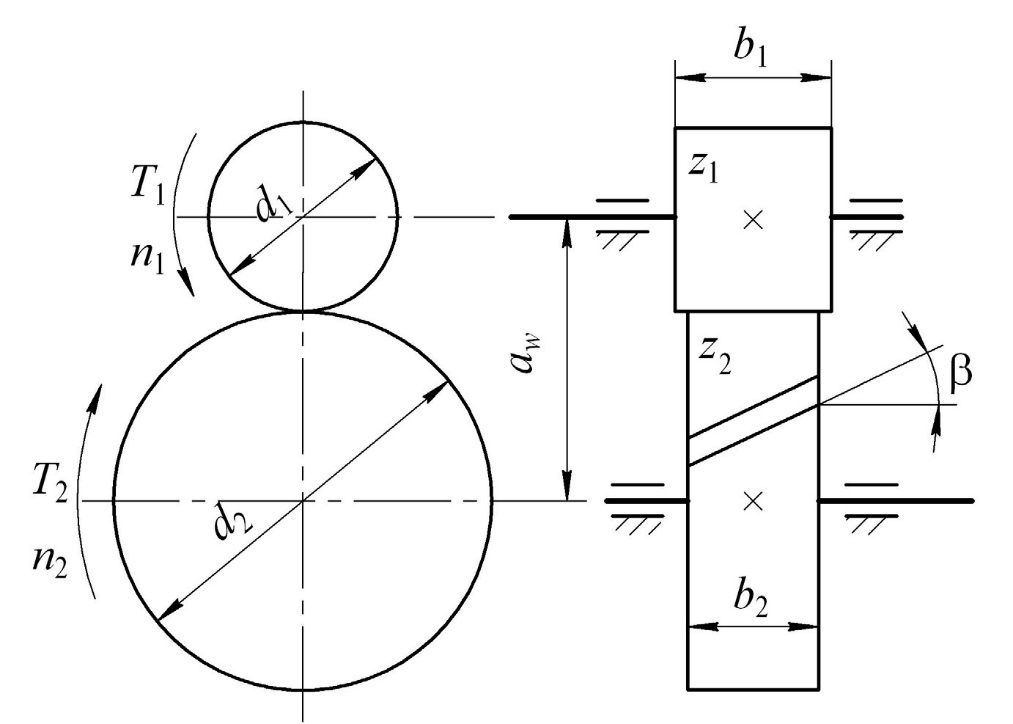
Рис. 1. Схема цилиндрической зубчатой передачи
916,38 ⋅ 103 ⋅ 1,04
a′w = 43 ⋅ (3,15+1) ⋅ 3 = 163,46 мм
3,152 ⋅ 0,5 ⋅ 5002
Полученное значение a′w округляем до стандартного межосевого расстояния aw по ГОСТ 2185-66 «Передачи зубчатые цилиндрические. Основные параметры»
Принимаем aw
= 200 мм
Определяем ширину зубчатого колеса по формуле: b′2 = ѱba ⋅ aw
b′2 = 0,5 ⋅ 200 = 100 мм
Полученное значение b′2 округляем до значения b2 по предпочтительному ряду Ra 40 по ГОСТ 6636-69
Принимаем b2 = 100 мм
Ориентировочно определяем модуль зацепления передачи по формуле
m′ = b2 / ѱm , где ѱm – коэффициент модуля
m′ = 100 / 20 = 5 мм
Полученное значение m′ округляем до стандартного значения m по ГОСТ 9563-80 «Основные нормы взаимозаменяемости. Колеса зубчатые. Модули».
Принимаем m = 5 мм
Назначаем угол наклона зубьев для шевронных колес β = 45°
Задаем направление наклона зубьев: для шестеренки – левое, для зубчатого колеса – правое.
Определяем коэффициент осевого перекрытия по формуле
εβ = (b2 ⋅ sinβ) / (π ⋅ m) ≥ 1,1
εβ = (100 ⋅ sin45°) / (3,14 ⋅ 5) = 4,52
Определяем суммарное число зубьев передачи по формуле
z∑ = 2 ⋅ aw ⋅ cosβ / m
z∑ = 2 ⋅ 200 ⋅ cos45° / 5 = 57
Определяем число зубьев шестерни z1 и колеса z2 с округлением до целого числа по формуле
z1 = z∑ / (u+1) z2 = z∑ - z1
z1 = 57 / (3,15+1) = 14 z2 = 57 – 14 = 43
Уточняем передаточное число u = z2 / z1 u = 43 / 14 = 3,07
Проверка: Δu = (3,07 – 3,15) ⋅ 100 / 3,15 = - 2,5% ≤ ±4% условие выполнено
Уточняем значение угла наклона зубьев с точностью до секунды по формуле
cosβ = [0,5 ⋅ (z1 + z2) ⋅ m] / aw
cosβ = [0,5 ⋅ (14 + 43) ⋅ 5] / 200 = 0,7125
Определяем коэффициент торцевого перекрытия по формуле
εα = [1,88 – 3,2 ⋅ (1 / z1 + 1 / z2)] ⋅ cosβ
εα = [1,88 – 3,2 ⋅ (1 / 14 + 1 / 43)] ⋅ 0,7125 = 1,12 ≥ 1,1
Определяем делительные диаметры шестерни и зубчатого колеса по формулам
d1 = m ⋅ z1 / cosβ и d2 = m ⋅ z2 / cosβ
d1 = 5 ⋅ 14 / 0,7125 = 98,25 мм d2 = 5 ⋅ 43 / 0,7125 = 301,75 мм
Определяем окружную скорость по формуле
υ = π ⋅ d1 ⋅ n1 / 60
υ = 3,14 ⋅ 98,25 ⋅ 645,75 / 60 = 3,32 м / с
Назначаем степень точности и вил сопряжения цилиндрической передачи согласно ГОСТ 1643-81 «Основные нормы взаимозаменяемости. Передачи зубчатые цилиндрические. Допуски»
Степень точности: 9-В
2.3 Проверочный расчет
По контактным напряжениям
Определяем контактные напряжения по формуле
σН = ZE ⋅ ZH ⋅ Zε ⋅ 2 ⋅ T2 ⋅ 103 ⋅ (u+1) ⋅ KH ≤ [σН ]
d22 ⋅ b2
где ZE – коэффициент, учитывающий свойства материала шестерни и колеса, ZE =275 МПа1/2;
ZH – коэффициент, учитывающий форму сопряжения поверхностей зубьев;
Zε – коэффициент, учитывающий суммарную длину контактной линии;
KH – коэффициент расчетной нагрузки при расчете на контактные напряжения.
ZH = 2 ⋅ cosβ = 2 ⋅ 0,7125 = 1,38
sin2α sin40°
Для косозубой передачи Zε = 1 = 1 = 0,94
εα 1,12
Коэффициент KH определяется как KH = KHβ ⋅ KHν ⋅ KHα
где KHβ – коэффициент концентрации нагрузки (определен ранее);
KHv – коэффициент динамичности нагрузки, учитывающий дополнительную динамическую нагрузку;
KHα – коэффициент нагрузки в зацеплении, учитывающий неравномерность распределения нагрузки между парами зубьев (только для косозубых передач);
KH = 1,04 ⋅ 1,0432 ⋅ 1,13 = 1,23
σН = 275 ⋅ 1,38 ⋅ 0,94 ⋅ 2 ⋅ 916,38 ⋅ 103 ⋅ (3,15+1) ⋅ 1,23 = 361,7 МПа ≤ [σН ] ≤ 500 МПа
301,752 ⋅ 100
Отклонение возникающего контактного напряжения от допускаемого
ΔσН = (σН - [σН ]) ⋅ 100% / σН ΔσН = (361,7 - 500) ⋅ 100% / 500 = - 27,66%
Условие прочности не выполняется, значит изменяем ширину венца колеса по формуле
b*2 = b2
⋅ (σН / [σН ])2
b*2 = 100 ⋅ (361,7 / 500)2 = 53 мм
σН* = 495,85 МПа ΔσН = (495,85 - 500) ⋅ 100% / 500 = - 0,83% ≤ ±5%
условие выполнено
По напряжениям изгиба
Определяем допускаемые напряжения изгиба по формуле
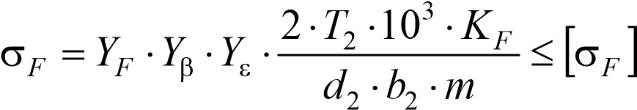
где YF – коэффициент формы зуба, зависящий от эквивалентного числа зубьев шестерни и колеса: zV1 = z1 / cos3 β и zV 2 = z2 / cos3 β
zV1 = 14 / 0,71253 = 39 YF1 = 3,71
zV2 = 43 / 0,71253 = 119 YF2 = 3,60
[σF ]1 / YF1 = 267,43 / 3,71 = 72,08 [σF ]2 / YF2 = 226,29 / 3,60 = 62,86
Принимаем YF = 3,60
Yβ – коэффициент повышения изгибной прочности зуба косозубых колес (только для косозубых передач), Yβ =1− εβ ⋅(β / 120);
Yβ =1− 4,52 ⋅ (44,36 / 120) = 0,67
Yε – коэффициент распределения нагрузки между зубьями (только для косозубых передач), Yε =1 / εα ;
Yε =1 / 1,12 = 0,89
KF – коэффициент расчетной нагрузки для напряжений изгиба.
Коэффициент KF определяется как KF = KFβ ⋅KFv ⋅KFα,
где KFβ – коэффициент концентрации нагрузки;
KFv– коэффициент динамичности нагрузки;
KFα – коэффициент нагрузки в зацеплении (только для косозубых передач)
KF = 1,09 ⋅1,1162⋅1,35 = 1,64
σF = 3,60 ⋅ 0,67 ⋅ 0,89 ⋅ (2 ⋅ 916.38 ⋅ 103 ⋅ 1,64) / (301,75 ⋅ 100 ⋅ 5) = 42,77 МПа ≤ [σF ]2 ≤ 226,29 МПа
2.4 Расчет геометрических параметров цилиндрической передачи
О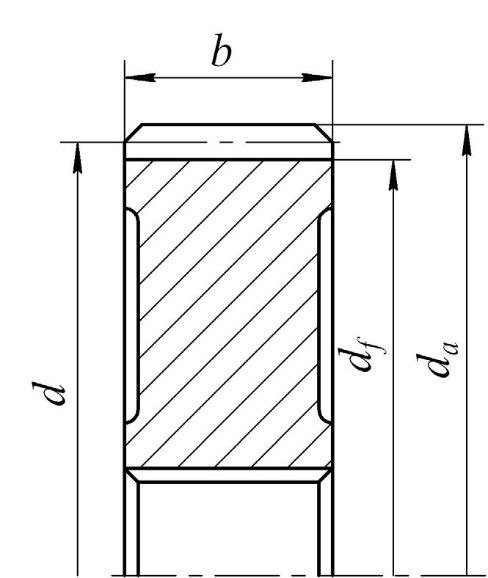
пределяем диаметры вершин зубьев шестерни и зубчатого колеса по формулам
da1 = d1 + 2 ⋅ m и da2 = d2 + 2 ⋅ m
da1 = 98,25 + 2 ⋅ 5 = 108,25 мм
da2 = 301,75 + 2 ⋅ 5 = 311,75 мм
Рис. 2 Геометрические
параметры зубчатого колеса
Находим диаметры впадин зубьев шестерни и зубчатого колеса по формулам
d f 1 = d1 − 2,5 ⋅ m и d f 2 = d2 − 2,5 ⋅ m
d f 1 = 98,25 − 2,5 ⋅ 5 = 85,75 мм d f 2 = 301,75 − 2,5 ⋅ 5 = 289,25 мм
Определяем ширину шестерни b1 = b2 + (5...10) мм.
b1 = b2 + 10 = 100 +10 = 110 мм
2.5 Расчет сил в зацеплении цилиндрической передачи
Силы, действующие в зацеплении цилиндрической косозубой передачи, показаны на рис. 3. Схема соответствует случаю вращения шестеренки по часовой стрелке.
Окружная сила на шестеренке равна окружной силе на зубчатом колесе
Ft1 = Ft2 = 2 ⋅ T2 ⋅ 103 / d2
Ft1 = Ft2 = 2 ⋅ 916,38 ⋅ 103 / 301,75 = 6074 Н
Радиальная сила на шестеренке равна радиальной силе на зубчатом колесе
Fr1 = Fr2 = Ft1 ⋅ tgα / cosβ Fr1 = Fr2 = 6074 ⋅ 0,364 / 0,7125 = 3103 Н
Осевая сила на шестеренке равна осевой силе на зубчатом колесе (только для косозубых цилиндрических передач)
Fa1 = Fa2 = Ft1 ⋅ tgβ Fa1 = Fa2 = 6074 ⋅ 0,3968 = 2410,1 Н
Выбираем смазку для цилиндрической передачи И-Г-А46.
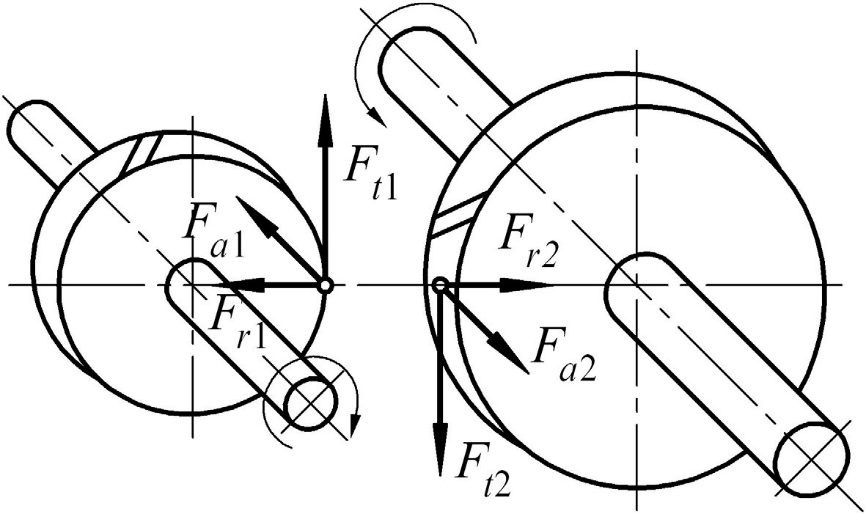
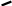
Рис. 3. Силы в цилиндрической передаче
3. Проектирование тихоходного вала
3.1 Расчетная схема вала
KFL1,2 = 6 ,
NFE1,2
где NF lim – базовое число циклов напряжений изгиба NF lim = 4 ⋅ 106;
NFE1,2 – расчетное число циклов напряжений изгиба
Расчетное число циклов напряжений изгиба определяют по формуле
NFE1,2 = KFE ⋅ [60⋅n1,2 ⋅ t] ,
где KFE – коэффициент режима работы при расчете на изгиб
NFE1 = 1 ⋅ (60 ⋅ 645,75 ⋅ 20000) = 774900000
NFE2 = 1 ⋅ (60 ⋅ 205 ⋅ 20000) = 246000000
4 ⋅ 106KFL1 = 6 = 0,42
7749 ⋅ 105
4 ⋅ 106KFL2 = 6 = 0,5
246 ⋅ 106 Так как KFL1,2 < 1, то принимаем KFL1,2 = 1.
2.2 Проектный расчет
Тип передачи: косозубая
Определяем межосевое расстояние по формуле
T2 ⋅ 103 ⋅ KHβ
a′w = Ka (u+1) ⋅ 3 ,
u2 ⋅ѱba ⋅ [σН ]2
где Ka – вспомогательный коэффициент: для косозубых цилиндрических колес Ka = 43 МПа1/3;
ѱba – коэффициент ширины шестерни относительно межосевого расстояния;
KHβ – коэффициент концентрации нагрузки, учитывающий неравномерное распределение нагрузки по линии контакта зубьев. Выбирается в зависимости от
ѱbd = 0,5 ⋅ ѱba ⋅ (u+1)
ѱbd = 0,5 ⋅ 0,5 ⋅ (3,15+1) = 1,03
Рис. 1. Схема цилиндрической зубчатой передачи
916,38 ⋅ 103 ⋅ 1,04
a′w = 43 ⋅ (3,15+1) ⋅ 3 = 163,46 мм
3,152 ⋅ 0,5 ⋅ 5002
Полученное значение a′w округляем до стандартного межосевого расстояния aw по ГОСТ 2185-66 «Передачи зубчатые цилиндрические. Основные параметры»Принимаем aw
= 200 мм
Определяем ширину зубчатого колеса по формуле: b′2 = ѱba ⋅ aw
b′2 = 0,5 ⋅ 200 = 100 мм
Полученное значение b′2 округляем до значения b2 по предпочтительному ряду Ra 40 по ГОСТ 6636-69
Принимаем b2 = 100 мм
Ориентировочно определяем модуль зацепления передачи по формуле
m′ = b2 / ѱm , где ѱm – коэффициент модуля
m′ = 100 / 20 = 5 мм
Полученное значение m′ округляем до стандартного значения m по ГОСТ 9563-80 «Основные нормы взаимозаменяемости. Колеса зубчатые. Модули».
Принимаем m = 5 мм
Назначаем угол наклона зубьев для шевронных колес β = 45°
Задаем направление наклона зубьев: для шестеренки – левое, для зубчатого колеса – правое.
Определяем коэффициент осевого перекрытия по формуле
εβ = (b2 ⋅ sinβ) / (π ⋅ m) ≥ 1,1
εβ = (100 ⋅ sin45°) / (3,14 ⋅ 5) = 4,52
Определяем суммарное число зубьев передачи по формуле
z∑ = 2 ⋅ aw ⋅ cosβ / m
z∑ = 2 ⋅ 200 ⋅ cos45° / 5 = 57
Определяем число зубьев шестерни z1 и колеса z2 с округлением до целого числа по формуле
z1 = z∑ / (u+1) z2 = z∑ - z1
z1 = 57 / (3,15+1) = 14 z2 = 57 – 14 = 43
Уточняем передаточное число u = z2 / z1 u = 43 / 14 = 3,07
Проверка: Δu = (3,07 – 3,15) ⋅ 100 / 3,15 = - 2,5% ≤ ±4% условие выполнено
Уточняем значение угла наклона зубьев с точностью до секунды по формуле
cosβ = [0,5 ⋅ (z1 + z2) ⋅ m] / aw
cosβ = [0,5 ⋅ (14 + 43) ⋅ 5] / 200 = 0,7125
Определяем коэффициент торцевого перекрытия по формуле
εα = [1,88 – 3,2 ⋅ (1 / z1 + 1 / z2)] ⋅ cosβ
εα = [1,88 – 3,2 ⋅ (1 / 14 + 1 / 43)] ⋅ 0,7125 = 1,12 ≥ 1,1
Определяем делительные диаметры шестерни и зубчатого колеса по формулам
d1 = m ⋅ z1 / cosβ и d2 = m ⋅ z2 / cosβ
d1 = 5 ⋅ 14 / 0,7125 = 98,25 мм d2 = 5 ⋅ 43 / 0,7125 = 301,75 мм
Определяем окружную скорость по формуле
υ = π ⋅ d1 ⋅ n1 / 60 υ = 3,14 ⋅ 98,25 ⋅ 645,75 / 60 = 3,32 м / с
Назначаем степень точности и вил сопряжения цилиндрической передачи согласно ГОСТ 1643-81 «Основные нормы взаимозаменяемости. Передачи зубчатые цилиндрические. Допуски»
Степень точности: 9-В
2.3 Проверочный расчет
По контактным напряжениям
Определяем контактные напряжения по формуле
σН = ZE ⋅ ZH ⋅ Zε ⋅ 2 ⋅ T2 ⋅ 103 ⋅ (u+1) ⋅ KH ≤ [σН ]
d22 ⋅ b2
где ZE – коэффициент, учитывающий свойства материала шестерни и колеса, ZE =275 МПа1/2;
ZH – коэффициент, учитывающий форму сопряжения поверхностей зубьев;
Zε – коэффициент, учитывающий суммарную длину контактной линии;
KH – коэффициент расчетной нагрузки при расчете на контактные напряжения.
ZH = 2 ⋅ cosβ = 2 ⋅ 0,7125 = 1,38
sin2α sin40°
Для косозубой передачи Zε = 1 = 1 = 0,94
εα 1,12
Коэффициент KH определяется как KH = KHβ ⋅ KHν ⋅ KHα
где KHβ – коэффициент концентрации нагрузки (определен ранее);
KHv – коэффициент динамичности нагрузки, учитывающий дополнительную динамическую нагрузку;
KHα – коэффициент нагрузки в зацеплении, учитывающий неравномерность распределения нагрузки между парами зубьев (только для косозубых передач);
KH = 1,04 ⋅ 1,0432 ⋅ 1,13 = 1,23
σН = 275 ⋅ 1,38 ⋅ 0,94 ⋅ 2 ⋅ 916,38 ⋅ 103 ⋅ (3,15+1) ⋅ 1,23 = 361,7 МПа ≤ [σН ] ≤ 500 МПа301,752 ⋅ 100
Отклонение возникающего контактного напряжения от допускаемого
ΔσН = (σН - [σН ]) ⋅ 100% / σН ΔσН = (361,7 - 500) ⋅ 100% / 500 = - 27,66%
Условие прочности не выполняется, значит изменяем ширину венца колеса по формуле
b*2 = b2
⋅ (σН / [σН ])2
b*2 = 100 ⋅ (361,7 / 500)2 = 53 мм
σН* = 495,85 МПа ΔσН = (495,85 - 500) ⋅ 100% / 500 = - 0,83% ≤ ±5%
условие выполнено
По напряжениям изгиба
Определяем допускаемые напряжения изгиба по формуле
где YF – коэффициент формы зуба, зависящий от эквивалентного числа зубьев шестерни и колеса: zV1 = z1 / cos3 β и zV 2 = z2 / cos3 β
zV1 = 14 / 0,71253 = 39 YF1 = 3,71
zV2 = 43 / 0,71253 = 119 YF2 = 3,60
[σF ]1 / YF1 = 267,43 / 3,71 = 72,08 [σF ]2 / YF2 = 226,29 / 3,60 = 62,86
Принимаем YF = 3,60
Yβ – коэффициент повышения изгибной прочности зуба косозубых колес (только для косозубых передач), Yβ =1− εβ ⋅(β / 120);
Yβ =1− 4,52 ⋅ (44,36 / 120) = 0,67
Yε – коэффициент распределения нагрузки между зубьями (только для косозубых передач), Yε =1 / εα ;
Yε =1 / 1,12 = 0,89
KF – коэффициент расчетной нагрузки для напряжений изгиба.
Коэффициент KF определяется как KF = KFβ ⋅KFv ⋅KFα,
где KFβ – коэффициент концентрации нагрузки;
KFv– коэффициент динамичности нагрузки;KFα – коэффициент нагрузки в зацеплении (только для косозубых передач)
KF = 1,09 ⋅1,1162⋅1,35 = 1,64
σF = 3,60 ⋅ 0,67 ⋅ 0,89 ⋅ (2 ⋅ 916.38 ⋅ 103 ⋅ 1,64) / (301,75 ⋅ 100 ⋅ 5) = 42,77 МПа ≤ [σF ]2 ≤ 226,29 МПа
2.4 Расчет геометрических параметров цилиндрической передачи
О
пределяем диаметры вершин зубьев шестерни и зубчатого колеса по формуламda1 = d1 + 2 ⋅ m и da2 = d2 + 2 ⋅ m
da1 = 98,25 + 2 ⋅ 5 = 108,25 мм
da2 = 301,75 + 2 ⋅ 5 = 311,75 мм
Рис. 2 Геометрические
параметры зубчатого колеса
Находим диаметры впадин зубьев шестерни и зубчатого колеса по формулам
d f 1 = d1 − 2,5 ⋅ m и d f 2 = d2 − 2,5 ⋅ m
d f 1 = 98,25 − 2,5 ⋅ 5 = 85,75 мм d f 2 = 301,75 − 2,5 ⋅ 5 = 289,25 мм
Определяем ширину шестерни b1 = b2 + (5...10) мм.
b1 = b2 + 10 = 100 +10 = 110 мм
2.5 Расчет сил в зацеплении цилиндрической передачи
Силы, действующие в зацеплении цилиндрической косозубой передачи, показаны на рис. 3. Схема соответствует случаю вращения шестеренки по часовой стрелке.
Окружная сила на шестеренке равна окружной силе на зубчатом колесе
Ft1 = Ft2 = 2 ⋅ T2 ⋅ 103 / d2
Ft1 = Ft2 = 2 ⋅ 916,38 ⋅ 103 / 301,75 = 6074 НРадиальная сила на шестеренке равна радиальной силе на зубчатом колесе
Fr1 = Fr2 = Ft1 ⋅ tgα / cosβ Fr1 = Fr2 = 6074 ⋅ 0,364 / 0,7125 = 3103 Н
Осевая сила на шестеренке равна осевой силе на зубчатом колесе (только для косозубых цилиндрических передач)
Fa1 = Fa2 = Ft1 ⋅ tgβ Fa1 = Fa2 = 6074 ⋅ 0,3968 = 2410,1 Н
Выбираем смазку для цилиндрической передачи И-Г-А46.
Рис. 3. Силы в цилиндрической передаче
3. Проектирование тихоходного вала
3.1 Расчетная схема вала