Файл: Расчетнографическая работа 2 Дисциплина Теоретические основы электротехники.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
НАО «Карагандинский Технический Университет имени Абылкаса Сагинова»
Кафедра: Энергетические
системы
Расчетно-графическая работа №2
Дисциплина: Теоретические основы электротехники
Выполнил: студент группы
ЭЭ – 21 - 4
Шабденов Алексей
Проверил: Ст. преподаватель
Биличенко Е.Н.
2022
Таблица 1 – Исходные данные для выполнения расчётно-графической работы
| Вариант | Рисунок | L1 | L2 | L3 | C1 | C2 | C3 | R1 | R2 | R3 | f | |||
| мГн | мкФ | Ом | Гц | |||||||||||
| 44 | 1,28 | 0,68 | - | 2,73 | 1,62 | - | - | - | 65 | - | 1400 | |||
Таблица 1.1 – Продолжение таблицы 1
| Вариант | e1' | е3' |
| В | ||
| 44 | 141 sin(wt-180°) | 161,4 sin(wt) |
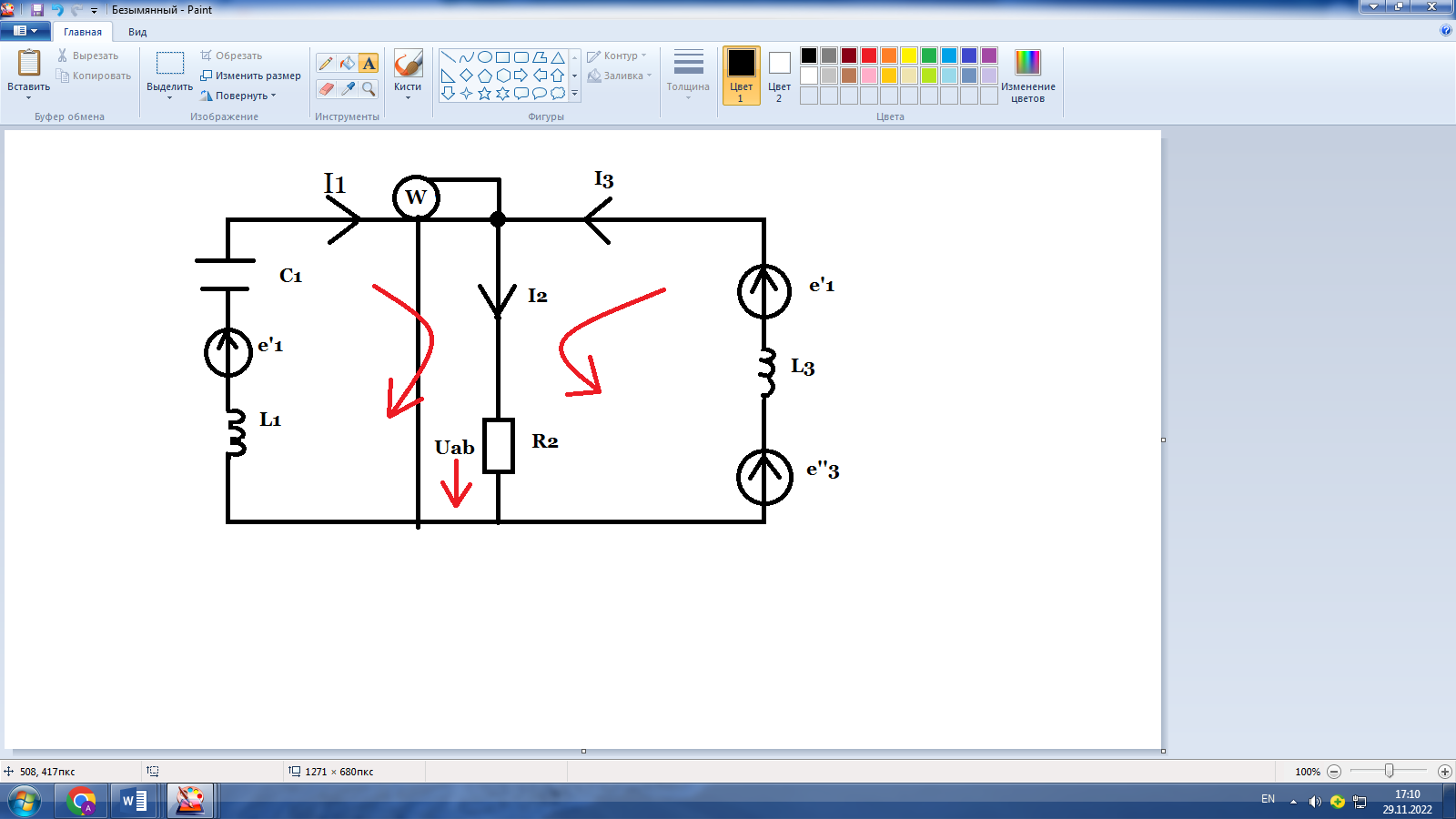
Рисунок 1. Преобразованная схема
Прежде чем приступить к решению мы заранее определим реактивные сопротивления ( конденсатора, катушки), а так же определим угловую частоту.
Угловая частота:
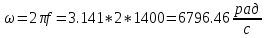
Сопротивления реактивных элементов в схеме:
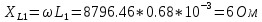
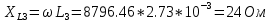
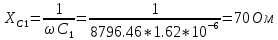
Задание 1. На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав ее в двух формах: а) дифференциальной; б) символической.
а) дифференциальная форма:
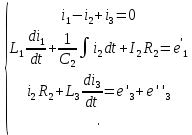
б) символическая форма:
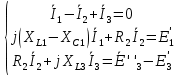
Задание 2. Определить комплексы действующих значений токов во всех ветвях цепи, воспользовавшись одним из методов расчета линейных электрических цепей.
Примечание: все расчёты были выполнены в программе MathCAD 15
В первую очередь необходимо от мгновенных значений ЭДС перейти к комплексам действующих значений ЭДС.
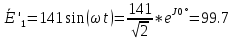 (В)
(В)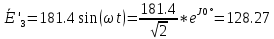 (В)
(В)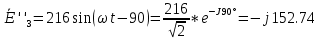 (В)
(В)Комплексные полные сопротивления ветвей:
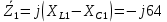 Ом
Ом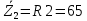 Ом
Ом 
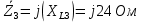
Комплексные проводимости ветвей:
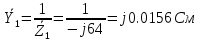
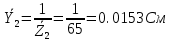
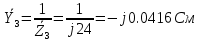
По методу двух узлов расчитаем
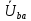 :
: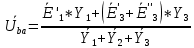
=
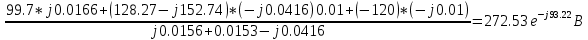
Тогда токи в ветвях:
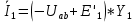
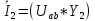
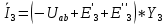
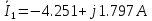
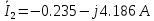
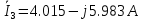
Проверка на основании 1 закона Кирхгофа:
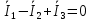
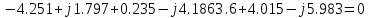
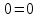
Задание 3. Нахождение показателей ваттметра.
Для того что бы найти показания ваттметра – нужно знать показатели силы тока и напряжения на ветви.
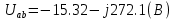
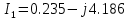 (A)
(A)Определяем значение мощности в комплексном виде:
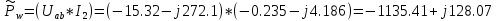 (Вт)
(Вт)Значение ваттметра равно 1135.41 Вт
Задание 4. Построить топографическую диаграмму напряжений, совмещенную с векторной диаграммой токов, приняв равным нулю потенциал точки а.
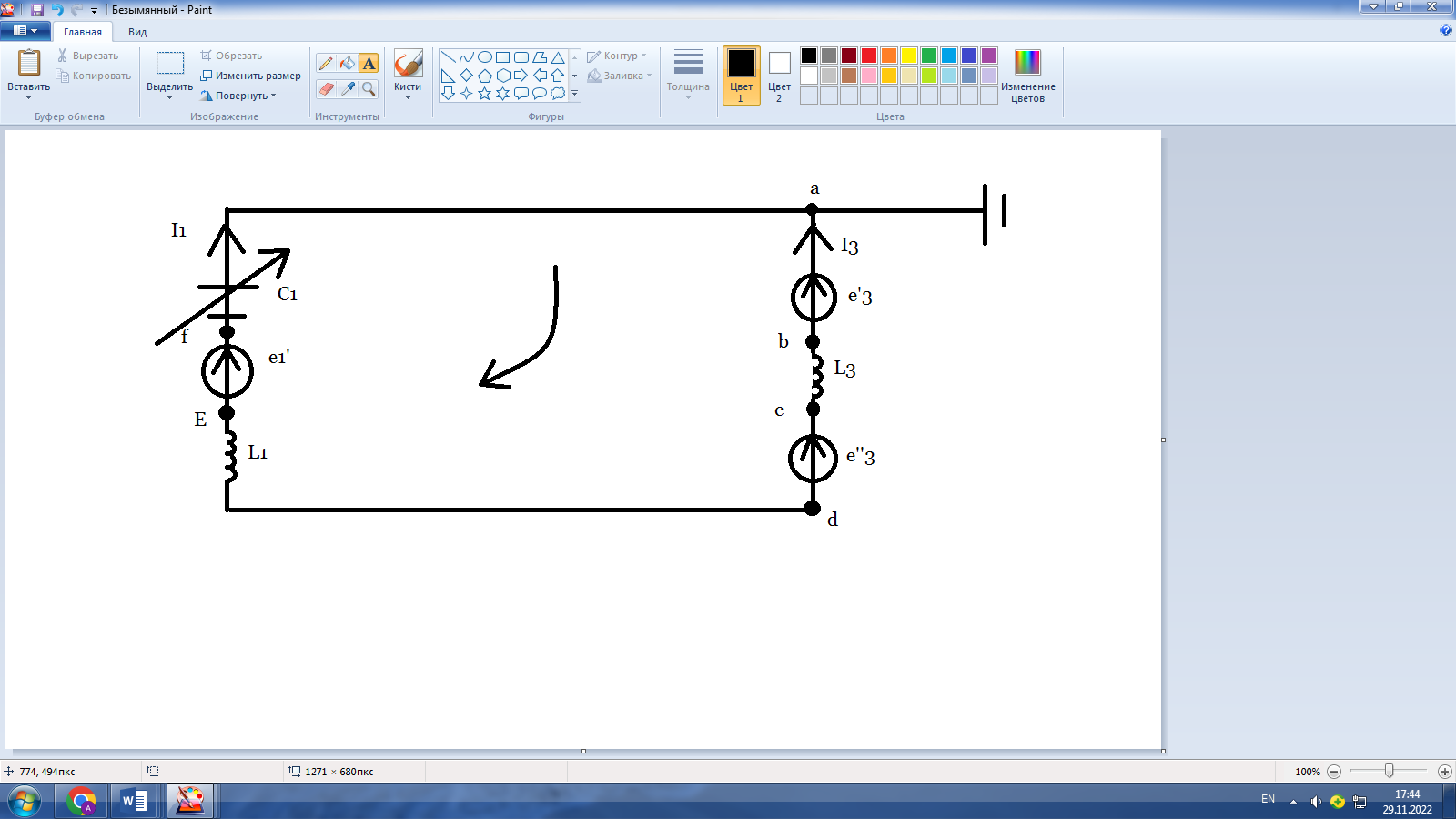
Рисунок 2. Контур для построения топографической диаграммы
Построим топографическую диаграмму для контура, изображенного на рисунке 2. Для этого необходимо найти потенциал в каждой точки стоящей после каждого элемента участка. Заземляем узел а, тем самым прировняв его потенциал к нулю.
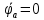
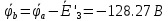
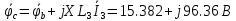
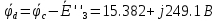
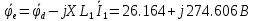
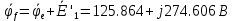
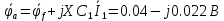
Для построения векторной и топографической диаграммы необходимо на координатной плоскости расположить ось действительных значений (ось абсцисс) и ось мнимых значений (ось ординат). Нужно учитывать, что значения тока и потенциалов сильно различаются, в следствии этого необходимо подобрать масштаб.
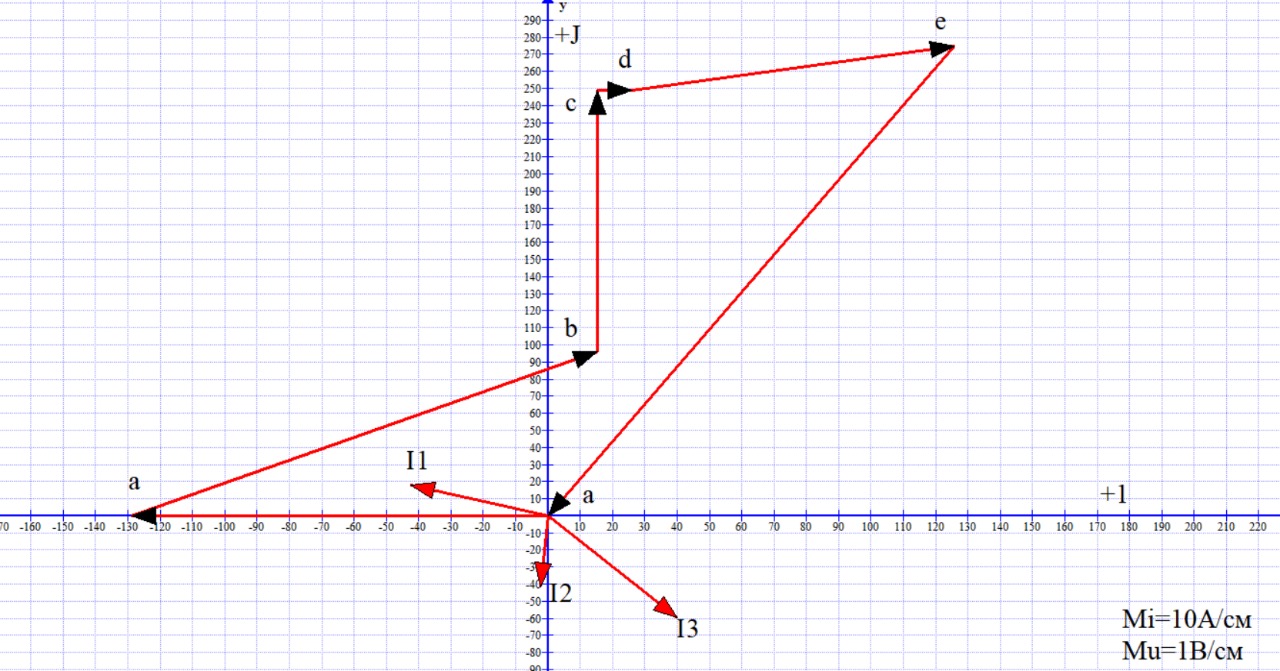
Рисунок 3. Векторная и топографическая диаграмма
Задание 5. Построить круговую диаграмму тока в одном из сопротивлений цепи при изменении модуля этого сопротивления в пределах от нуля до бесконечности. Сопротивление, подлежащее изменению, показано на схеме стрелкой.
Расчет для построения круговой диаграммы ведем по методу эквивалентного генератора.
Разрываем ветвь с изменяющимся сопротивлением ХС1 и определяем напряжение в месте разрыва - напряжение холостого хода Uxx.
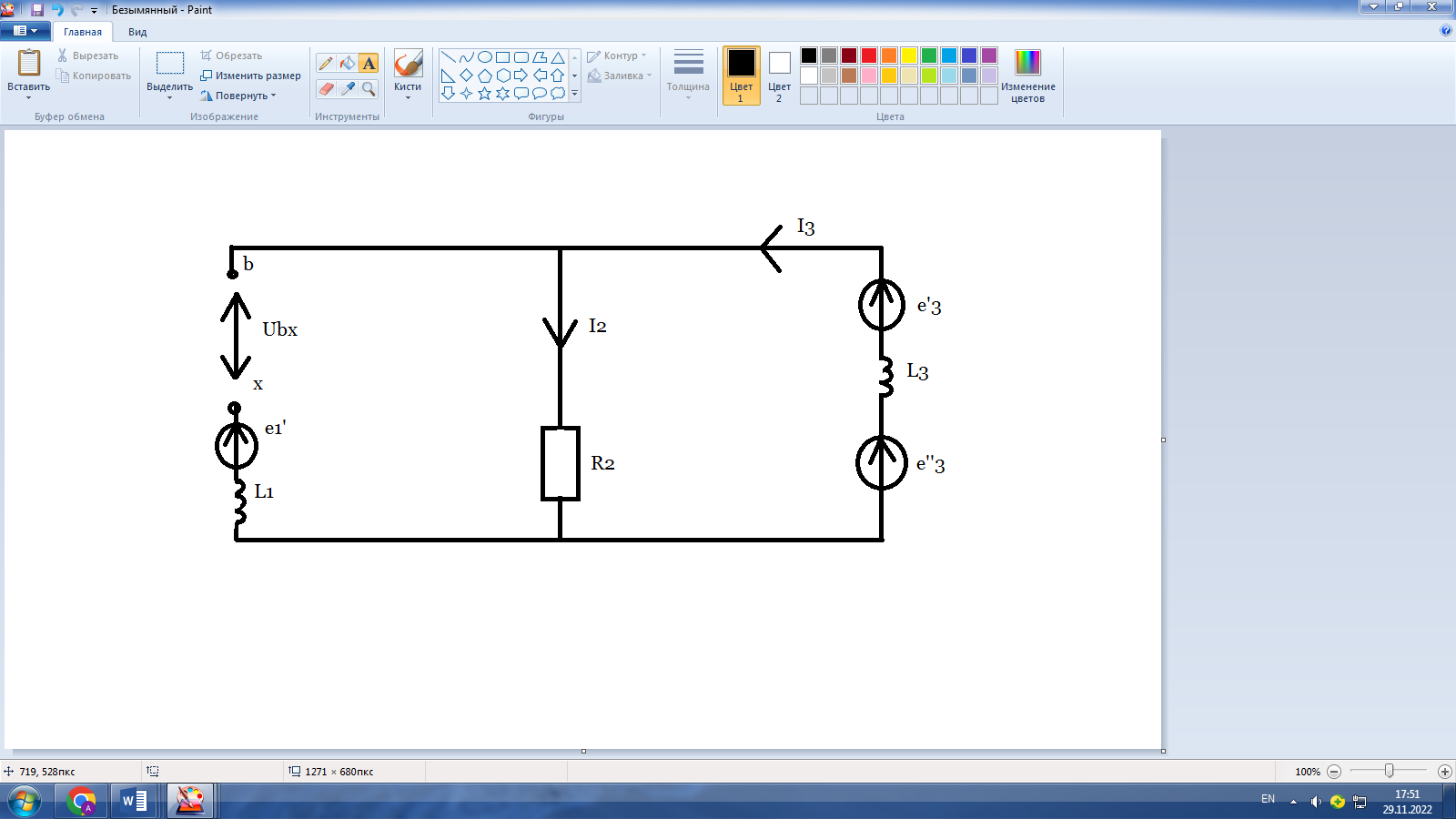
Рисунок 4. Схема с разрывом во второй ветви
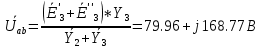
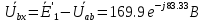
Сопротивление эквивалентного генератора
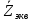 представляет собой сопротивление параллельно включенных комплексных сопротивлений
представляет собой сопротивление параллельно включенных комплексных сопротивлений 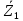 и
и 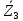 .
.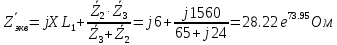
Тогда
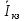 :
: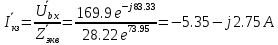
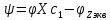 =
= 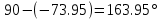
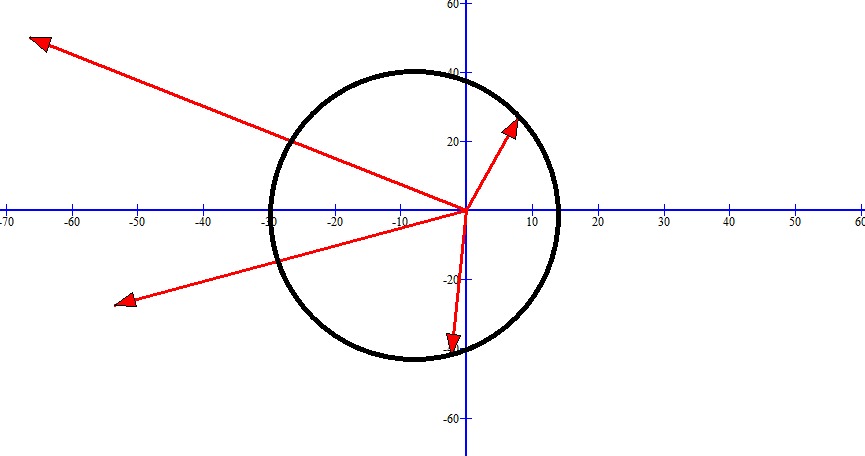
Рисунок 5. Круговая диаграмма токов
Задание 6. Полагая, что между двумя любыми индуктивными катушками, расположенными в разных ветвях заданной схемы, имеется магнитная связь с взаимной индуктивностью М, составить в общем виде систему уравнений по законам Кирхгофа для расчета токов во всех ветвях схемы, записав ее в двух формах: а) дифференциальной, б) символической.
Примечание: поскольку в данной нам схеме отсутствует вторая катушка индуктивности, то и взаимосвязи не будет, однако представим, что в одной из ветвей есть ещё катушка, в таком случае между двумя катушками будет магнитная связь.
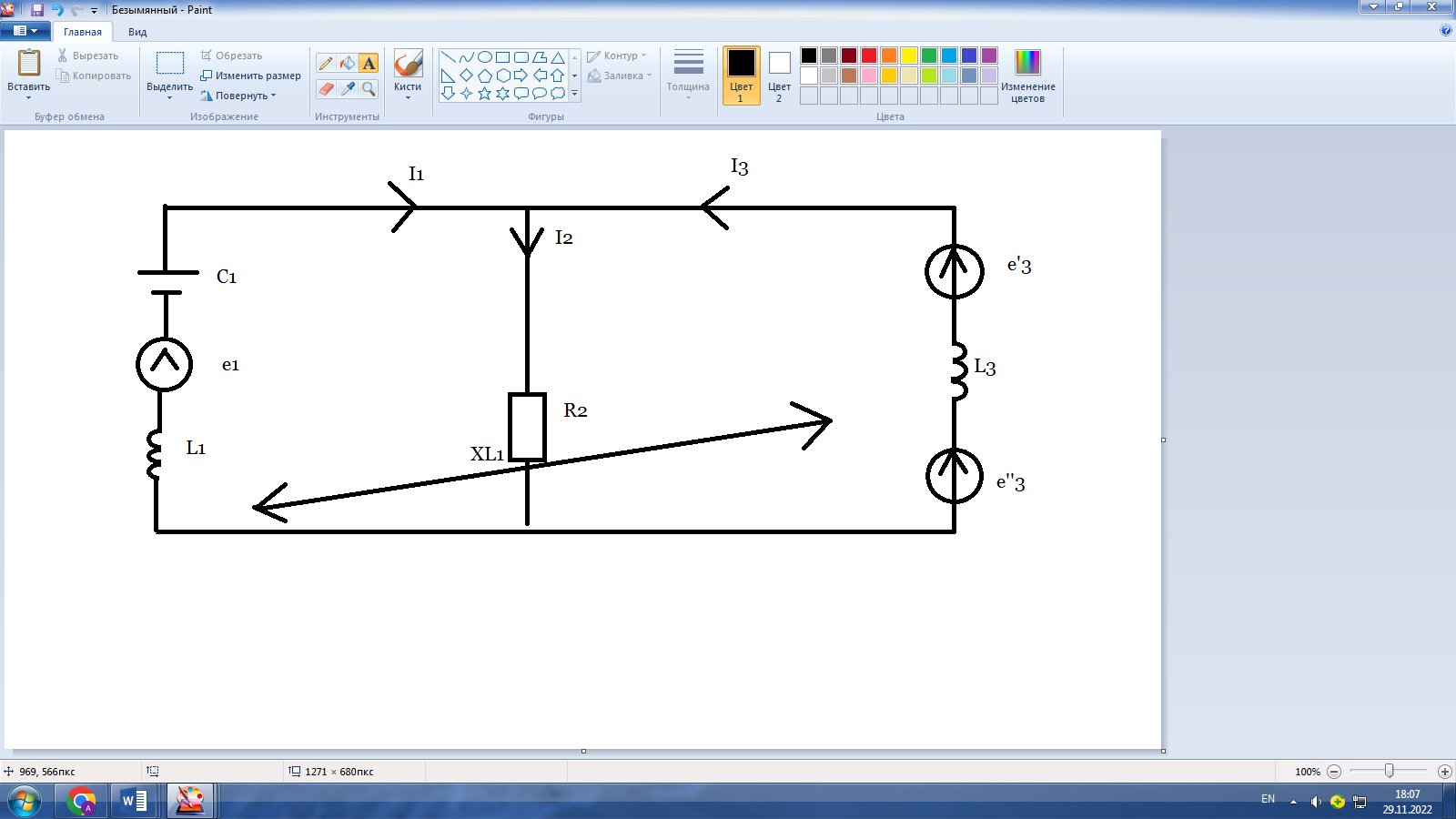
Рисунок 6. Схема с магнитной взаимосвязью
а) дифференциальная форма:
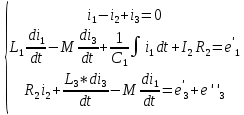
б) символическая форма:
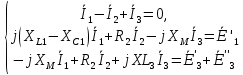
Вывод: во время работы над расчетно- графической работы я научился составлять законы Кирхгофа в символической и дифференциальной формах, так же изучил метод двух узлов, в дополнение научился составлять векторные и круговые диаграммы, выявил влияние взаимной индуктивности на второй закон Кирхгофа