Файл: В математике для решения задач используются определенные.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Введение. Человек в повседневной жизни испытывает необходимость следовать некоторым правилам и указания. К примеру, переходя через дорогу следует нужно выполнить некоторую последовательность действий , убедиться в безопасности выполняемого маневра ,удостовериться что сейчас можно спокойно перейти на другую сторону проезжей части или ее середины. На середине дороги нужно снова посмотреть по сторонам , если машин нет закончить переход. Если же едут машины , то следует дождаться пока они не проедут и только потом идти ( в случает с нерегулируемым пешеходным переходом).Хотя в такой ситуации и автомобиль должен уступить дорогу вступившему на переход пешеходу. Ведь и для водителей есть определенные правила поведения на дороге.
В математике для решения задач используются определенные
правила, описывающие последовательности действий. Часто инструкции и правила представляют собой определенную последовательность действий. Для решения задачи надо знать исходные данные, предполагаемый результат и методы, правила решения и их последовательность. Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, и есть алгоритм.
Применение компьютерных технологий в различных сферах современного общества станет значительно эффективнее, если пользователи овладеют системным подходом в решении прикладных задач, будут иметь представление о методах разработки алгоритмов и составления программ, а
значит - о компьютеризации различных видов деятельности.
Процессор электронно-вычислительной машины, это сложнейшее техническое устройство, умеет выполнять лишь простейшие команды.
Для решения этих задач программист должен составить подробное описание последовательности действий, которые необходимо выполнить центральному процессору компьютера. Составление такого пошагового описания процесса решения задачи называется алгоритмизацией.
1.Алгоритм, определение, свойства, правила построения
1.1 Алгоритм – четкое описание последовательности действий, которые необходимо выполнить для получения результата из исходных данных.
Слово «Алгоритм» происходит от algorithmi – латинского написания имени аль-Хорезми, под которым в средневековой Европе знали величайшего математика из Хорезма (город в современном Узбекистане) Мухаммеда бен Мусу, жившего в 783-850 гг. В своей книге «Об индийском счете» он сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком.
Алгоритм может быть предназначен для выполнения его человеком или машиной. Создание алгоритма, пусть даже самого простого, - процесс творческий. Долгое время считалось, что он доступен только человеку.
Другое дело – реализация уже имеющегося алгоритма. Ее можно поручить
«устройству», которое не обязано вникать в суть дела. Такое «устройство» принято считать формальным исполнителем.
Примером формального исполнителя может служить стиральная машина-автомат, неукоснительно исполняющая заданные ей команды, даже
если вы забыли положить в нее стиральный порошок. Человек тоже может выступать в роли формального исполнителя (например, военнослужащий,
охраняющий склад боеприпасов и действующий согласно алгоритмам,
записанным в устав караульной службы), но в первую очередь формальными исполнителями являются различные автоматические устройства, и компьютер в том числе.
Каждый алгоритм создается для вполне конкретного исполнителя. Те действия, которые может совершать исполнитель, называются его допустимыми действиями. Совокупность допустимых действий образует систему команд исполнителя. Алгоритм должен содержать только те действия, которые допустимы для данного исполнителя.
1.2 Данное определение алгоритма нельзя считать строгим - не вполне ясно, что такое «четкое описание» или «последовательность действий, необходимая для получения результата». Для этого формулируют несколько общих свойств алгоритмов, позволяющих отличать алгоритмы от других инструкций.
Такими свойствами являются:
Дискретность (прерывность, раздельность) - алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.
Наличие входных данных. Алгоритм имеет некоторое число входных величин, заданных ему до начала работы. Иногда это число может равняться
нулю, однако это означает, что входные величины должны быть описаны как
часть алгоритма. Даже если входные величины отсутствуют, то какие-то
величины будут описаны в самом алгоритме. В противном случае алгоритм не может быть выполнен.
Наличие выходных данных. Результатом выполнения любого алгоритма всегда будет обработанная информация, выдаваемая в том или ином виде и, следовательно, алгоритм обязательно имеет одну или несколько выходных величин, являющихся результатом обработки входных данных.
Определенность - каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
Чтобы исключить неоднозначность, разработаны определенные подходы для записи алгоритмов. Один из них - запись алгоритма в виде блок схемы, представляющей собой последовательность специальных пиктограмм, каждая из которых однозначно указывает на выполняемое действие. Другой подход заключается в разработке формально определенных языков, в которых каждое утверждение имеет абсолютно точный смысл. При формулировке алгоритма для его выполнения на компьютере применяются языки программирования.
Результативность (конечность) - алгоритм должен приводить к решению
задачи за конечное число шагов. Это требование происходит из теории вычислений, которая пытается провести грань между правильными и неправильными алгоритмами. Алгоритм считают правильным, если на любом допустимом входе он заканчивает работу и выдает результат, удовлетворяющий требованиям задачи. Неправильный алгоритм для некоторого входа может вовсе не остановиться или дать неправильный результат.
Эффективность алгоритма. Алгоритм, который выполняет действие за меньшее число шагов, признается более эффективным. Это связано с тем, что любая программа, в основе которой лежит алгоритм, должна выполняться вычислительном устройстве. Поэтому большое значение имеет время выполнения программы, на которое влияет количество шагов алгоритма. Кроме того, программа занимает определенный объем в памяти компьютера.
Поэтому количество шагов влияет на еще один показатель эффективности - размер программы.
Массовость - алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
1.3 Алгоритм – искусственная конструкция, которую сооружают для достижения определенных целей. Чтобы алгоритм работал верно, его необходимо строить по определенным правилам.
Первое правило – при построении алгоритма необходимо задать множество объектов с которыми будет работать алгоритм. Формальное (закодированное) представление этих объектов называется данными. Алгоритм приступает к работе с некоторым набором данных, которые называются входными, и в результате выдает данные, которые называются выходными. То есть, алгоритм преобразует входные данные в выходные.
Пока мы не имеем формализованных входных данных, мы не можем построить алгоритм.
Второе правило – для работы алгоритма требуется память. В памяти размещаются входные данные, промежуточные и выходные данные, которые являются результатом работы алгоритма. Память состоит из отдельных ячеек, является дискретной. В теории алгоритмов размеры памяти не ограничиваются, считается, что мы можем предоставить алгоритму любой необходимый объем памяти. Практическая работа с алгоритмами (программирование) начинается именно с выполнения данных правил. В языках программирования распределение памяти осуществляется операторами описания переменных.
Третье правило – дискретность. Алгоритм строится из отдельных шагов (действий, операций, команд). И Это множество шагов, из которых составлен алгоритм, должно быть конечно.
Четвертое правило – детерминированность. После каждого шага необходимо указывать, какой шаг выполняется следующим, либо давать команду остановки.
Пятое правило – сходимость (результативность). Алгоритм должен завершать работу после конечного числа шагов. При этом обязательно необходимо указать, что считать результатом работы алгоритма.
В итоге получается что алгоритм –это неопределяемое понятие теории алгоритмов. Алгоритм каждому набору входных данных ставит в
соответствие набор выходных данных, вычисляет функцию. При решении конкретных вопросов в теории алгоритмов всегда применяется одна из конкретных моделей алгоритма.
2. ВИДЫ АЛГОРИТМОВ
Алгоритм применительно к ЭВМ – точное предписание, набор операций, правил и их комбинации, при помощи которого, начиная с исходных данных, можно решить любую задачу фиксированного типа.
Алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, можно характеризовать следующим образом:
Механические алгоритмы, или иначе детерминированные, жесткие ,например, алгоритм работы двигателя машины и тому подобное.
Механический алгоритм задает определенные действия, обозначая их в единственной и достоверной последовательности, обеспечивая требуемый результат, если выполняются те условия задачи, для которых разработан алгоритм.
Гибкие алгоритмы, например стохастические (вероятностные) и эвристические. Вероятностный алгоритм дает программу решения задачи
несколькими путями или способами, приводящими к достижению результата.
Эвристический алгоритм (от греческого слова “эврика”) – алгоритм, в котором достижение конечного результата программы действий однозначно не определено, так как не обозначена вся последовательность действий исполнителя. К эвристическим алгоритмам относят, к примеру, инструкции. В этих алгоритмах используются универсальные логические процедуры и
способы принятия решений, основанные на аналогиях, ассоциациях и опыте решения похожих задач.
Линейный алгоритм – набор команд , выполняемых последовательно во времени друг за другом.
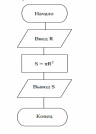
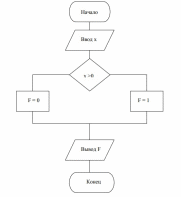
Разветвляющийся алгоритм – алгоритм, содержащий хотя бы одно условие, в результате проверки которого машина обеспечивает переход на один из двух возможных шагов.
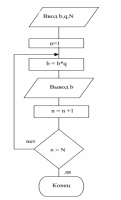
Циклический алгоритм – алгоритм, предусматривающий многократное повторение одного и того же действия над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов. Для примера можно составить алгоритм решения задачи с использованием цикла «ДО», для вычисления N первых членов геометрической прогрессии, используя формулу bn+1 = bn *q для любых b и q, где n текущий член прогрессии.
Вспомогательный алгоритм – алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм.
3 Способы представления алгоритма
Алгоритм является абстракцией и поэтому один и тот же алгоритм можно представить многими способами. Если с алгоритмом работает человек, то он может использовать обычный язык (русский к примеру), язык картинок и пиктограмм, а также математические формулы. В программировании эти проблемы решают путем создания четко определенного набора составных блоков, из которых могут конструироваться представления алгоритмов. Набор правил, устанавливающих, как эти блоков могут комбинироваться для представления более сложных идей, образуют язык программирования.
3.1 Словесное описание алгоритма
Запись действий на естественном языке. Такая форма записи часто приводит к избыточности представления и одновременно к неоднозначности выполнения алгоритма из-за плохой формализации средствами естественных языков. Для лучшей формализации действий используются ограниченный набор ключевых слов, фразы типовой структуры. Словесное описание алгоритма получил значительно меньшее распространение из-за его многословности и отсутствия наглядности.