Файл: В математике для решения задач используются определенные.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Определим форматы переменных A, B, Ф, где A и B — значения для сравнения, Ф — переменная для хранения максимального значения;
получим два значения чисел A и B для сравнения;
сравним A и B.
если A меньше B, значит большее число B.
Поместим в переменную Ф значение B.
Если A не меньше (больше) B, значит большее число A.
Поместим в переменную Ф значение A.
Словесный способ не имеет широкого распространения по следующим причинам:
такие описания строго не формализуемы;
страдают многословностью записей;
допускают неоднозначность толкования отдельных предписаний.
3.2 Графический способ записи алгоритмов
Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.
При графическом способе алгоритм изображается в виде последовательности связанных между собой блоков, каждый из которых соответствует выполнению соответствующих действий. Внутри блока дается описание соответствующего действия.
Данное графическое изображение называется схемой алгоритма или блок-схемой.
Графическое изображение алгоритма часто используется до программирования задачи из-за его наглядности, ибо визуальное восприятие облегчает процесс создания программы, анализ дальнейшего развития проекта и варианты исправления ошибок в ходе тестирования .
Можно встретить даже такое утверждение: “Внешне алгоритм представляет собой схему – набор прямоугольников, других символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации“. Здесь форма представления алгоритма смешивается с самим алгоритмом.
Принцип программирования “сверху вниз” требует, чтобы блок-схема поэтапно раскрывалась и каждый блок “расписывался” до элементарных операций. Данный подход можно применять при решении не самых сложных задач. При решении серьезной задачи блок-схема разрастается до такой степени, что ее невозможно будет просмотреть за один раз.
Блок-схемы удобно использовать для объяснения работы уже существующего алгоритма, при этом в качестве блоков берутся действительные блоки алгоритма, работа которых не нуждается в объяснении. Задача блок-схемы помочь упростить изображение алгоритма, а не усложнить.
Схема - это графическое представление алгоритма, дополненное разъясняющими комментариями. Каждый пункт алгоритма отображается на схеме геометрической фигурой - блоком, различным типам выполняемых действий соответствуют различные геометрические фигуры.
Графические элементы в схеме соединяются линиями, их можно назвать линиями «потока информации». Основное направление идет сверху вниз и слева на право. В других случаях применение стрелок обязательно. По отношению к блоку линии потока могут быть входящими или выходящими. Количество входящих линий для блока ограничений не имеет. Выходящая же линия, напротив, может быть только одна.
Исключение оставляют логические блоки, имеющие не менее двух
выходящих линий потока, каждая из которых соответствует одному из возможных исходов проверки логического условия, а также блоки модификации.
Например, для условия, на основе которого строится ветвление, изображается ромбом. Оператор, в котором происходит обработка информации, изображается прямоугольником.
У любой программы есть начало и конец. На блок-схемах начало и конец программ обозначаются прямоугольниками со скруглёнными углами. Внутри прямоугольников пишут: "Начало", "Конец".
В одной схеме следует использовать блоки одинаковых размеров. Необходимо также нумеровать все блоки. Виды и назначение основных блоков приведены в Таблице 1.
Линии, соединяющие блоки и указывающие последовательность связей между ними, должны проводится параллельно линиям рамки. Стрелка в конце линии может не ставиться, если линия направлена слева направо или сверху вниз. В блок может входить несколько линий, то есть блок может являться преемником любого числа блоков. Из блока (кроме логического) может выходить только одна линия. Логический блок может иметь в качестве продолжения несколько вариантов и из него выходят две линии(п2 таблица1).
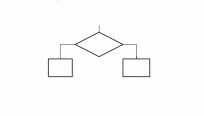
Если на схеме имеет слияние линий, то место их пересечения необходимо выделить точкой. Точку можно не ставить в случае, когда одна линия подходит к другой и слияние их очевидно .
Схему алгоритма нужно выполнять как единое целое, но в случае необходимости можно обрывать , соединяющие блоки линии.
Если при обрыве линии схема находится на этом же листе, то на одном и другом конце линии изображается специальный символ соединитель — окружность диаметром 0,5 мм (п7 таблица1). Внутри парных окружностей указывается один и тот же номер идентификатор. В качестве идентификатора, используется порядковый номер блока, к которому направлен соединитель.

А если схема занимает более одного листа, то в случае разрыва линии используется межстраничный соединитель (п8 таблица1). Внутри каждого такого межстраничного соединителя указывается «адрес» — откуда и куда направлена линия. Адрес записывается в две строки: в первой указывается номер листа, во второй —порядковый номер блока.
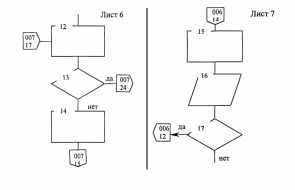
Блок-схема должна содержать все разветвления,
циклы и обращения к подпрограммам, содержащиеся в программе.
Таблица 1. Условные графические обозначения, применяемые при составлении схем алгоритмов.
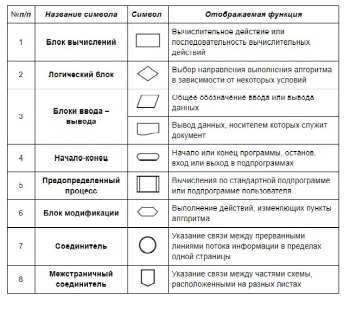
Блок вычислений применяется для обозначения действия, изменяющих значение, размещения данных или форму представления. Для наглядности схемы нескольких блоков обработки можно объединять в один.
Логический блок используется для обозначения переходов управления по условию. В каждом блоке "решение" должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок предопределенный процесс используется для указания обращений к вспомогательным алгоритмам, существующим отдельно в виде самостоятельных модулей и для обращений к подпрограммам.
Блок модификация используется для организации циклических
элементов. Внутри блока записывается параметр цикла, для которого
указываются начальное значение, условия и шаг изменения значения параметра для каждого повторения.
3.3 Псевдокод
Псевдокод - это система обозначений, предназначенная для неформального представления идей в процессе разработки алгоритмов. Он занимает промежуточное место между естественным и формальным языками.
Один из путей создания псевдокода - ослабление правил того формального языка программирования, на котором требуется записать окончательную версию алгоритма. В подобной ситуации псевдокод может состоять из синтаксических и семантических структур, аналогичных структурам целевого языка программирования, но не столь формализованных.
С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи. В псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых однозначно определён. Например, алгоритмы на алгоритмическом языке записываются с помощью служебных слов, представленных в таблице 2
Таблица 2
| алг(алгоритм) | сим (символьный) | дано | да | нет |
| арг(аргумент) | лит (литерный) | надо | для | при |
| рез(результат) | лог(логический) | если | от | до |
| нач(начало) | таб (таблица) | то | знач | выбор |
| кон(конец) | нц(начало цикла) | иначе | и | или |
| цел (целый) | кц (конец цикла) | всё | ввод | вывод |
| вещ (вещественный) | длин(длина) | пока | утв | не |
Вид алгоритма записанный в псевдокоде:
алг название алгоритма (аргументы и результаты)
дано условия применимости алгоритма
надо цель выполнения алгоритма
нач описание промежуточных величин
последовательность команд (тело алгоритма)
кон.
Часть алгоритма от слова алг до слова нач называется заголовком, а часть, заключённая между словами нач и кон — телом алгоритма.