Файл: Цель работы изучить методы цифрового спектрального анализа сигналов, основанные на преобразовании Фурье.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 26
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Цель работы: изучить методы цифрового спектрального анализа сигналов, основанные на преобразовании Фурье.
Вариант – 4
| № варианта | Задание 1 | ||||||
| А1, B | f1, Гц | А2, B | f2, Гц | А3, B | f3, Гц | Sample time | |
| 4 | 30 | 190 | 2 | 195 | 4 | 300 | 1/1000 |
Запустим пакет Simulink и соберем схему, которая суммирует три заданных сигнала и, после прохождения нового сигнала через сглаживающее окно выводила результат на экран.
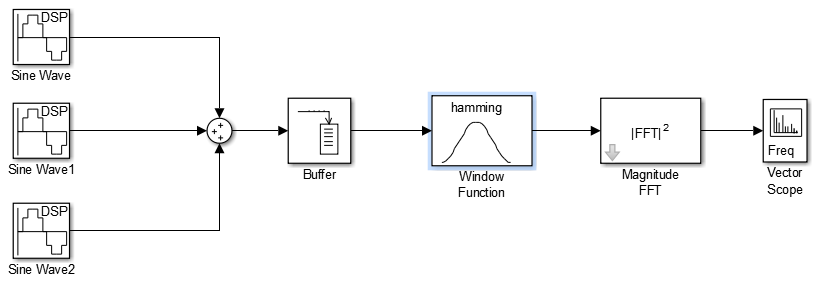
Рисунок 1 – схема для съема результатов задания 1
Настроим блоки Sine Wave заданными параметрами сигналов, блоки Buffer и Magnitude FFT на длительность анализируемого участка установим 1024. Сглаживающее окно будем менять согласно выполняемому заданию.
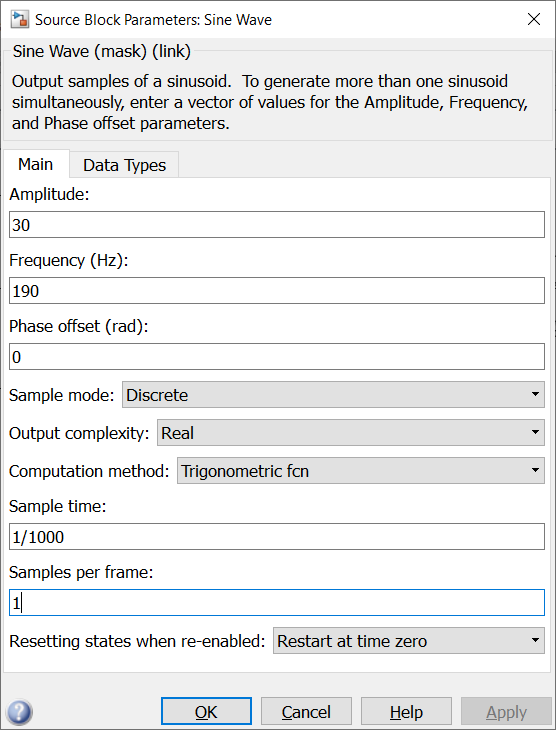
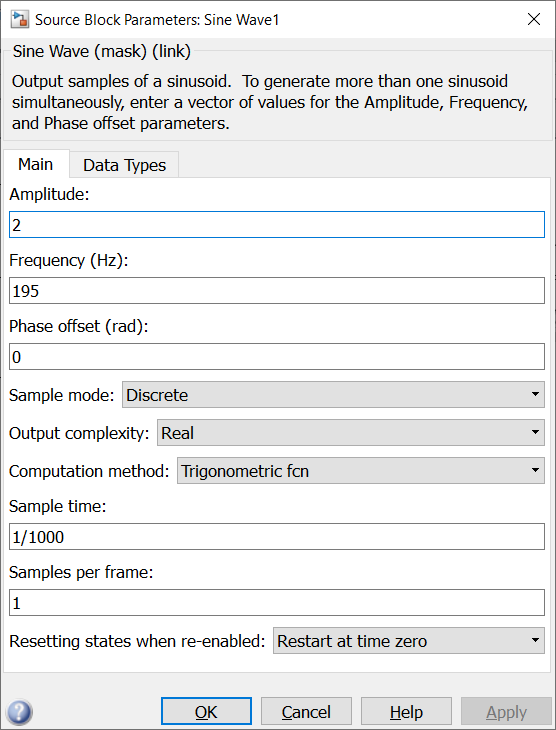
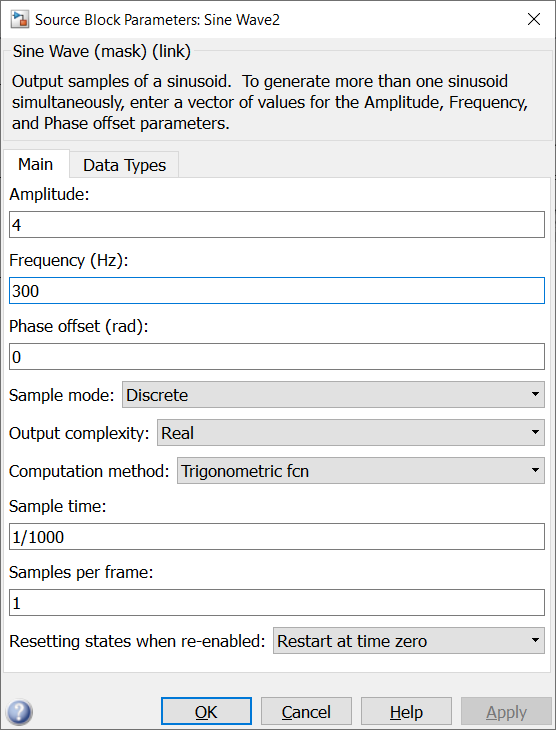
Рисунок 2 – Настройка блоков задающих сигналы
После того как все блоки настроены запустим модель и посмотрим результат.
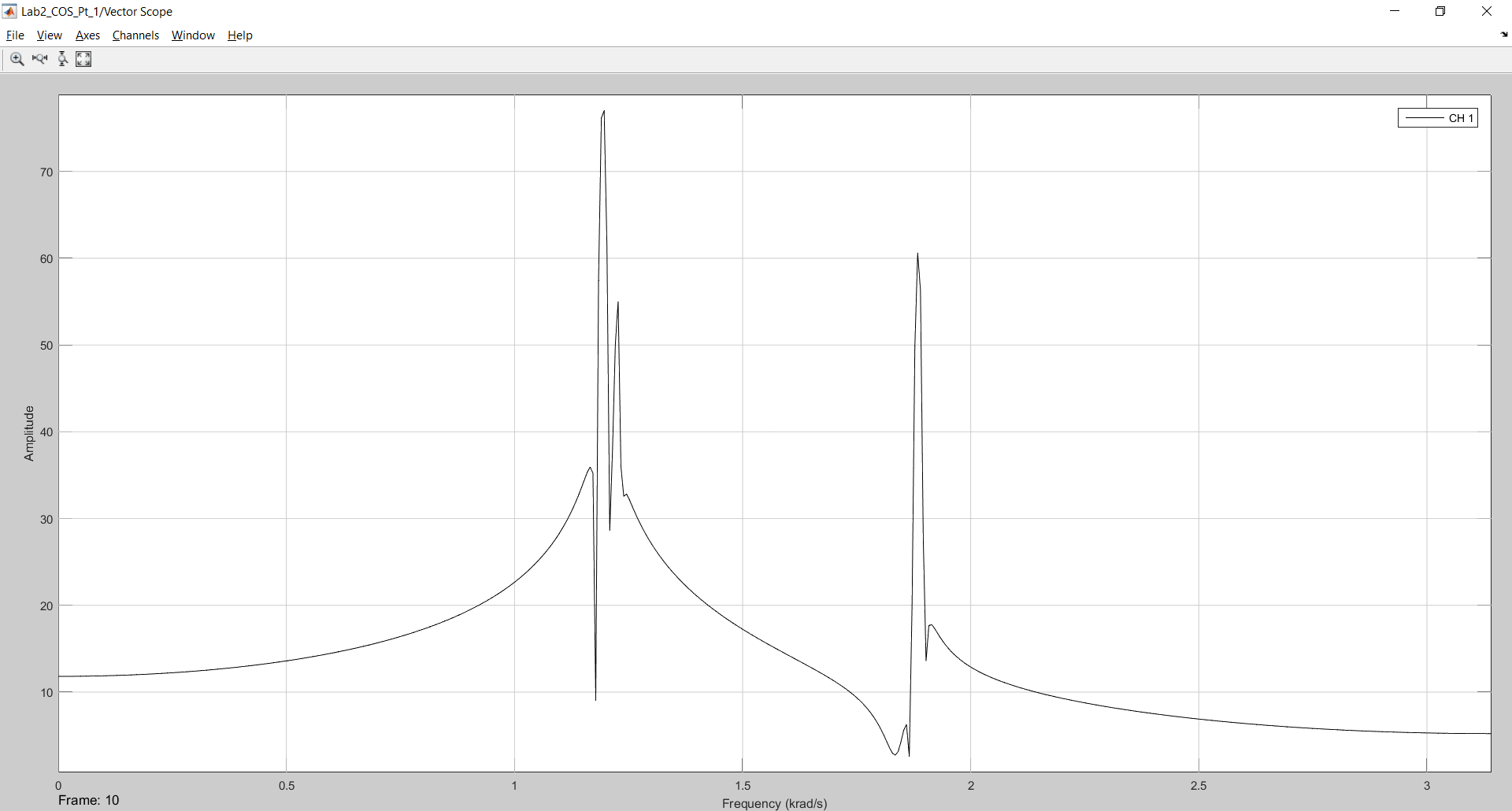
Рисунок 3 - Результат моделирования в 1024 отсчета с использованием сглаживающего окна Хэмминга.
Используя Рисунок 3 определим мощности сигналов в логарифмическом масштабе. Получаем что
P1=77,62 дБ Р2=54,13 дБ Р3=60,07 дБ.
Теперь из децибел переведем в разы с помощью отношения разных мощностей сигналов. Сравним результаты, полученные в ходе моделирования, с теоретическими. Рассчитаем теоретические значения:
, 
, 
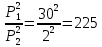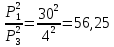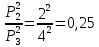.Полученные практические, также переведем в разы.
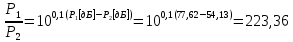
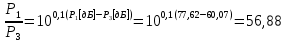
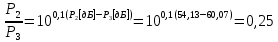
Из полученных практических значений можно заметить, что полученные результаты соотношения близки к теоретическим.
Увеличим размер анализируемого участка до 2048.
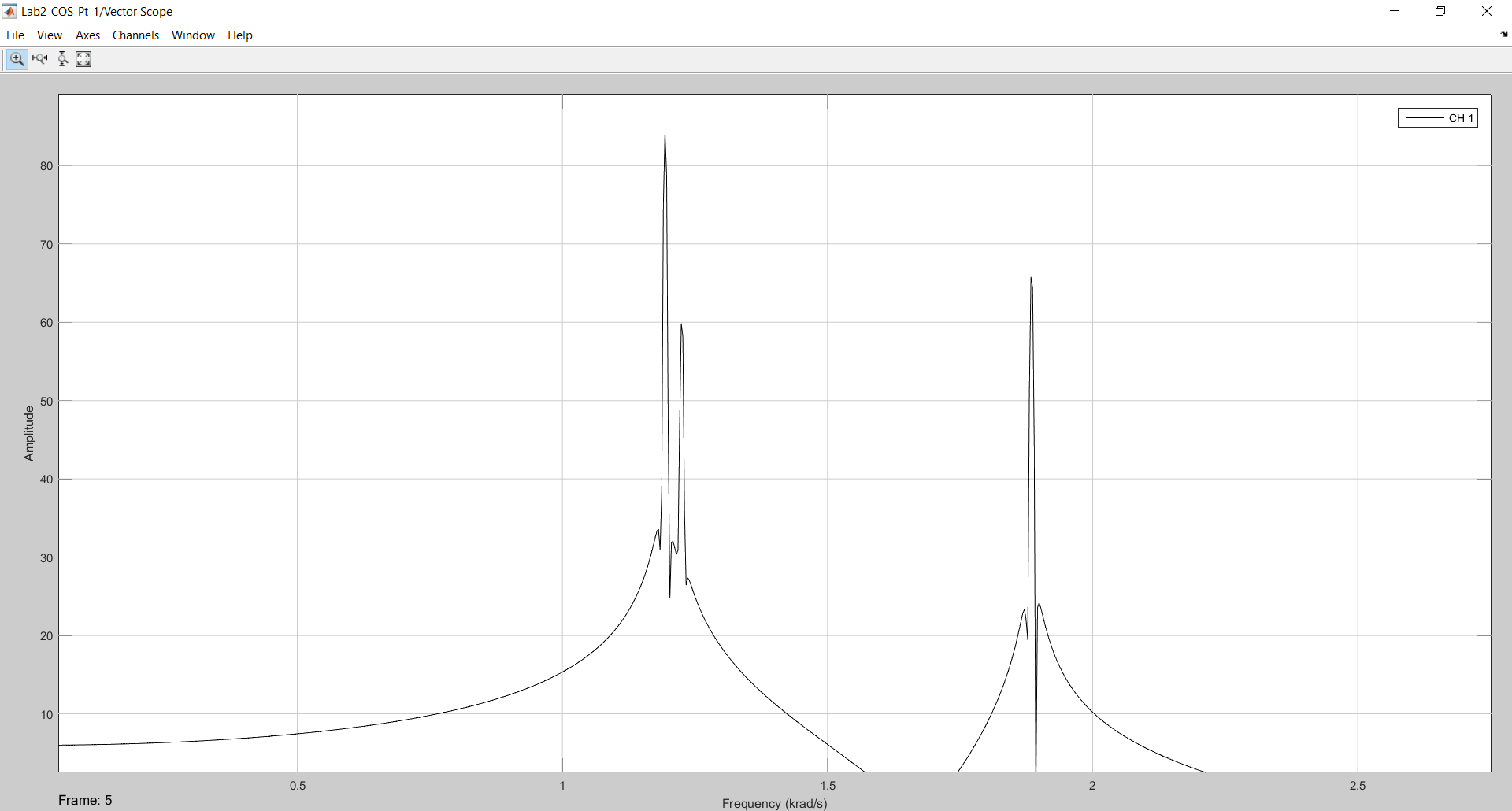
Рисунок 4 - Результат моделирования в 2048 отсчета с использованием сглаживающего окна Хэмминга.
Проведем аналогичные действия по вычислению практических значений и получим:
P1=83,49 дБ Р2=59,98 дБ Р3=65,98 дБ.
, 
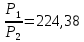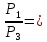56,36, 
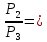0,25. Увеличим еще размер анализируемого участка до 4096.
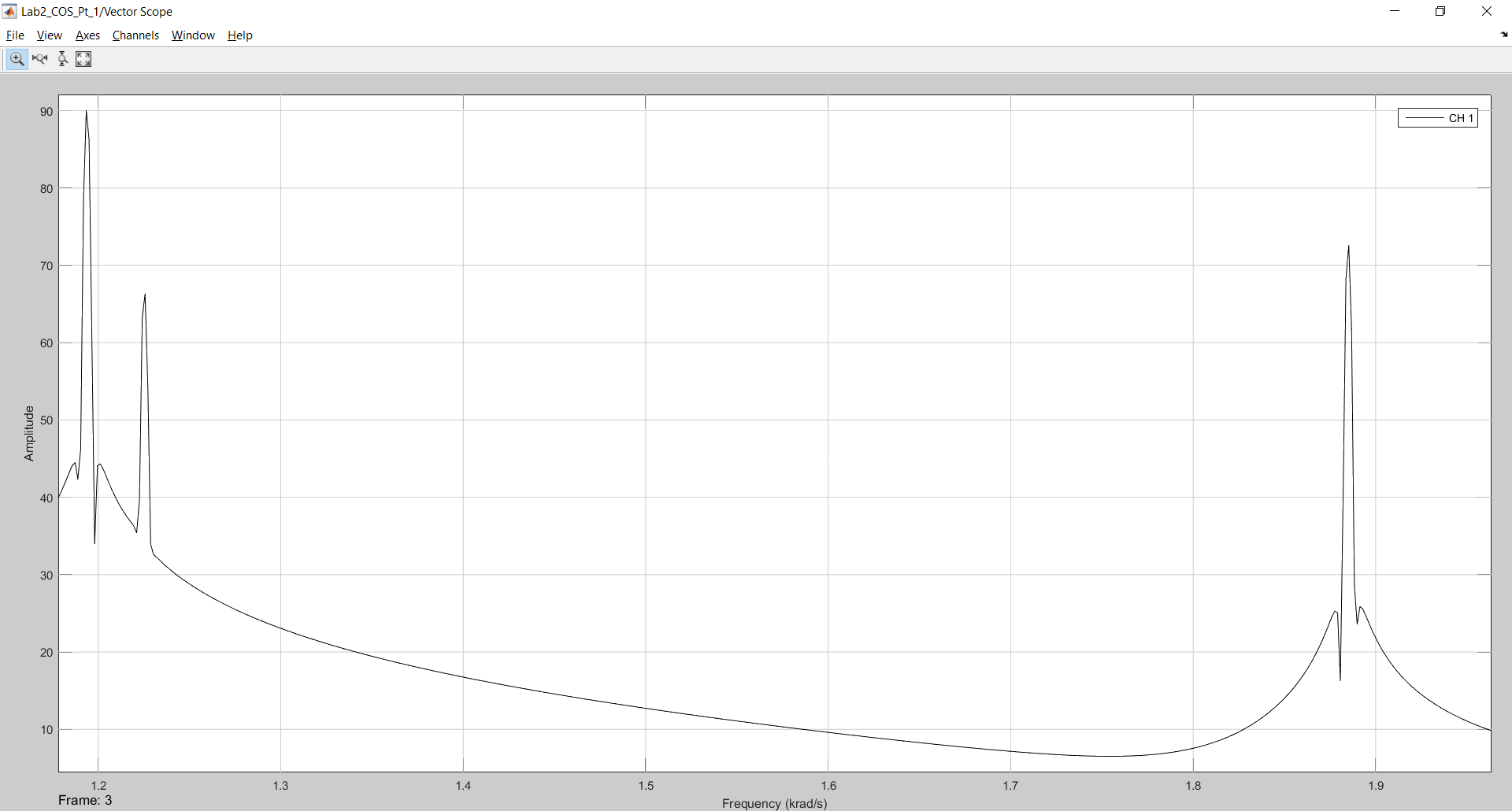
Рисунок 5 - Результат моделирования в 4096 отсчетов с использованием сглаживающего окна Хэмминга.
Здесь получим следующие результаты:
P1=89,98 дБ Р2=66,45 дБ Р3=72,51 дБ.
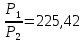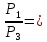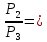, 55,84 0,25.Получили близкие к теоретическим значения.
Увеличивая количество отсчетов анализируемого участка постепенно приближались к более точному значению конечного сигнала который до этого рассчитали, а сам спектр принимал менее искаженную форму.
Восстановим количество отсчетов в значение 2048.Теперь будем анализировать влияние сглаживающих окон на спектр сигнала. Для сглаживающего окна Хэмминга теоретически справедливо определение, что боковые уменьшаются на 40 дБ. Обратимся к рисунку 4. Так как в заданных условиях первый и второй сигналы имеют близкие частоты определить положение боковых сложно, поэтому посмотрим на третий сигнал. Сама несущая имеет мощность Р
3=65,77 дБ, следовательно, боковые должны быть не выше 25 дБ. Из рисунка 4 видно что нижняя боковая находится ниже данного порога, а верхняя немного выше.
Установим окно Ханна. Оно должно уменьшать боковые лепестки на 31,5 дБ. В результате моделирования получим следующий результат.
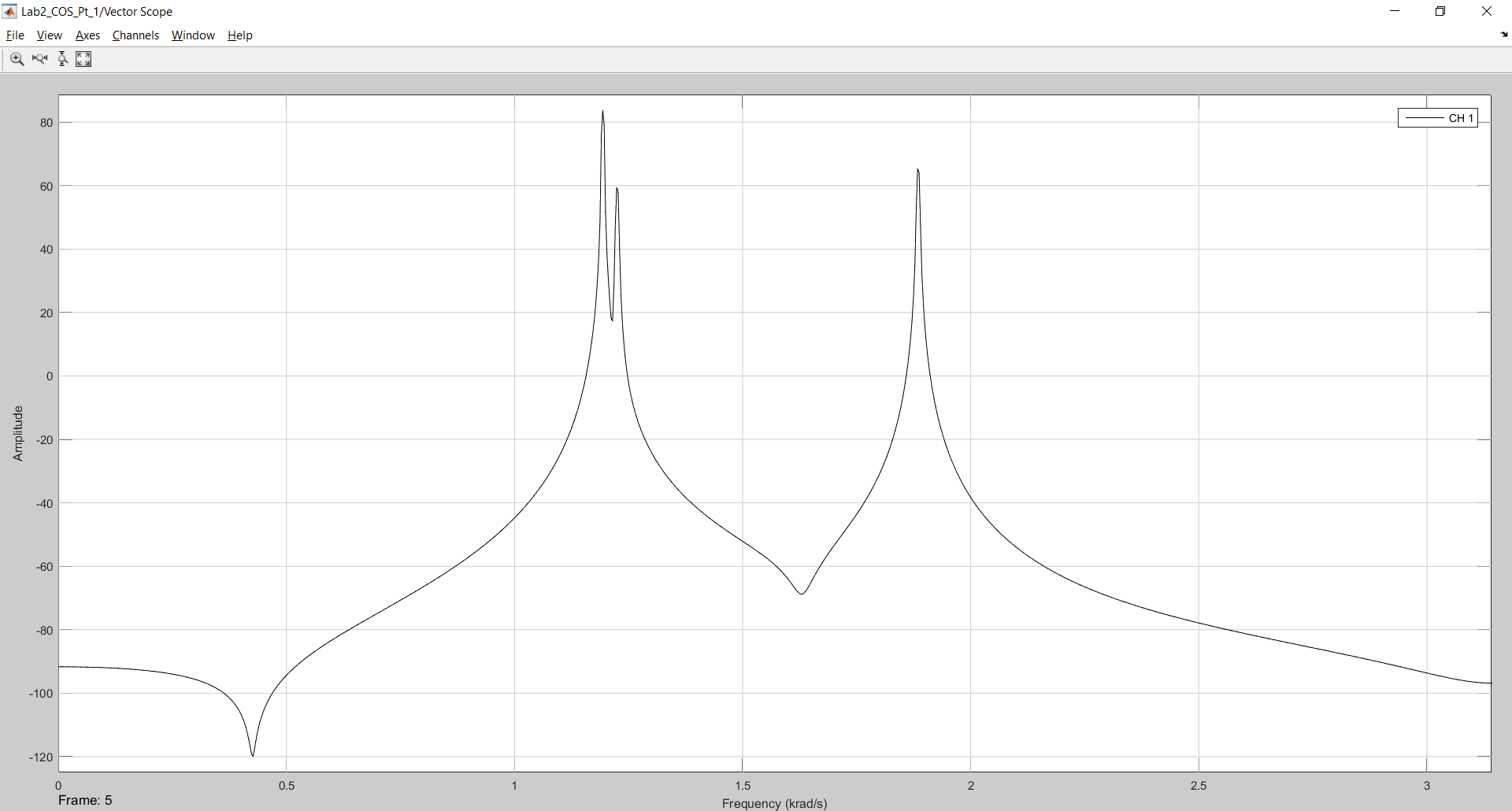
Рисунок 6 - Результат моделирования в 2048 отсчетов с использованием сглаживающего окна Ханна.
Из рисунка 6 получаем, что все боковые лепестки были «сглажены» окном и в результате получили 3 неискаженных сигнала.
Установим окно Блекмэна. Оно должно уменьшать боковые лепестки на 58 дБ. Результат моделирования представлен ниже.
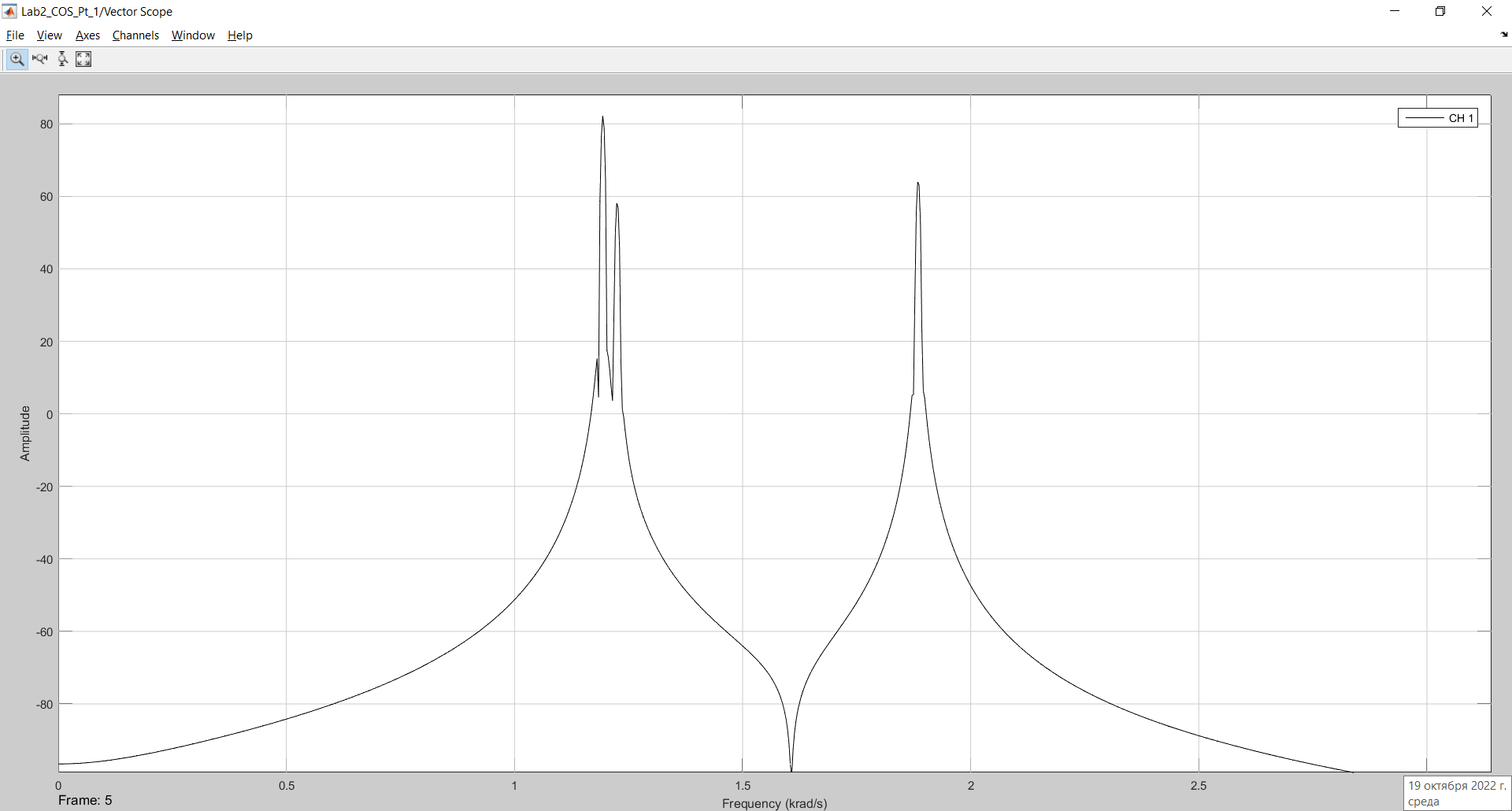
Рисунок 7 – Результат моделирования в 2048 отсчетов с использованием сглаживающего окна Блэкмена.
В отличие от окна Ханна , на рисунке 7 можно увидеть боковые лепестки возле спектра первого сигнала и спектра третьего сигнала и, действительно можно убедиться что находятся они относительно на 58 дБ ниже основного спектра.
Установим окно Кайзера. Оно должно уменьшить боковые лепестки на 32 дБ. Результат моделирования приведен на рисунке 8.
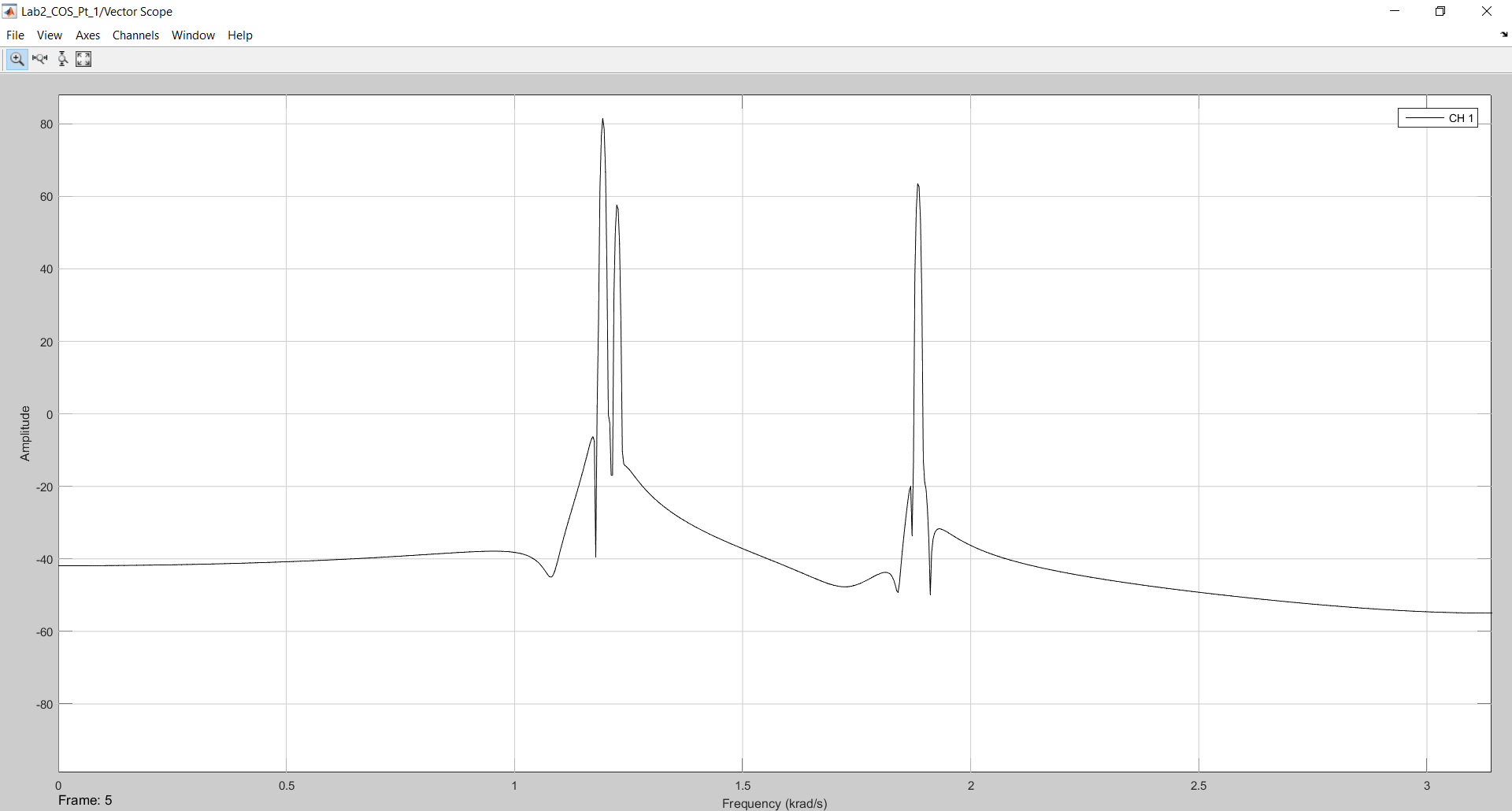
Рисунок 8 – Результат моделирования в 2048 отсчетов с использованием сглаживающего окна Кайзера.
На рисунке 8 можно наблюдать ярко выраженные боковые лепестки. Для сигнала 1 действительно можно сказать, что окно уменьшило боковой лепесток на 32 дБ. Для третьего сигнала действие окна повлияло меньше.
Теперь уберем из схемы сглаживающее окно и посмотрим на результат моделирования.
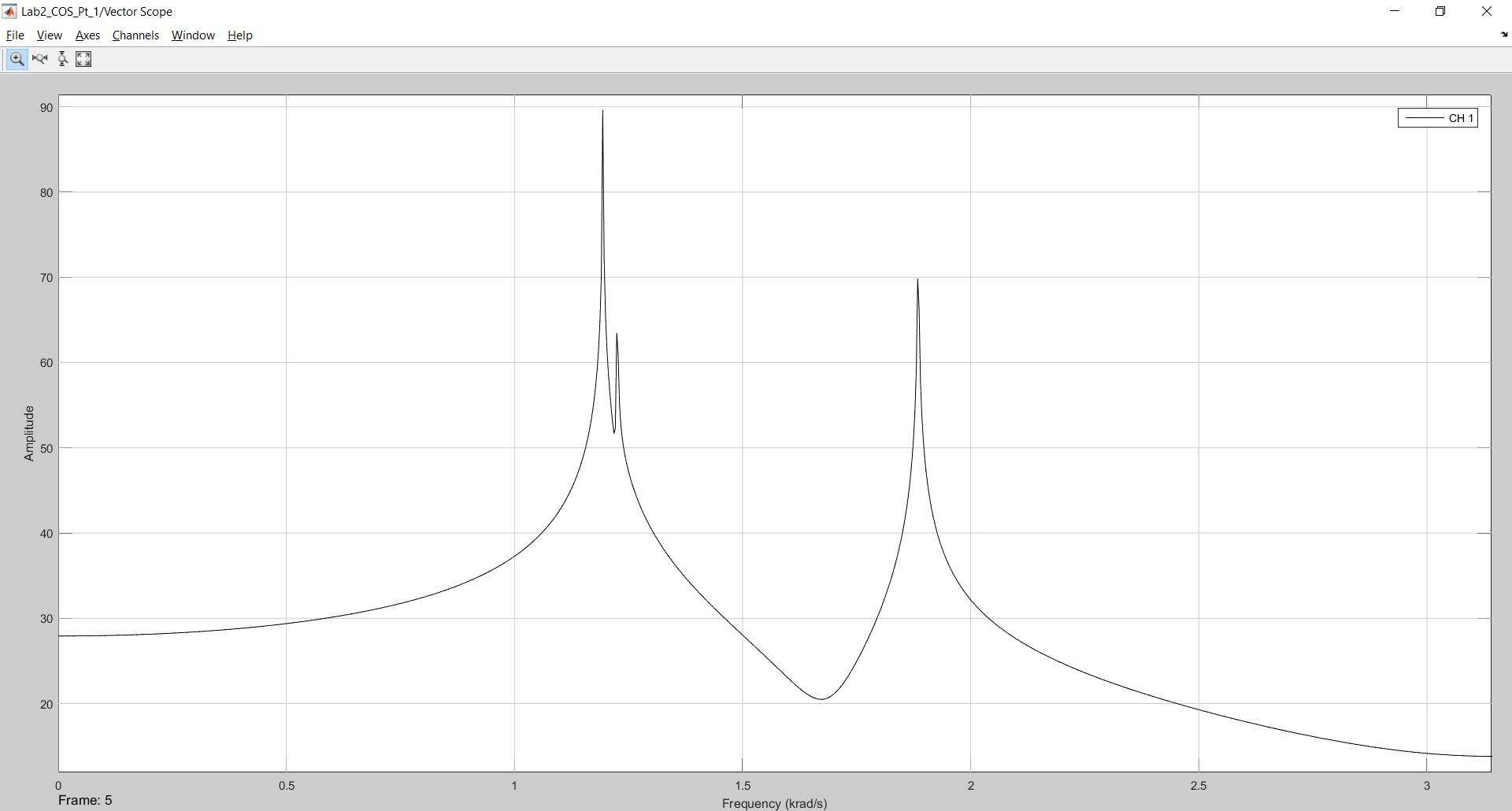
Рисунок 9 - Результат моделирования без сглаживающих окон в 2048 отсчетов.
Добавим в исходную модель источник шума. Мощность шума оставим исходную, а частоту дискретизации настроим как на всех остальных блоках, согласно условию. Получим следующую собранную схему.
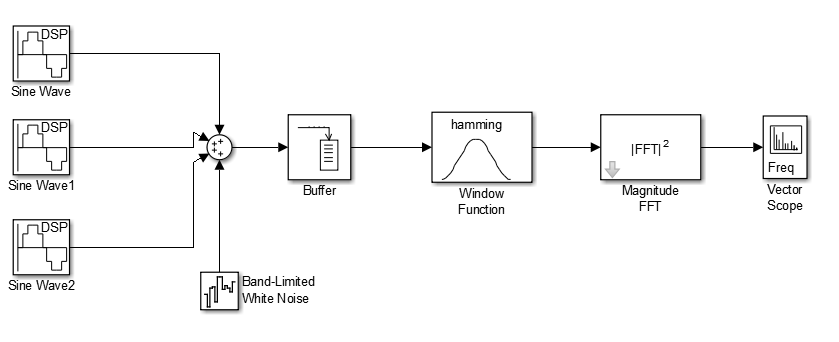
Рисунок 10 – схема с генератором шума.
Запустим модель и посмотрим на результат.
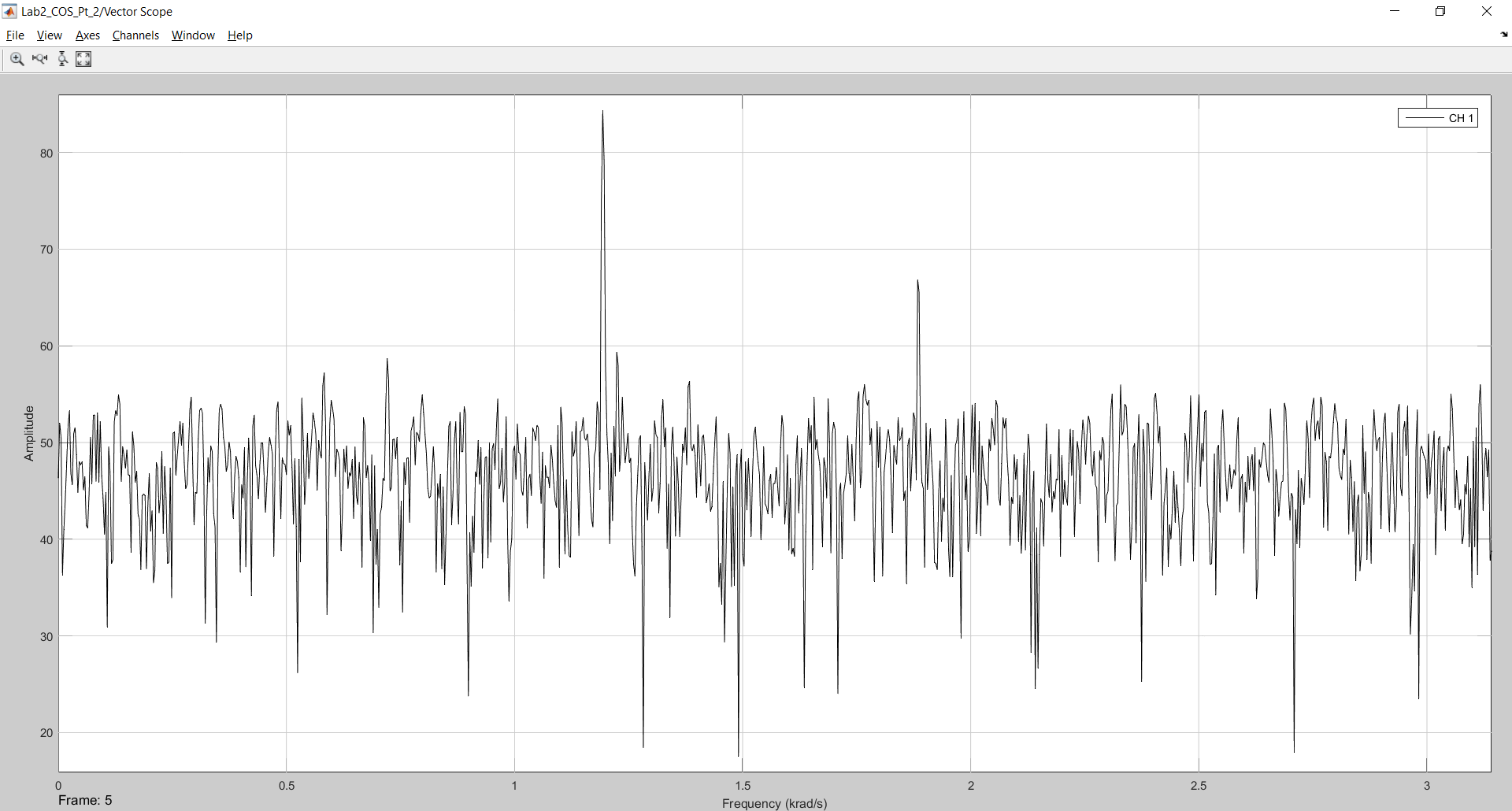
Рисунок 11 – Результат моделирования с генератором шума мощностью 0,1 и количеством отсчетов 2048.
Из рисунка 11 видно, что уже при таком шуме невозможно распознать спектр второго сигнала. Однако еще первый и третий спектры возможно увидеть. Увеличим мощность шума в два раза.
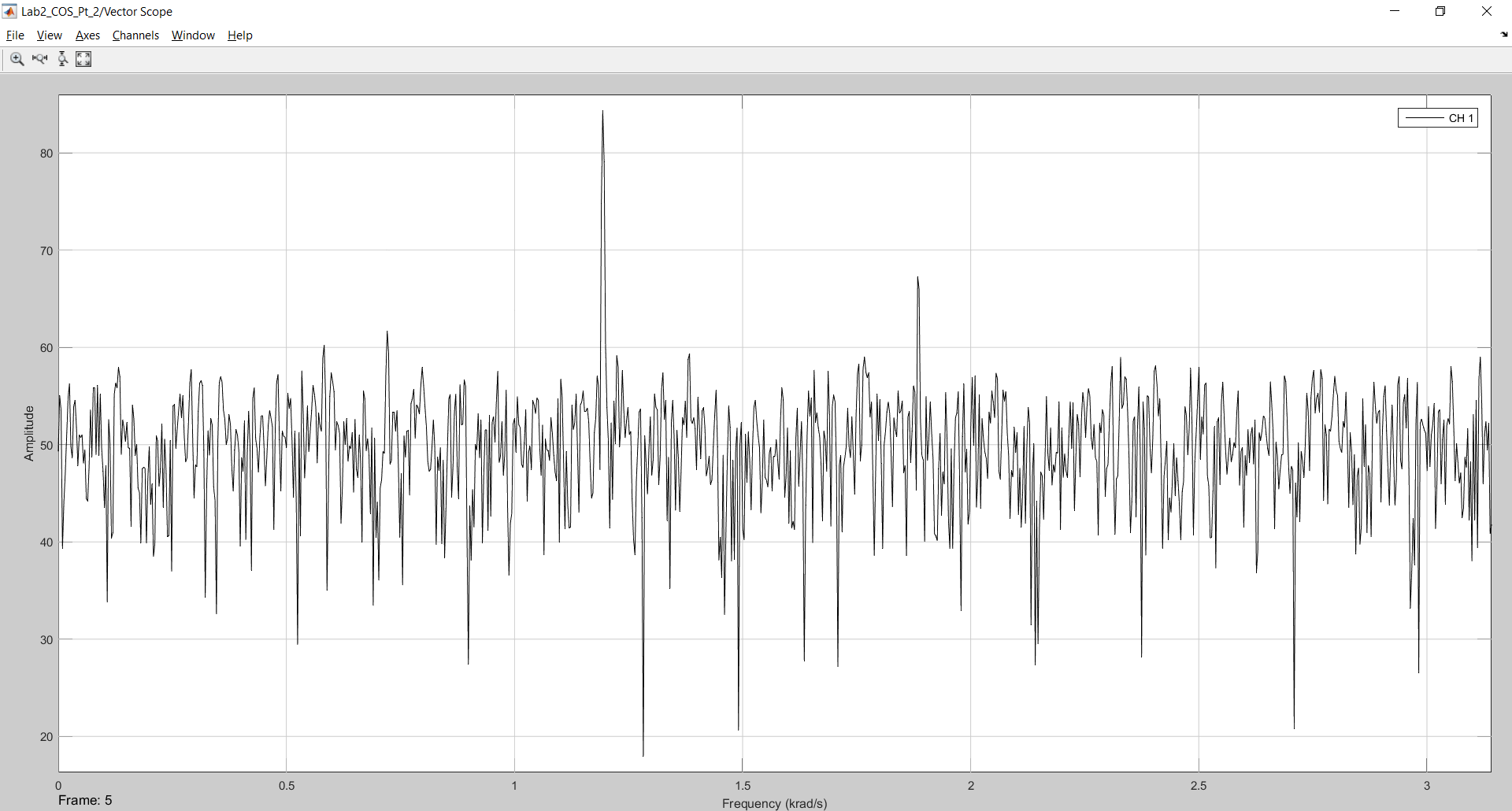
Рисунок 12 – Результат моделирования с генератором шума мощностью 0,2 и количеством отсчетов 2048.
На рисунке 12 еще возможно распознать спектр третьего сигнала. Повысим мощность шума еще в два раза.
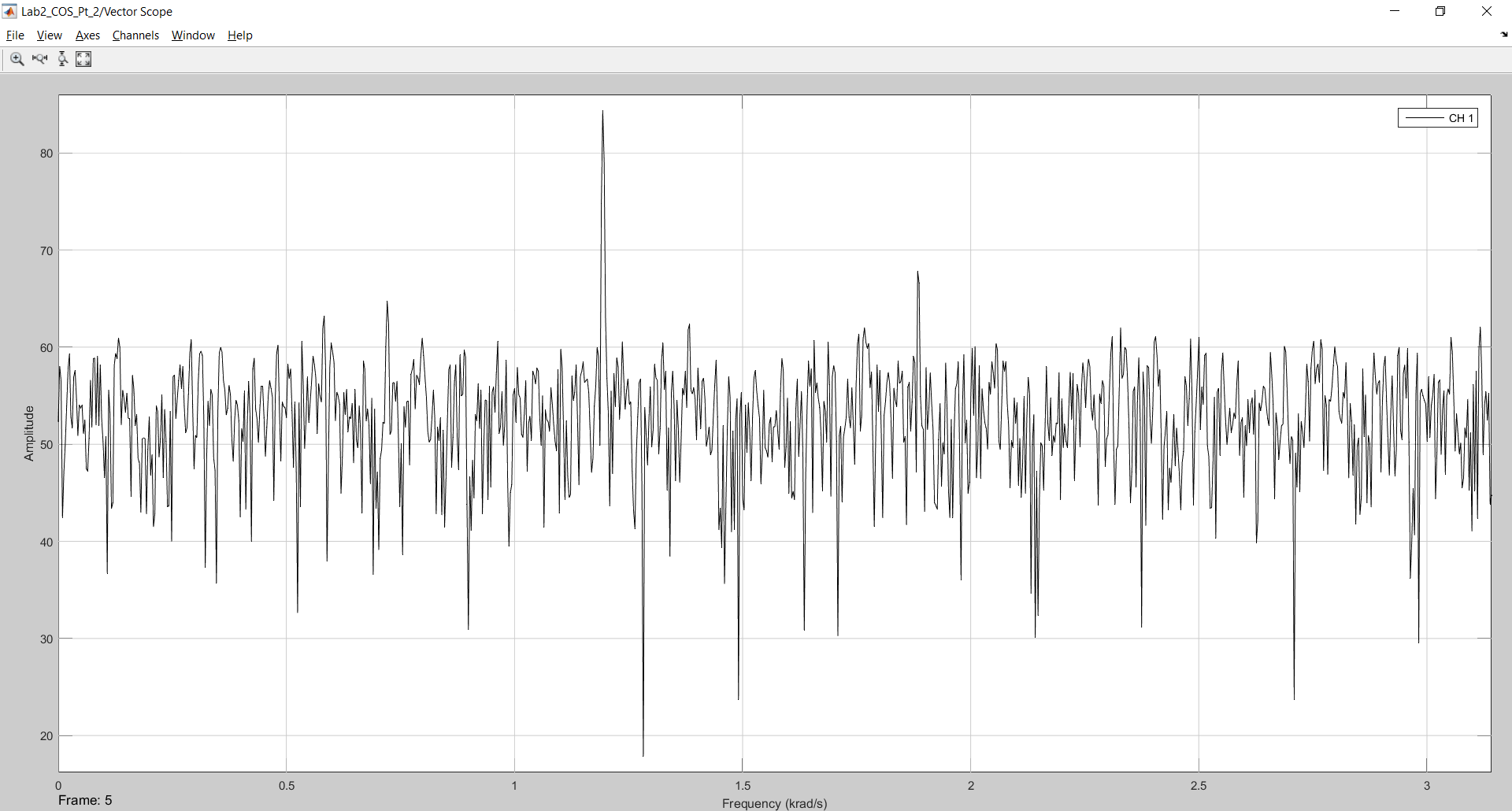
Рисунок 13 – Результат моделирования с генератором шума мощностью 0,4 и количеством отсчетов 2048.
На рисунке 13 уже проблематично найти спектр третьего сигнала, так как некоторые гармоники шума практически сопоставимы с мощностью спектра третьего сигнала. Очевидно, что при повышении мощности шума еще в 2 раза третий спектр станет невидимым в шуме.
Вывод: в данной лабораторной работе изучили влияние сглаживающих окон на спектр сигнала, изучили влияние количества отсчетов на спектр, а также влияние шума. Выполнили сравнительный анализ с приведенными теоретическими данными.