Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Саратовский государственный технический университет имени Гагарина Ю.А.»

Институт Урбанистики, архитектуры и строительства

Кафедра «Теплогазоснабжение и нефтегазовое дело»


Контрольная работа по дисциплине:

«Механика жидкости и газа»

Выполнил: студент 3 курса, группы бМНСТипу-31

Никитин Дмитрий Викторович/ Ф.И.О.

номер зачётной книжки: 200790

Принял: доцент кафедры ТНД

_______________/ Наумова О.В.

Оценка __________ « ____ » ______________ 202_ г.

Саратов 2023 г.

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Саратовский государственный технический университет

имени Гагарина Ю.А.»
Институт Урбанистики, архитектуры и строительства
Кафедра «Теплогазоснабжение и нефтегазовое дело»
ЗАДАНИЕ

на контрольную работу по дисциплине «Механика жидкости и газа»

Студенту учебной группы бМНСТипу -31 Никитину Дмитрию Викторовичу

Вариант 10

1. 
   Что понимают под вязкостью жидкости? Как связаны кинематическая и динамическая вязкость?.
   
2. 
   Какие потери возникают при движении жидкости по трубопроводам? Как они определяются?
   
3. 
   Наклонный трубопровод состоит из двух частей, диаметром d1 = 200 мм и d₂ = 450 мм. Р₁ = 50000 Па, расход воды Q = 0,35 м³/с. Определить скорость движения жидкости в обоих сечения и давление во втором сечении, Z₁ = 5м, Z₂ = 3м. Потерями пренебречь.
   
4. 
   На трубопроводе установлены две задвижки, имеющие коэффициент местного сопротивления ζ₁ = 0,5, коэффициент местного сопротивления на входе в трубопровод составляют ζ₂ = 1, коэффициент местного сопротивления на выходе из трубопровода составляют ζ₂ = 0,7. Длина трубопровода l = 5 км, диаметр d = 0,5м. Расход воды равен Q = 0,1 м³/с, относительная плотность δ = 0,85, Р₁ = 200кПа. Определить потери давления в трубопроводе.
   
5. 
   Два горизонтальных цилиндрических трубопровода А и В содержат соответственно минеральное масло, плотностью 900 кг/м³ и воду, плотностью 1000 кг/м³. Высоты жидкостей h_м = 0,2м, h_рт = 0,4м, h_в = 0,9м.Зная, что гидростатическое давление в трубопроводе на оси А равно 0,6х10⁵Па, определить давление на оси трубопровода В.
   

---

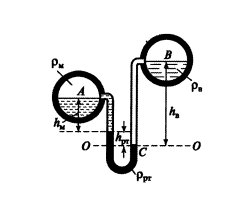
Задание выдал: Задание получил:
доцент кафедры ТНД______ Наумова О.В. студент Никитин Д.В.
дата_________ дата_________

1. Что понимают под вязкостью жидкости? Как связаны кинематическая и динамическая вязкость?

Вязкость (внутреннее трение) – свойство жидкостей оказывать сопротивление действию внешних сил, вызывающих их течение. Это свойство противоположное текучести. Все реальные жидкости обладают определенной вязкостью. Более вязкие: глицерин, масла; менее вязкие – вода. По сравнению с жидкостями газы обладают значительной текучестью, а, следовательно, и малой вязкостью. Гидромеханика изучает движение так называемых ньютоновских жидкостей для которых напряжение, выражаемое силами вязкости выражается линейно через скорости деформаций. Для неньютоновских жидкостей эти законы значительно сложней. Сопротивление таких жидкостей при относительном перемещении слоев не отвечает гипотезе Ньютона и характеризуется наличием эффективной вязкости (жидкость приходит в движение после преодоления некоторого касательного напряжения, имеющегося в состоянии покоя). К таким жидкостям относятся краски, суспензии, коллоидные растворы, смолы и др. Поведение таких жидкостей изучает реология.

Известны два вида вязкости жидкости: объемная и тангенциальная.

Наличие сил вязкостного трения в движущейся жидкости подтверждается простым и наглядным опытом. Если в цилиндрическую ёмкость, заполненную жидкостью опустить вращающийся цилиндр, то вскоре придёт в движение (начнёт вращаться вокруг своей оси в том же направлении, что и вращающийся цилиндр) и сама ёмкость с жидкостью. Этот факт свидетельствует о том, что вращательный момент от вращающегося цилиндра был передан через вязкую жидкость самой ёмкости, заполненной жидкостью.

Напряжения, возникающие при деформации сдвига согласно гипотезе Ньютона про­порциональны градиенту скорости в движущихся слоях жидкости, а сила трения между слоями движущейся жидкости будет пропорциональна площади поверхности движущихся слоев жидкости:

---

где Т - сила трения между слоями движущейся жидкости,

S - площадь поверхности слоев движущейся жидкости,

τ - касательные напряжения, возникающие в жидкости при де­формации сдвига,



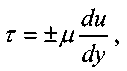
μ - коэффициент динамической вязкости жидкости.

Величина коэффициента динамической вязкости жидкости при постоянной темпера­туре и постоянном давлении зависит от внутренних (химических) свойств самой жидко­сти.

Помимо коэффициента динамической вязкости жидкости широко используется ко­эффициент кинематической вязкости жидкости v, представляющий собой отношение ко­эффициента динамической вязкости к плотности жидкости:



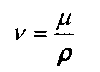
В системе единиц СИ коэффициент кинематической вязкости измеряется в м /с, в системе единиц СГС единицей измерения коэффициента кинематической вязкости жидко­сти является стоке (cm), т.е. 1 cm = 1 см /с.

Вязкость жидкости в значительной степени зависит от температуры и давления. При увеличении температуры капельной жидкости коэффициенты её вязкости (как динамиче­ский, так и кинематический) резко снижается в десятки и сотни раз, что обусловлено уве­личением внутренней энергии молекул жидкости по сравнению с энергией межмолеку­лярной связи в жидкости.

2. Какие потери возникают при движении жидкости по трубопроводам? Как они определяются?

При движении жидкости ее энергия уменьшается за счет потерь на преодоление сопротивлений. Различают потери напора по длине и местные потери напора. Потери напора по длине определяются по формуле Дарси-Вейсбаха:



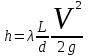
где - коэффициент гидравлического трения; L - длина трубопровода; V - скорость движения воды; d - диаметр трубопровода; g - ускорение свободного падения. Потери напора по длине в значительной степени зависят от режима движения.

Критерий Рейнольдса, который определяет режим движения можно найти по формуле:

Re =

---

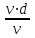
При значении Re < 2320 движение в потоке относят к ламинарному (струйному), в противном случае говорят о турбулентном движении (вихревом). При ламинарном движении Re.

При турбулентном движении формулу для определения коэффициента гидравлического трения определяют в зависимости от значения следующего критерия:

К = Re* ,

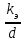k_э – эквивалентная шероховатость, мм.

При значении К > 500 коэффициент гидравлического трения определяют по формуле Шифринсона:

  

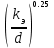
При К < 10 коэффициент гидравлического трения определяют по формуле Блазиуса:

  0.316/Re ^0.25

При 10 < К < 500 коэффициент гидравлического трения определяют по формуле Альтшуля:



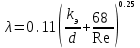
Для определения потерь напора по длине определяют скорость течения, величину Re, а затем величину К и по ее значению выбирают формулу для определения коэффициента гидравлического трения. Формула Альтшуля применима при любых значениях К, поэтому эту формулу можно использовать всегда.

Потери напора в арматуре (задвижка, вентиль, кран и др.), при изменении направления движения потока воды, при соединении или разделении потоков, при сужении или расширении сечения трубы (канала), при поворотах называют местными.

Местные потери напора определяют по формуле:



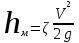
ζ - коэффициент местного сопротивления, определяется по справочным данным в учебниках или справочниках. Порядок определения местных сопротивлений: определяют скорость течения воды в трубопроводе или канале, как правило, после сопротивления (поворот, сужение, расширение трубопровода или канала), по значению отношения площади сечения или угла поворота определяют значение коэффициента местных сопротивлений, а затем подсчитывают величину местного сопротивления.

---

Потери напора по длине и местные сопротивления определяются в метрах водного столба.

Гидравлически длинными трубопроводами называют трубопроводы, в которых местные сопротивления малы по сравнению с потерями по длине, в этих трубопроводах местные сопротивления принимают в пределах 10-20% от потерь напора по длине.

В гидравлически коротких трубопроводах местные сопротивления сравнимы по величине с местными потерями напора и в этих трубопроводах общие потери напора определяют по формуле:

H = h_м + h_дл
3. Наклонный трубопровод состоит из двух частей, диаметром d₁ = 200 мм и d₂ = 450 мм. Р₁ = 50000 Па, расход воды Q = 0,35 м³/с. Определить скорость движения жидкости в обоих сечения и давление во втором сечении, Z₁ = 5м, Z₂ = 3м. Потерями пренебречь.
Дано: d₁ = 200 мм=0,2 м, d₂ = 450 мм=0,45 м, Р₁ = 50000 Па,
Q = 0,35 м³/с, Z₁ = 5м, Z₂ = 3м

Найти V₁, V₂, p₂

Решение:

Скорость в трубопроводе:



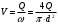
Скорости на участках:





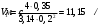
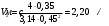
Составим уравнение Бернулли для идеальной жидкости:



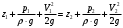
Скорость в сечении 2-2:

4. 
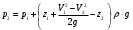
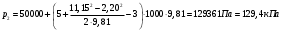
   На трубопроводе установлены две задвижки, имеющие коэффициент местного сопротивления ζ₁ = 0,5, коэффициент местного сопротивления на входе в трубопровод составляют ζ₂ = 1, коэффициент местного сопротивления на выходе из трубопровода составляют ζ₂ = 0,7. Длина трубопровода l = 5 км, диаметр d = 0,5м. Расход воды равен Q = 0,1 м³/с, относительная плотность δ = 0,85, Р₁ = 200кПа. Определить потери давления в трубопроводе.
   

Дано: ζ₁ = 0,5, ζ₂ = 1, ζ₃ = 0,7, l = 5 км=5000 м, d = 0,5м, Q = 0,1 м³/с, δ = 0,85, Р₁ = 200кПа=200000 Па

Найти ∆р

Решение:

Скорость в трубопроводе:





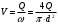
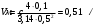
Общие потери напора определяют по формуле:

H =

---

Смотрите также файлы

• Задача получение.docx

• Тесты цикла по специальности Стоматология терапевтическая.docx

• К. Д. Ушинского Добротиной Анны Александровны.docx

• Задача 1 Оценка риска.docx

• Создание электронной книги. Относительная и абсолютная адресации в ms excel.docx