МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО

ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН

СОВЕСТНАЫ МЕЖДУНАРОДНАЯ

ОБРАЗОВАТЕЛЬНАЯ ПРОГРАММА

КОНТРОЛЬНАЯ РАБОТА

ПО ДИСЦИПЛИНЕ

Эконметрика

Студент (Ф.И.О.) Толибова Фотиманисо Мухтор-кизи

Группа: КЭ-12

1. Корректное формирование модели регрессии.

Статистическая функция ЛИНЕЙН определяет параметры линейной регрессии у=ах+b. Порядок вычисления следующий:

1) введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2) выделите область пустых ячеек 52 (5 строк, 2 столбца) длявывода результатов регрессионной статистики или область 12 – для получения только оценок коэффициентов регрессии;

3) активизируйте Мастер функций любым из способов:

а) в главном меню выберите Вставка/Функция;

б) на панели инструментов Стандартная щелкните по кнопке Вставка функции;

4) в окне Категория выберите Статистические, в окне Функция – ЛИНЕЙН. Щелкните по кнопке ОК;

5) заполните аргументы функции:

Известные_значения_у – диапазон, содержащий данные резуль­тативного признака;

Известные_значения_х – диапазон, содержащий данные факто­ров независимого признака;

Константа - логическое значение, которое указывает на нали­чие или на отсутствие свободного члена в уравнении; если Кон­станта = 1, то свободный член рассчитывается обычным обра­зом, если Константа = 0, то свободный член равен 0;

Статистика – логическое значение, которое указывает, выво­дить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.

Щелкните по кнопке ОК;

6) в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите клавишу , а затем – на комбинацию клавиш ++.

Регрессионная статистика представляется в выделенной области в следующем порядке:

Значение коэффициента a	Значение коэффициента b
Среднеквадратическое отклонение a	Среднеквадратическое отклонение b
Коэффициент детерминации R2	Среднеквадратическое отклонение y
F-статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

2.5.2. Многофакторная регрессия.

Построение линейной многофакторной модели производится с помощью инструментов пакета анализа данных Корреляция и Регрессия. Корреляция используется для расчета матрицы парных коэффициентов корреляции. С помощью Регрессии, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:

1. 
   проверьте доступ к пакету анализа. В главном меню последовательно выберите Сервис/Надстройки. Установите флажок Пакет анализа;
   
2. 
   введите исходные данные или откройте существующий файл, содержащий анализируемые данные;
   
3. 
   в главном меню выберите пункты Сервис/Анализ данных/ Корреляция;
   
4. 
   заполните диалоговое окно входных данных и параметров вывода:
   

Входной интервал – диапазон, содержащий анализируемые данные (все столбцы или строки);

Группирование – по столбцам или по строкам;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Выходной интервал – достаточно указать левую верхнюю ячейку диапазона;

5. 
   результаты вычислений – матрица парных коэффициентов корреляции, анализ которых позволяет выполнить первый этап процесса моделирования, описанный в 2.4;
   
6. 
   в главном меню выберите пункты Сервис/Анализ данных/ Регрессия;
   
7. 
   заполните диалоговое окно входных данных и параметров вывода как в пункте 4, только интервал для результативного признака Y и для факторов Х надо задавать отдельно (причем входной интервал Х должен включать все столбцы, содержащие значения факторных признаков);
   
8. 
   в результате получаем регрессионную статистику, таблицу дисперсионного анализа и таблицу коэффициентов модели, в которой первая строка (Y-пересечение) соответствует коэффициенту а₀, а следующие строки описывают коэффициенты регрессии а_i.
   

6. 
   Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками.
   

Итак, при исследовании остатков _i должно проверяться наличие следующих пяти предпосылок МНК:

1. 
   случайный характер остатков;
   
2. 
   нулевая средняя величина остатков, не зависящая от х_i;
   
3. 
   гомоскедастичность – дисперсия каждого отклонения_iодинакова для всех значенийх_i;
   
4. 
   отсутствие автокорреляции остатков – значения остатков_iраспределены независимо друг от друга;
   
5. 
   остатки подчиняются нормальному распределению.
   

Если распределение случайных остатков _iне соответствует некоторым предпосылкам МНК, то следует корректировать модель.

В случае нарушения первых двух предпосылок необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии.

Пятая предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t,F. Однако и при нарушении пятой предпосылки МНК оценки регрессии обладают достаточной состоятельностью.

Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение третьей и четвертой предпосылок.

Если не соблюдается гомоскедастичность, то имеет место гетероскедастичность. Наличие гетероскедастичности может привести к смещенности оценок коэффициентов регрессии, а также к уменьшению их эффективности. В этом случае рекомендуется применятьобобщенный метод наименьших квадратов, который заключается в том, что при минимизации суммы квадратов отклонений (5) отдельные ее слагаемые взвешиваются: наблюдениям с большей дисперсией придается пропорционально меньший вес. Чтобы убедиться в гетероскедастичности остатков и, следовательно, в необходимости использования обобщенного МНК, обычно не ограничиваются визуальной проверкой гетероскедастичности, а проводят ее эмпирическое подтверждение, в частности, используют метод Гольдфельда – Квандта. Проиллюстрируем его на примере (табл.7).

Таблица 7.

Поступления налогов в бюджет (y_i– млн.руб.) в зависимости

от численности работающих (х_i– тыс.чел).

№ п/п	хi	yi	ŷх	i
1	2	3	4	5
1	3	4,4	-1,0	5,4
2	6	8,1	2,5	5,6
3	8	12,9	4,9	8,0
4	18	20,8	16,6	4,2
5	20	15,5	19,0	-3,5
6	23	28,8	22,5	6,3
7	39	37,5	41,4	-3,9
8	49	48,7	53,2	-4,5
9	60	68,6	66,1	2,5
10	74	104,6	82,6	22,0
11	79	90,5	88,5	2,0
12	95	88,3	107,4	-19,1
13	106	132,4	120,4	12,0
14	112	122,0	127,4	-5,4
15	115	99,1	131,0	-31,9
16	125	114,2	142,7	-28,5
17	132	150,6	151,0	-0,4
18	149	156,1	171,0	-14,9
19	157	209,5	180,5	29,0
20	282	342,9	327,8	15,1
итого	1652	1855,5	1855,5	0,0

По выборочным данным строим уравнение регрессии

ŷ_х= –4,565 + 1,178х.

Теоретические значения ŷ_х и отклонения от них фактических значений_iприведены в четвертой и пятой колонке табл.7. Очевидно, что остаточные величины_iобнаруживают тенденцию к росту по мере увеличенияхиу. Этот вывод подтверждается и по критерию Гольдфельда – Квандта. Для его применения необходимо выполнить следующие шаги:

• 
  упорядочить nнаблюдений по мере возрастания переменнойх (выполнено);
  
• 
  исключить из рассмотрения kцентральных наблюдений (рекомендовано приn=60 приниматьk=16, приn=30 приниматьk=8, приn=20 приниматьk=4), в данном случае исключаем строки 9–12;
  
• 
  разделить совокупность на две группы (по ń=(n–k):2=8 наблюдений соответственно с малыми и большими значениями факторах) и определить по каждой из групп уравнения регрессии (результаты в табл.8.);
  
• 
  определить остаточные суммы квадратов для первой (S₁) и второй (S₂) групп и найти их отношениеR=S₂:S₁. Чем больше величинаRпревышает табличное значениеF–критерия с ń –2 степенями свободы (приложение 2), тем более нарушена предпосылка о равенстве дисперсий остаточных величин, т.е. наблюдается гетероскедастичность остатков.
  

Таблица 8.

№ п/п	хi	yi	ŷх	i	i2
1	3	4,4	5,7	–1,3	1,69
2	6	8,1	8,5	–0,4	0,16
3	8	12,9	10,3	2,6	6,76
4	18	20,8	19,6	1,2	1,44
5	20	15,5	21,4	–5,9	34,81
6	23	28,8	24,2	4,6	21,16
7	39	37,5	38,9	–1,4	1,96
8	49	48,7	48,1	0,6	0,36
Уравнение регрессии: ŷх = 2,978 + 0,921х. Сумма S1=68,34
13	106	132,4	110,7	21,7	470,89
14	112	122,0	118,7	3,3	10,89
15	115	99,1	122,7	–23,6	556,96
16	125	114,2	136,1	–21,9	479,61
17	132	150,6	145,4	5,2	27,04
18	149	156,1	168,2	–12,1	146,41
19	157	209,5	178,9	30,6	936,36
20	282	342,9	346,1	–3,2	10,24
Уравнение регрессии: ŷх = 31,142 + 1,338х. СуммаS2 =2638,4

Величина R=2638,4 : 68,34=38.6 существенно превышает табличное значениеF-критерия 4,28 при 5%-ном и 8,47 при 1%-ном уровне значимости для числа степеней свободы 8 – 2 = 6, подтверждая тем самым наличие гетероскедастичности.

Нарушение четвертой предпосылки МНК – автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Коэффициент корреляции r_ijмежду_iи_j, где_i– остатки текущих наблюдений,_j– остатки предыдущих наблюдений (например,j=i–1) определяется по обычной формуле линейного коэффициента корреляции (2).

Для подсчета автокорреляции необходимо наблюдения упорядочить по значению фактора х (как в предыдущем примере) и составить ряды с текущими и предыдущими остатками. Рассмотрим расчет коэффициента корреляции между_iи_j, взяв в качестве примера данные из табл.7 и перенеся их в табл. 9 (n=19).

Таблица 9.

№ п/п	i	i-1	ii-1
1	5,6	5,4	30.24
2	8,0	5,6	44.8
3	4,2	8,0	33.6
4	–3,5	4,2	–14.7
5	6,3	–3,5	–22.05
6	–3,9	6,3	–24.57
7	–4,5	–3,9	17.55
8	2,5	–4,5	–11.25
9	22,0	2,5	55
10	2,0	22,0	44
11	–19,1	2,0	–38.2
12	12,0	–19,1	–229.2
13	–5,4	12,0	–64.8
14	–31,9	–5,4	172.26
15	–28,5	–31,9	909.15
16	–0,4	–28,5	11.4
17	–14,9	–0,4	5.96
18	29,0	–14,9	–432.1
19	15,1	29,0	435
итого	–5.3998	–15.1031	922.09
среднее	–0,2842	–0,7949	48.5311

σ_i=15.1347, σ_j=14,7663 и в соответствие с (2)

r_ij=(48,5311 – (–0,2842)(–0,7949))/15,1347/14,7663=0,2161,

что при 17 степенях свободы явно незначимо и демонстрирует отсутствие автокорреляции остатков.

Автокорреляция остатков может быть вызвана несколькими причинами, имеющими различную природу. Во-первых, иногда она связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака. Во-вторых, причину следует искать в формулировке модели, которая может не включать существенный фактор, влияние которого отражается в остатках, вследствие чего они оказываются автокоррелированными. Очень часто этим фактором является фактор времени, поэтому проблема автокорреляции остатков весьма актуальна при исследовании динамических рядов, что мы рассмотрим в соответствующем разделе.

---

2. Практическая реализация решения модели парной линейной регрессии в Excel

Уравнение линейной парной регрессии имеет вид:

  

где   — моделируемая переменная,
 — переменная-фактор,
 — ошибка.

Стандартной задачей является нахождение параметров   и   для конкретных статистических данных. Рассмотрим пример решения этой задачи простыми инструментами программы MS Excel.

Пример. Изучается зависимость себестоимости единицы изделия ( , тыс. руб.) от величины выпуска продукции ( , тыс. шт.) по группам предприятий за отчетный период. Экономист обследовал   предприятий и получил следующие результаты:

	2	3	4	5	6
	1,9	1,7	1,8	1,6	1,4

Найти уравнение линейной парной регрессии   .

Источник: Просветов Г.И. Эконометрика: задачи и решения: учебно-методическое пособие. — М.: Издательство «Альфа-пресс», 2008. — 192 с. (Пример 18, с.32)

Решение. Введем исходные данные в таблице MS Excel:



Выделим диапазон исходных данных:

---

В меню Вставка выбираем инструмент Точечная диаграмма (именно эта диаграмма позволяет строить точки по двум координатам):



Появляется диаграмма (в статистике этот график называют корреляционным полем):



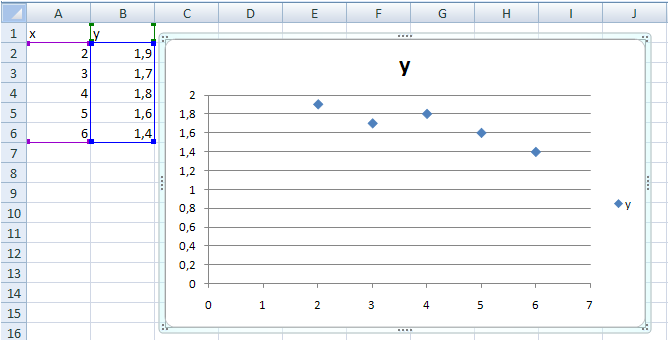
Выполняем правый щелчок мыши по любой точке на диаграмме, появляется контекстное меню, в котором выбираем команду Добавить линию тренда:



Появляется окно диалога:



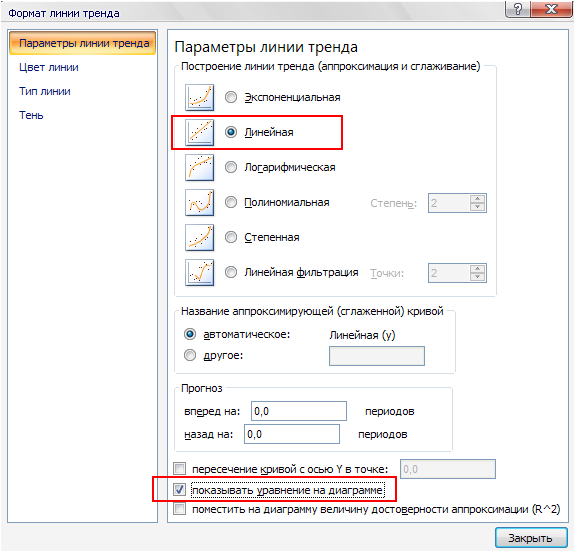
В окне диалога Формат линии тренда выбираем вид Линейная (обычно выбрано по умолчанию) и ставим флажок Показывать уравнение на диаграмме, нажимаем кнопку Закрыть. На точечной диаграмме появляется сглаживающая линия и ее уравнение, это и есть искомое уравнение регрессии:



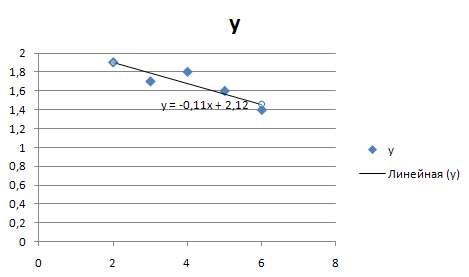
Таким образом, уравнение регрессии имеет вид:

  

Сделаем вывод: коэффициент регрессии   показывает, что при увеличении выпуска продукции на одну тысячу штук, себестоимость единицы продукции уменьшается в среднем на 0,11 тысяч рублей.

Задание на СР: Найти уравнение линейной парной регрессии, если    — недельные объемы продаж, тыс. руб.,   — расходы на рекламу, тыс. руб.

	5	8	6	5	3	9	12	4	3	10
	72	76	78	70	68	80	82	65	62	90

---

3. Анализ полученного решения и экономическая интерпретация результатов

Любая экономико-математическая модель лишь упрощенно, грубо отображает реальный экономический процесс, и это упроще­ние существенно сказывается на получаемых результатах. Исследователя вряд ли устроила бы заключительная симплекс-таблица, из которой можно было бы получить только список переменных и их значения. На самом же деле результирующая симплекс-таблица «насыщена» весьма важными данными, лишь небольшую часть ко­торых составляют оптимальные значения переменных. Из симп­лекс-таблицы можно получить информацию относительно:

• 
  оптимального решения;
  
• 
  статуса ресурсов;
  
• 
  ценности каждого ресурса;
  
• 
  чувствительности оптимального решения к изменению запасов ресурсов, вариациям коэффициентов целевой функции и интен­сивности потребления ресурсов.
  

Сведения, относящиеся к первым трем пунктам, можно извлечь непосредственно из итоговой симплекс-таблицы. Получение ин­формации, относящейся к четвертому пункту, требует дополни­тельных вычислений.

Для иллюстрации возможностей получения указанной выше информации из заключительной симплекс-таблицы воспользуемся опять задачей об ассортименте продукции (пример 7.2). Эта задача формулируется следующим образом:

максимизировать:   (доход);

при следующих ограничениях:   (сырьё А),

 (сырьё В),

 (спрос),

 (спрос).

Оптимальная симплекс – таблица имеет вид:

Свободные неиз-вестные Базисные неизвестные	Свободный Член	y1	y3
x1	2.4	0.2	0.6
y2	3	-1	-1
y4	0.6	-0.2	0.4
x2	1.4	0.2	-0.4
Zmax	12.8	1.4	0.2

---

В таблице   - выравнивающие переменные.

Оптимальное решение

С точки зрения практического использования результатов ре­шения задач линейного программирования классификация пере­менных на базисные и небазисные не имеет значения и при анали­зе оптимального решения может не учитываться. Переменные, от­сутствующие в симплекс-таблице в столбце «базисные перемен­ные», обязательно имеют нулевое значение. Значения остальных переменных приводятся в столбце «свободные члены».

При интерпретации результатов оптимизации в задаче об ас­сортименте продукции нас прежде всего интересуют объемы про­изводства продукции П₁ и П₂, т. е. значения управляемых перемен­ных x₁ и х₂- Используя данные, содержащиеся в симплекс-таблице для оптимального решения, основные результаты можно предста­вить в следующем виде:

Управляемые переменные	Оптимальные значения	Решение
x1 х2	2,4 1,4	Объем производства продук­ции П1, должен быть равен 2,4 ед. в сутки Объем производства продук­ции П2должен быть равен 1,4 ед. в сутки
Zmax	12,8	Доход от реализации продукции будет равен 12,8 д. е. в сутки

Статус ресурсов

В п. 7.4 ресурсы относились либо к дефицитным либо к неде­фицитным — в зависимости от того, полное или частичное их ис­пользование предусматривает оптимальное решение задачи. Сейчас цель состоит в том, чтобы получить соответствующую информа­цию непосредственно из оптимальной таблицы.

В модели, построенной для задачи об ассортименте продукции, фигурируют четыре ограничения со знаком « ». Первые два огра­ничения (определяющие допустимый расход исходного сырья) представляют собой истинные ограничения на ресурсы. Третье и четвертое ограничения относятся к спросу. Эти требования можно рассматривать как ограничения на соответствующие ресурсы, так как увеличение спроса на продукцию эквивалентно расширению представительства предприятия на рынке сбыта. В отношении финансовых средств такая ситуация имеет те же последствия, что и

---

Смотрите также файлы

• Контрольная работа по дисциплине Кадровая политика и управление персоналом в правоохранительных органах.docx

• Влияние природных факторов на здоровье.docx

• Лизингвид предпринимательской деятельности по инвестированию средств в коммерческих организациях.doc

• Реферативная работа Содержание.docx

• 23 мм Укажите, какую ширину должна иметь дуга каркаса бюгельного протеза на верхней челюсти Ответ 58 мм.docx